3 Herramientas de análisis
Una vez se tiene sistematizada y cuantificada la realidad social que se quiere investigar en un marco de datos, el análisis cuantitativo permite generar conocimiento de estos fenómenos a través de técnicas estadísticas. Principalmente, la estadística ofrece dos maneras de generar conocimiento: la estadística descriptiva y la estadística inferencial.
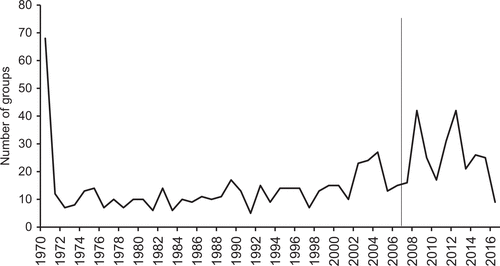
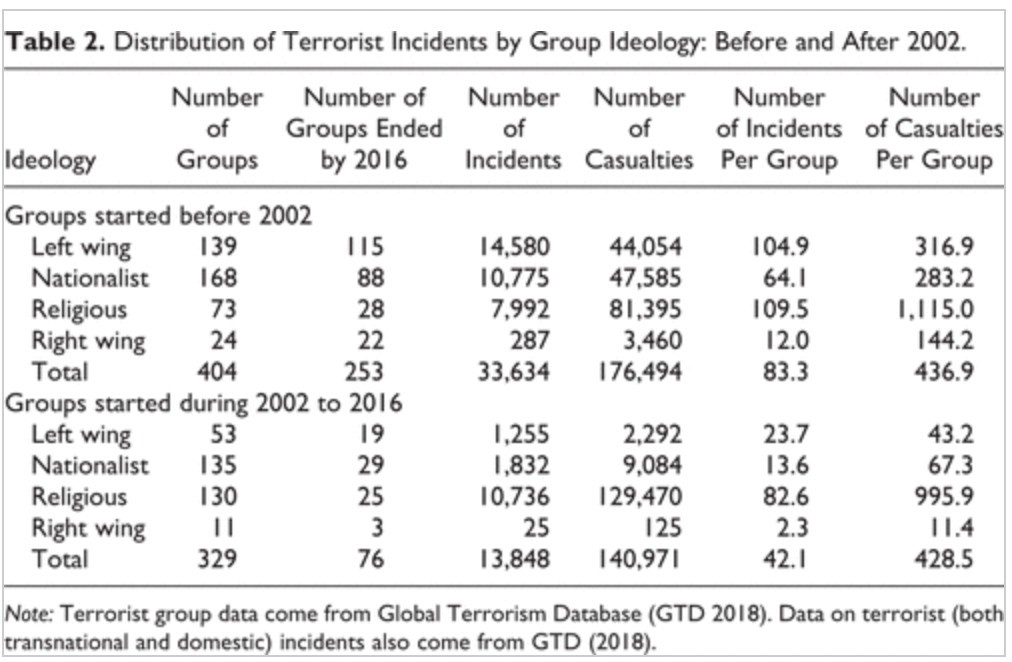
La estadística descriptiva nos permite resumir volúmenes grandes de datos de manera numérica y visual. Hou et al. (2019) recogieron datos de grupos terroristas entre 1970 y 2016, con los que pudieron generar descriptivos como la evolución del número anual de grupos terroristas nuevos (Figura 3.1 (a), izquierda) y la distribución de incidentes terroristas segundos la ideología del grupo terrorista y de si el grupo terrorista se formó antes o después del año 2002 (Figura 3.1 (b), derecha). Con las técnicas de la estadística descriptiva los autores pudieron generar resúmenes de los datos, sobre los cuales pudieron observar que se estaba produciendo una variabilidad en la formación de grupos terroristas a partir de 2007 y que los grupos terroristas de izquierda habían tenido más influencia en el número de incidentes terroristas entre 1970 y 2001, pero habían causado menos muertos que los grupos religiosos o los nacionalistas.
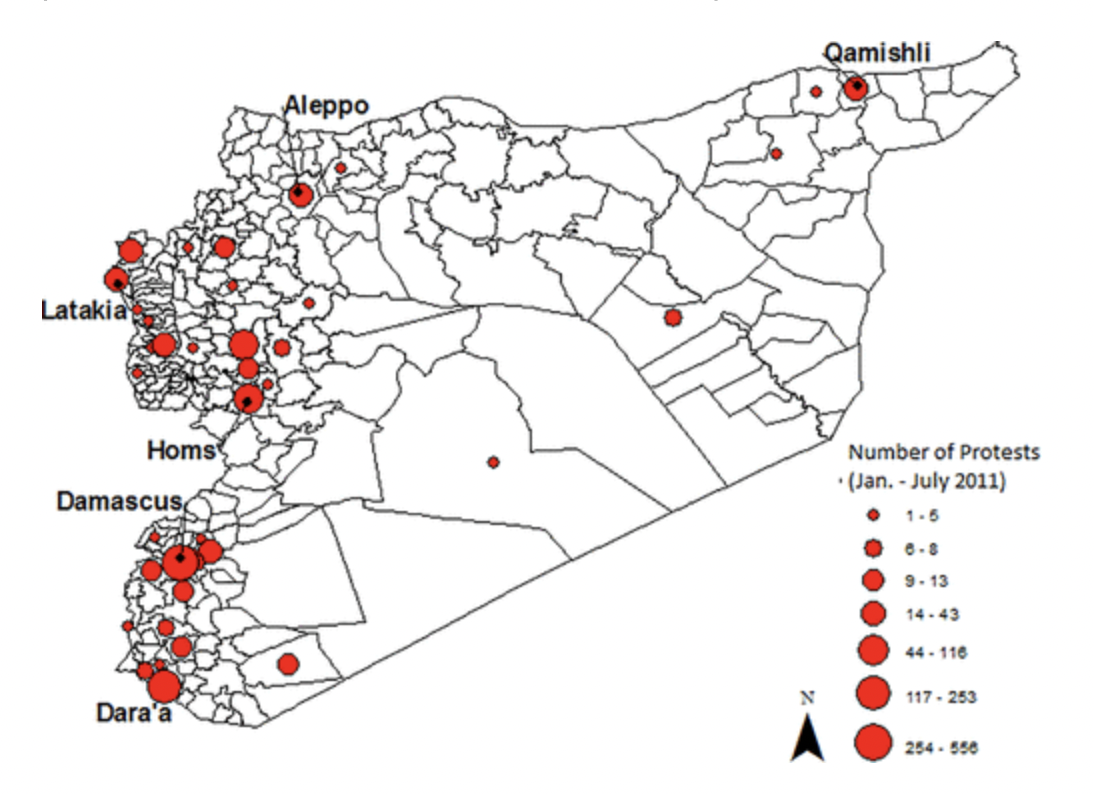
La estadística descriptiva también puede ser útil para generar resúmenes de datos sobre mapas. Ash & Obradovich (2020) construyeron sobre un mapa por distritos de Siria una visualización del número de protestas contra el gobierno sirio entre los meses de enero y julio de 2011. Los datos geolocalizados del mapa que se muestran en la Figura 3.2 provienen de la Integrated Conflict Early Warning System, generados a partir de análisis de textos mediante machine learning en varios medios de comunicación de habla inglesa.
Por otro lado, la estadística inferencial nos permite hacer deducciones sobre una población de casos a partir de una pequeña muestra. La importancia de esta técnica es que nos permite emitir juicios sobre el efecto que tienen algunos fenómenos sobre otros. Por ejemplo, Bakken & Buhaug (2020) estudiaron el potencial transformativo de los conflictos armados, en concreto los efectos que podían tener la resolución del conflicto sobre el empoderamiento femenino. Los autores partían de la intuición que bajo ciertas condiciones los conflictos armados podían suponer una ventana de oportunidad para las mujeres. En los resultados de su análisis cuantitativo hecho en una población de cerca de 6.000 casos, que observamos en la Figura 3.3, encontraron que la severidad del conflicto y su resolución negociada favorecían el empoderamiento femenino.
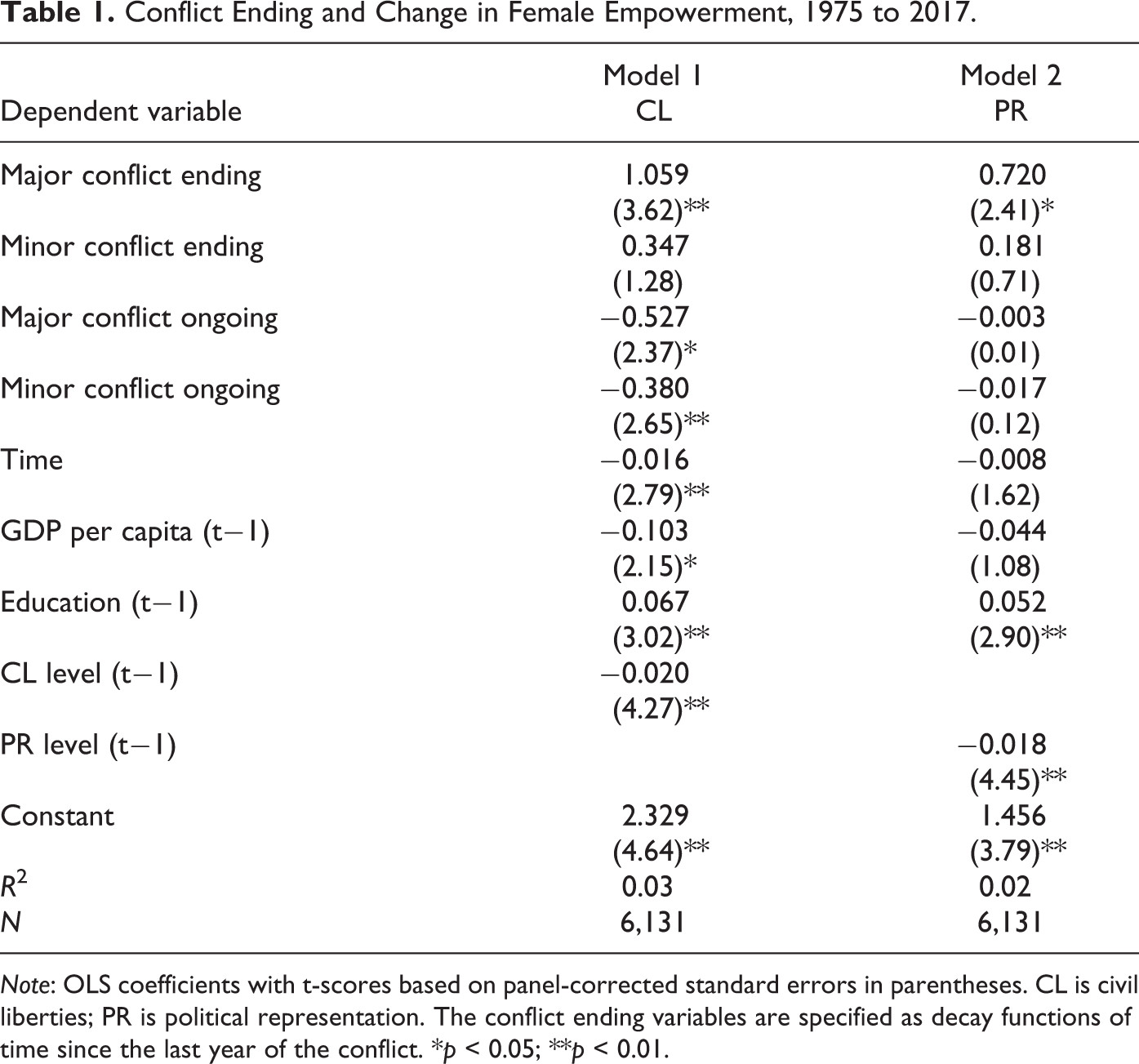
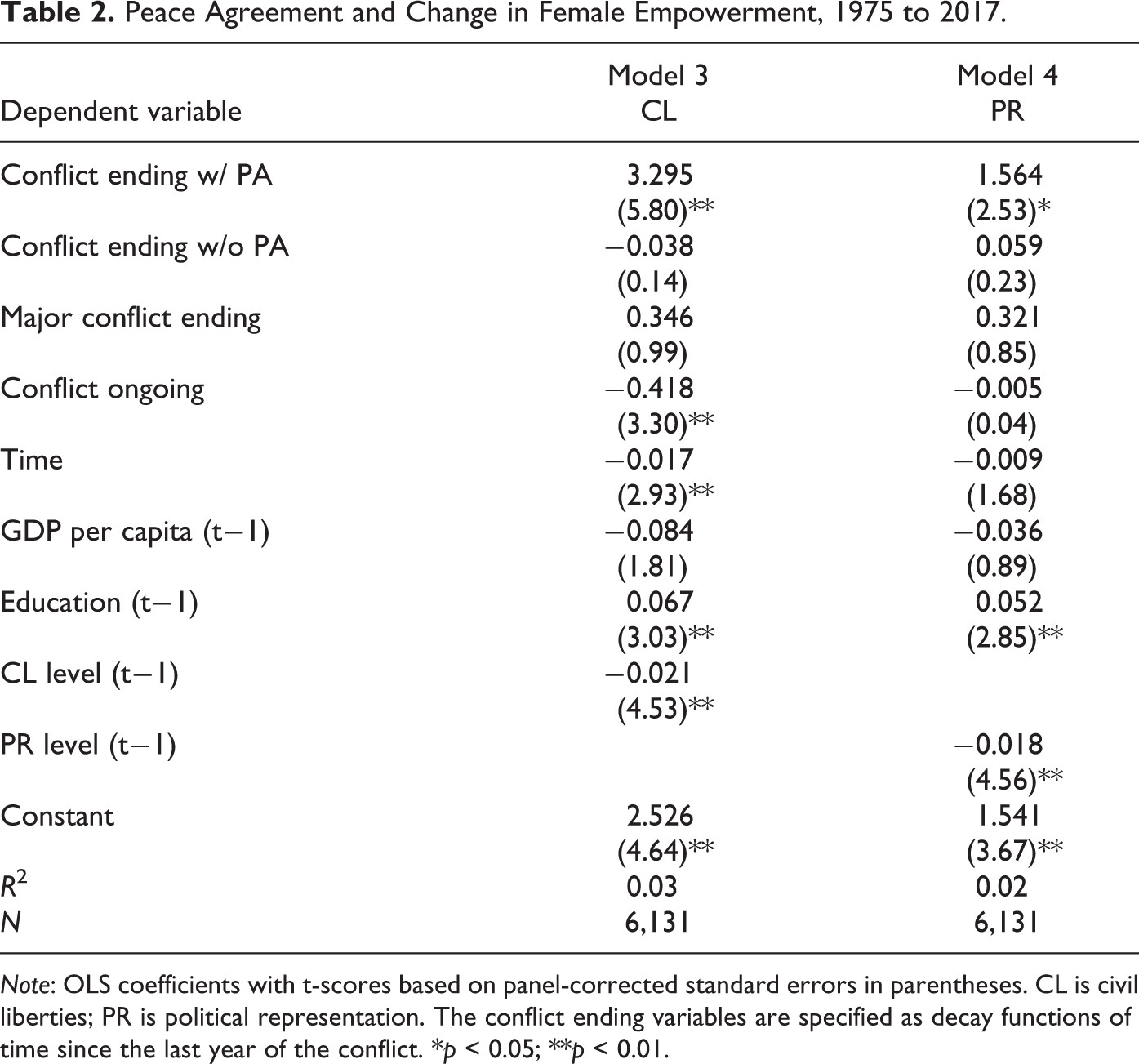
Hasta que no se leen unas cuantas tablas estadísticas, interpretarlas resulta complicado al principio. La regla básica es que las columnas donde aparecen los números son modelos (1, 2, 3 y 4). Los modelos dentro de un mismo estudio acostumbran a tener un solo fenómeno a explicar (en este caso, el cambio en el empoderamiento femenino). En cada modelo se escogen varias variables que compiten entre ellas para explicar el fenómeno y solo las variables que tienen uno o más asteriscos tienen un efecto mínimamente significativo sobre el fenómeno. Por ejemplo, en el modelo 1 vemos que cuando el conflicto que finaliza es considerado mayor (Major Conflict ending) se producen cambios en el empoderamiento femenino en la población afectada (**). En cambio, cuando el conflicto es menor (Minor Conflict ending) no se producen cambios. Una interpretación correcta de estas tablas es más complicada, pero ya lo veremos más adelante.
La estadística inferencial también se puede representar en varios tipos de gráficos. Dancy et al. (2020) quisieron estudiar los determinantes de las opiniones de la población africana sobre el Tribunal Penal Internacional (TPI). Para ello, utilizaron una encuesta a 507 individuos en Kenia y encontraron que las opiniones eran más favorables en la justicia internacional si los encuestados habían sido expuestos a la violencia y más desfavorables si los encuestados pertenecían a los grupos étnicos Kikuyu o Kalenjin, cuyos líderes se habían manifestado reiteradamente en contra del TPI (Figura 3.4).
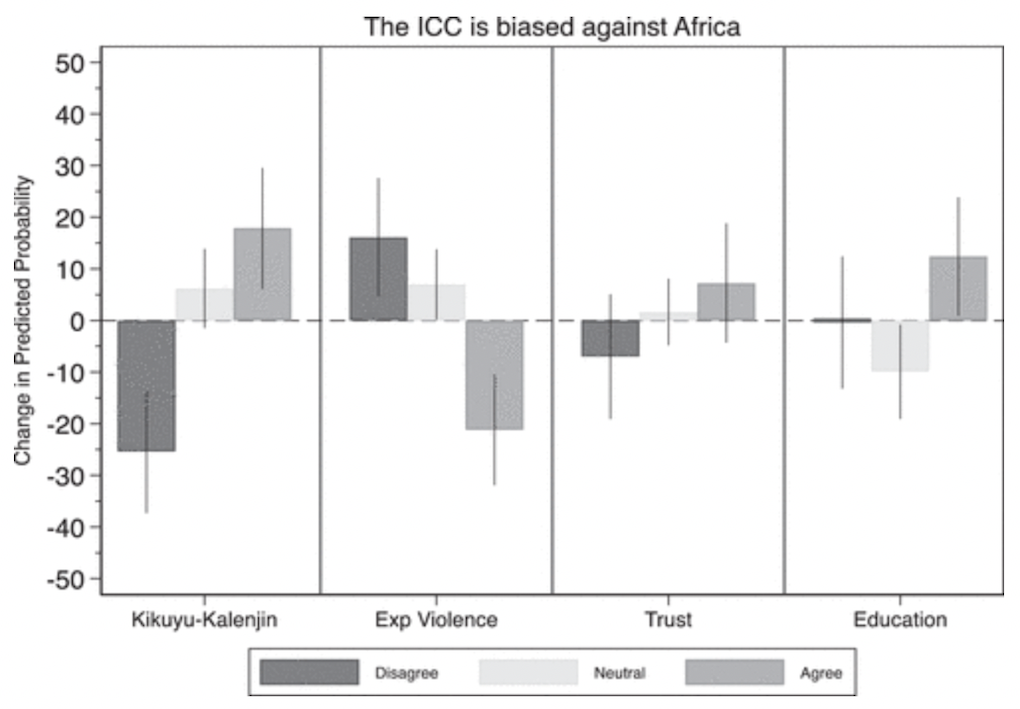
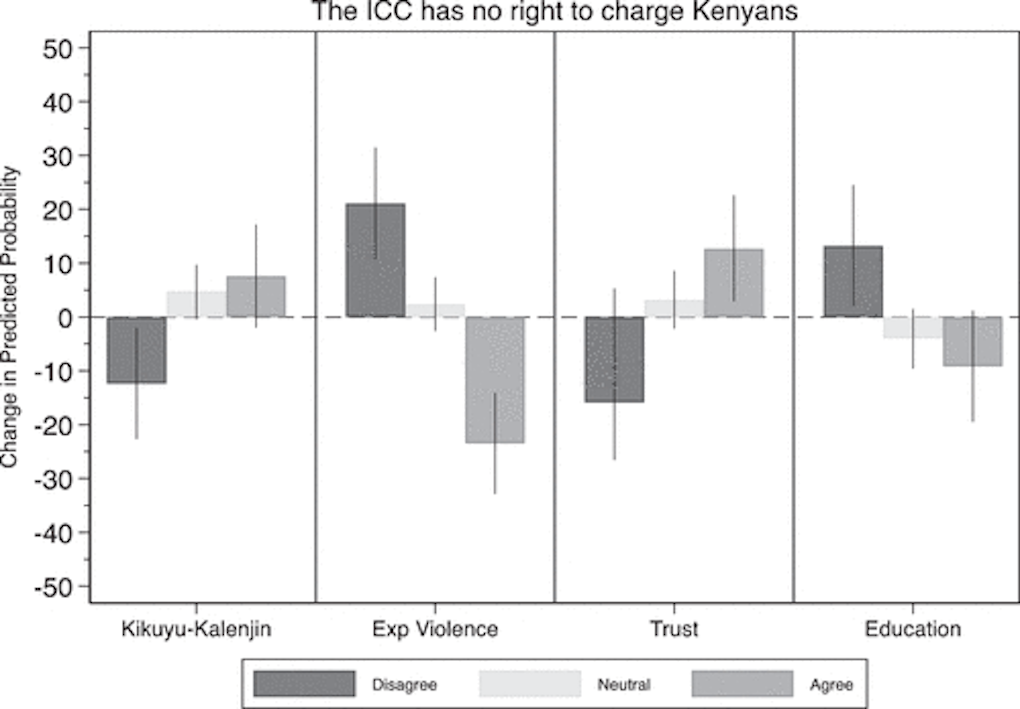
De las anteriores figuras, seguramente podemos sacar dos conclusiones principales. La primera es que el análisis cuantitativo es una técnica fundamental en las RRII. Así lo acreditan las principales revistas especializadas sobre la materia, que exploran el mundo de una manera sistemática y cuantificable. La segunda conclusión es que la interpretación de los resultados producidos por las técnicas de análisis cuantitativo es complicada y requiere un conocimiento especializado que permita interpretar estos análisis. Esto acentúa todavía más la necesidad que alguien que esté interesado en estudiar la realidad internacional sepa utilizar e interpretar no solo marcos de datos, sino también tablas y gráficos estadísticos.