11 Variables
11.1 Introducción
Una variable es una característica del fenómeno que queremos estudiar, que varía entre observaciones y que, por lo tanto, toma varios valores. Si una determinada característica toma el mismo valor en todas las observaciones del marco de datos, entonces no es una variable, simplemente, porque no varía. Volvemos a explorar el marco de datos de elecciones, pero esta vez vemos señalada en rojo una de sus variables en la figura 11.1. La columna turnout es una característica del fenómeno que estamos estudiando, que son las elecciones. Y es, por lo tanto, una variable porque adopta diferentes valores: 54.98, 55.97, etc. El nombre del país también es una característica de cada unidad, puesto que nos indica el nombre del país donde se han producido las elecciones. Todas ellas, si nos fijamos bien, son variables. En cambio, no sería una variable el planeta donde se han producido las elecciones, porque todas se han producido en la Tierra. La gravedad también sería la misma y en cada observación también hay la misma presencia de oxígeno, por lo que estas dos características, si estuvieran en este conjunto de datos, no las podríamos considerar variables.
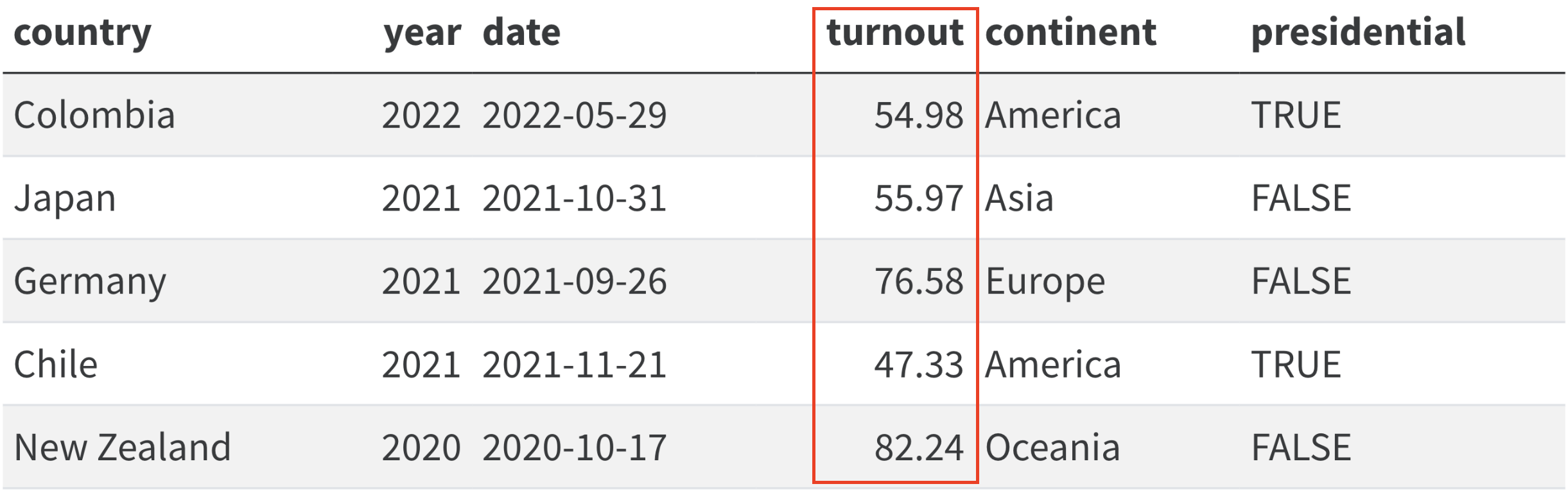
Como podemos ver, las variables suelen estar formadas por números (como los valores de turnout o de year), o bien por categorías (como los valores de country o de continent). Pero, al margen de esta primera distinción, lo importante es distinguirlas por las operaciones que permiten realizar con sus valores. En la tabla 11.1, observamos los cuatro tipos principales de variables. Con las variables nominales, solo podemos saber si sus valores son iguales o diferentes. En cambio, con las variables ordinales también podemos ordenar sus valores. A diferencia de las ordinales, las variables de intervalo tienen valores con significado, por lo que en algunas ocasiones podremos realizar operaciones como sumas y restas. Y, finalmente, con las variables de ratio podremos hacer todo tipo de operaciones, como sumar, restar, multiplicar o dividir.
| Tipos | Características | Vector | Operaciones |
|---|---|---|---|
| Categórica nominal | Categorías no ordenables | Carácter o factor |
==, !=
|
| Categórica ordinal | Categorías ordenables | Factor |
==, !=, <=, <, >, >=
|
| Numérica de intervalo | Números, cero sin significado | Numérico o entero |
==, !=, <=, <, >, >=, +, -
|
| Numérica de ratio | Números, cero con significado | Numérico |
==, !=, <=, <, >, >=, +, -, *, / … |
Hasta ahora hemos estudiado la columna, la variable y el vector como tres conceptos que parecen idénticos. Pero ¿son lo mismo? La respuesta es no, aunque es fácil confundirlos porque a menudo sirven para el mismo propósito. Para distinguirlos, diremos que:
- La columna se refiere a la distribución vertical de los valores en una tabla.
- La variable es un constructo abstracto, una propiedad del fenómeno que estamos estudiando que varía entre observaciones.
- El vector es una herramienta de R que nos permite almacenar datos en forma de concatenado.
A pesar de estas diferencias, es cierto que muchas veces la columna, la variable y el vector se solapan. Para analizar fenómenos, en R solemos guardar las variables en forma de vectores. Y cada vector forma una columna de un marco de datos. Más adelante veremos, sin embargo, que no siempre coincide (véase por ejemplo, el marco de datos tidyr::world_bank_pop, en el que las variables son valores de la columna indicator y los años son nombres de variables en lugar de valores).
11.2 Variables nominales
Las variables categóricas nominales (también podemos llamarlas simplemente variables nominales) agrupan sus valores en categorías diferentes, asumiendo que no siguen ningún orden concreto. Lo único que podemos hacer es clasificarlas. Podemos, por ejemplo, clasificar por su nombre los estados que existen en el mundo, los colores, las religiones, la nacionalidad de una persona, el lugar de nacimiento o el sexo. Pero no podemos ni ordenar ni cuantificar estas características numéricamente: no tiene sentido decir que el nombre «amarillo» es superior a «morado» o multiplicar «Brasil» por «Honduras». Lo único que podemos hacer es decir si un valor de la variable es igual o diferente a otro.
En R, almacenaremos las variables nominales como vectores de carácter o como factores. En esencia, no hay ninguna diferencia al guardar una variable nominal en un vector de carácter o en un factor.
11.2.1 Operaciones con variables nominales
Para realizar algunas operaciones con variables nominales, hemos creado el marco de datos strings a partir de una adaptación de los datos del paquete countrycode (Arel-Bundock, 2022). En el argot de R, la palabra string se utiliza para denominar los vectores de carácter:
strings <- tribble(~iso3c, ~country, ~currency, ~continent, ~region,
"CMR", "Cameroon", "CFA Franc BEAC", "Africa", "Sub-Saharan Africa",
"COL", "Colombia", "Colombian Peso", "Americas", "Latin America & Caribbean",
"CUB", "Cuba", "Cuban Peso", "Americas", "Latin America & Caribbean",
"FRA", "France", "Euro", "Europe", "Europe & Central Asia",
"LSO", "Lesotho", "Loti", "Africa", "Sub-Saharan Africa",
"QAT", "Qatar", "Qatari Rial", "Asia", "Middle East & North Africa",
"TWN", "Taiwan", "New Taiwan Dollar", "Asia", "East Asia & Pacific",
"TTO", "Trinidad & Tobago", "Trinidad & Tobago Dollar", "Americas", "Latin America & Caribbean")
strings
## # A tibble: 8 × 5
## iso3c country currency continent region
## <chr> <chr> <chr> <chr> <chr>
## 1 CMR Cameroon CFA Franc BEAC Africa Sub-Saharan Africa
## 2 COL Colombia Colombian Peso Americas Latin America & Ca…
## 3 CUB Cuba Cuban Peso Americas Latin America & Ca…
## 4 FRA France Euro Europe Europe & Central A…
## 5 LSO Lesotho Loti Africa Sub-Saharan Africa
## 6 QAT Qatar Qatari Rial Asia Middle East & Nort…
## 7 TWN Taiwan New Taiwan Dollar Asia East Asia & Pacific
## 8 TTO Trinidad & Tobago Trinidad & Tobago Dollar Americas Latin America & Ca…Con las operaciones que vemos en el recuadro de la derecha, podemos responder preguntas como las siguientes:
Al tener pocas propiedades matemáticas, con las variables nominales solo podemos realizar operaciones de:
- Igualdad (
==,%in%) - No igualdad (
!=)
%in%
Con operaciones con más de un valor categórico, utilizaremos %in%. Por ejemplo, si del vector var queremos que nos devuelva v1, v2 y v3, utilizaremos el código siguiente:
var %in% c("v1","v2","v3") ¿Qué observación es Cameroon? Del marco de datos strings, seleccionamos las observaciones en las que la variable country sea igual a "Cameroon".
strings[strings$country == "Cameroon",]
## # A tibble: 1 × 5
## iso3c country currency continent region
## <chr> <chr> <chr> <chr> <chr>
## 1 CMR Cameroon CFA Franc BEAC Africa Sub-Saharan Africa¿Qué países están en África o en Europa? Del marco de datos strings, seleccionamos las observaciones en las que la variable continent sea igual a "Africa" o "Europe".
strings[strings$continent %in% c("Africa", "Europe"),]
## # A tibble: 3 × 5
## iso3c country currency continent region
## <chr> <chr> <chr> <chr> <chr>
## 1 CMR Cameroon CFA Franc BEAC Africa Sub-Saharan Africa
## 2 FRA France Euro Europe Europe & Central Asia
## 3 LSO Lesotho Loti Africa Sub-Saharan Africa¿Qué países no están en la región de América Latina y el Caribe? Del marco de datos strings, seleccionamos las observaciones en las que la variable region sea no igual a "Latin America & Caribbean".
strings[strings$region != "Latin America & Caribbean",]
## # A tibble: 5 × 5
## iso3c country currency continent region
## <chr> <chr> <chr> <chr> <chr>
## 1 CMR Cameroon CFA Franc BEAC Africa Sub-Saharan Africa
## 2 FRA France Euro Europe Europe & Central Asia
## 3 LSO Lesotho Loti Africa Sub-Saharan Africa
## 4 QAT Qatar Qatari Rial Asia Middle East & North Africa
## 5 TWN Taiwan New Taiwan Dollar Asia East Asia & PacificMás adelante, veremos como con otras variables podremos realizar operaciones más complejas. Puesto que las categorías de las variables nominales no son ordenables, no permiten saber si una categoría es mayor que otra o sumar y restar categorías. Sin embargo, debemos saber que los vectores de carácter y los factores tienen asociada una ordenabilidad alfabética1.
1 Los vectores de carácter, y también los factores, están ordenados alfabéticamente, donde «A» es el valor más pequeño y «Z» el valor más grande. Esta ordenación nos puede convenir puntualmente, pero no debemos concebir las variables nominales como ordenables.
11.2.2 Otros ejemplos de variables nominales
En la base de datos siguiente vemos un fragmento de la Global Terrorism Database (START, 2022), que tiene recontados más de 200.000 ataques terroristas desde 1970 hasta la actualidad, incluyendo bombardeos, asesinatos y secuestros. Como podemos ver en la tabla 11.2, las variables country_txt, provstate, city, attacktype1_txt, targtype1_txt y weapdetail son nominales2.
2 Podríamos presuponer cierta ordinalidad en attacktype1_txt y weapdetail.
| iyear | country_txt | provstate | city | latitude | longitude | attacktype1 | attacktype1_txt | targtype1 | targtype1_txt | weapdetail |
|---|---|---|---|---|---|---|---|---|---|---|
| 1970 | Dominican Republic | National | Santo Domingo | 18.45679 | -69.95116 | 1 | Assassination | 14 | Private Citizens & Property | NA |
| 1970 | Mexico | Federal | Mexico city | 19.37189 | -99.08662 | 6 | Hostage Taking (Kidnapping) | 7 | Government (Diplomatic) | NA |
| 1970 | Philippines | Tarlac | Unknown | 15.47860 | 120.59974 | 1 | Assassination | 10 | Journalists & Media | NA |
| 1970 | Greece | Attica | Athens | 37.99749 | 23.76273 | 3 | Bombing/Explosion | 7 | Government (Diplomatic) | Explosive |
| 1970 | Japan | Fukouka | Fukouka | 33.58041 | 130.39636 | 7 | Facility/Infrastructure Attack | 7 | Government (Diplomatic) | Incendiary |
| 1970 | United States | Illinois | Cairo | 37.00511 | -89.17627 | 2 | Armed Assault | 3 | Police | Several gunshots were fired. |
| 1970 | Uruguay | Montevideo | Montevideo | -34.89115 | -56.18721 | 1 | Assassination | 3 | Police | Automatic firearm |
| 1970 | United States | California | Oakland | 37.79193 | -122.22591 | 3 | Bombing/Explosion | 21 | Utilities | NA |
También hemos visto anteriormente en bases de datos de este capítulo ejemplos de variables nominales:
- El nombre del país (
ctryname) en la tabla 10.5. - El nombre del líder político (
leader) en la tabla 10.8. - El nombre del grupo étnico (
group) en la tabla 10.6.
Otras variables nominales pueden ser el municipio (Barcelona, Sant Cugat, Granollers…), la religión (musulmana, católica, sintoísta…), la lengua (ruso, catalán, sueco…), la ideología (conservadora, progresista, liberal…), la organización internacional (Unión Europea, Mercosur, ASEAN…) o el tipo de mercancía (transporte, maquinaria, textil…).
11.2.3 Variables binarias
Las variables binarias (también denominadas dicotómicas o dummy) son conceptualmente un subtipo de variable categórica nominal en la que la característica del objeto que estamos estudiando solo puede adoptar dos valores: ausencia o presencia (Goertz, 2020, págs. 137-138). Operativamente, sin embargo, podemos tratar estas variables como vector de carácter, como factor, como vector numérico e incluso como vector lógico. No hay ninguna norma clara de cómo guardarlas inicialmente. Lo más normal es que más adelante las transformemos de un tipo de vector a otro en función de nuestro propósito3.
3 Por ejemplo, si queremos visualizar datos, las transformaremos en vectores de carácter o factores, mientras que, si queremos realizar un análisis bivariante, las transformaremos en vectores numéricos. Pasarlas a vector lógico es factible, pero poco habitual.
Cuando importamos datos a R, lo más frecuente será encontrar las variables binarias codificadas en un vector numérico con 1 y 0. El valor 1 indicará la presencia del concepto y el 0 la ausencia. En la siguiente tabla 11.3, observamos un fragmento de la Formal Alliances dataset (Gibler, 2009; Singer & Small, 1966), formada principalmente por variables binarias. Cada unidad de observación es la alianza entre dos países. Entre sus características, se encuentra el año de creación (dyad_st_year), el año de finalización (dyad_end_year), si es una alianza de defensa (defense), de neutralidad (neutrality), un pacto de no agresión (nonaggression) o una entente (entente).
| version4id | state_name1 | state_name2 | dyad_st_year | dyad_end_year | defense | neutrality | nonaggression | entente |
|---|---|---|---|---|---|---|---|---|
| 1 | United Kingdom | Portugal | 1816 | NA | 1 | 0 | 1 | 0 |
| 2 | United Kingdom | Sweden | 1816 | 1911 | 0 | 0 | 0 | 1 |
| 3 | Hanover | Bavaria | 1838 | 1848 | 1 | 0 | 1 | 1 |
| 3 | Hanover | Bavaria | 1850 | 1866 | 1 | 0 | 1 | 1 |
| 3 | Hanover | Germany | 1850 | 1866 | 1 | 0 | 1 | 1 |
| 3 | Hanover | Germany | 1838 | 1848 | 1 | 0 | 1 | 1 |
| 3 | Hanover | Baden | 1838 | 1848 | 1 | 0 | 1 | 1 |
| 3 | Hanover | Baden | 1850 | 1866 | 1 | 0 | 1 | 1 |
Cuando encontramos una variable binaria en un marco de datos, lo más recomendable es dejarla como está. Normalmente, esto significará dejarla como vector numérico y, en todo caso, ya recodificaremos la variable más adelante si lo necesitamos. En el supuesto de que quisiéramos transformar la variable a categórica, recomendamos almacenarla en forma de factor. Si suponemos que el marco de datos tiene como nombre ally, utilizaríamos el procedimiento siguiente para convertir la variable defense en factor4.
4 Lo mismo podríamos hacer con neutrality, nonaggression y entente.
En este capítulo hemos visto varios casos de variables binarias. Por ejemplo:
- Si el líder político fue o no elegido (
elected) en la tabla 10.8. - Si un golpe de estado fue exitoso o no (
successful) en la tabla 10.7. - Si el grupo étnico tiene autonomía regional o no (
reg_aut) en la tabla 10.6.
Lo que es importante es que el nombre del vector numérico permita identificar claramente qué sentido toma la variable en caso de presencia. El vector male no tendría sentido ponerlo como sex si está codificado con 1 y 0, porque no sabríamos qué sexo es 1 y qué sexo es 0. En cambio, si la recodificásemos como factor, sí tendría más sentido poner sex y que tuviera como posibles valores «Male» y «Female» o bien «Other».
11.2.4 El paquete stringr
Para manipular los vectores de carácter, la mejor herramienta que podemos utilizar es el paquete stringr (Wickham, 2023b). En este apartado no explicaremos todas las funciones del paquete. Lo más adecuado es consultar su Cheatsheet correspondiente en la página de RStudio. Pero a continuación veremos algunas funciones con el mismo marco de datos strings que hemos creado anteriormente:
Con str_remove() podemos eliminar una serie de caracteres de los valores de una variable. A continuación, eliminamos "Latin " (prestad atención al espacio) de la variable region.
str_remove(strings$region, "Latin ")
## [1] "Sub-Saharan Africa" "America & Caribbean"
## [3] "America & Caribbean" "Europe & Central Asia"
## [5] "Sub-Saharan Africa" "Middle East & North Africa"
## [7] "East Asia & Pacific" "America & Caribbean"Con str_replace() podemos sustituir unos caracteres por otros. A continuación, sustituimos «&» de la variable country por «and».
str_replace(strings$country, "&", "and")
## [1] "Cameroon" "Colombia" "Cuba"
## [4] "France" "Lesotho" "Qatar"
## [7] "Taiwan" "Trinidad and Tobago"Con str_to_upper() ponemos todos los caracteres en mayúsculas. A continuación, ponemos el nombre de la moneda de la variable currency en mayúsculas.
str_to_upper(strings$currency)
## [1] "CFA FRANC BEAC" "COLOMBIAN PESO"
## [3] "CUBAN PESO" "EURO"
## [5] "LOTI" "QATARI RIAL"
## [7] "NEW TAIWAN DOLLAR" "TRINIDAD & TOBAGO DOLLAR"De una forma muy parecida, str_to_sentence() pone la primera letra de la frase en mayúsculas, str_to_lower() todas las letras en minúsculas, str_to_title() la primera letra de cada palabra en mayúsculas.
Con str_sub() quitamos el último carácter de la variable iso3c, de forma que nos queda un código de país de dos caracteres.
str_sub(strings$iso3c, end = 2)
## [1] "CM" "CO" "CU" "FR" "LS" "QA" "TW" "TT"11.3 Variables ordinales
Las variables categóricas ordinales (o, simplemente, variables ordinales) agrupan las observaciones en categorías diferentes que siguen un orden lógico concreto. Por ejemplo, podemos ordenar las personas en función de si son «niños», «jóvenes» o «adultos», o bien su nivel educativo en «sin estudios», «estudios primarios», «estudios secundarios» o «estudios superiores». Así, podemos saber si una categoría es superior o inferior a otra. Lo que no podemos saber con esta variable es la distancia que hay entre categorías. No sabemos, por ejemplo, si hay la misma distancia entre «sin estudios» y «estudios primarios» que entre «estudios primarios» y «estudios secundarios», simplemente por el hecho de que no hay ningún intervalo numérico asociado a cada variable. Lo único que podemos hacer es comparar las categorías entre ellas en términos de ser más, menos, igual que o diferente a otra.
En R, almacenaremos las variables ordinales como factores ordenables.
11.3.1 Operaciones con variables ordinales
Para realizar algunas operaciones con variables ordinales hemos creado el marco de datos ords, que contiene una clasificación de agencias donantes de ayuda al desarrollo y su puntuación ordinal en el ranking Aid Transparency Index (ATI) de 2022 que publica para la ONG Publish What You Fund. Esta clasificación ordinal establece hasta qué punto la agencia donante publica de forma transparente qué se gasta, quién lo gasta y dónde se gasta. El marco de datos también incluye a qué tipo de régimen pertenece la agencia donante según la clasificación ordinal de democracia del Economist Intelligence Unit de 2022.
ords <- tibble(donor = c("US-MCC", "Canada-GAC", "Germany-BMZ-GIZ", "Korea-KOICA", "Australia-DFAT", "Spain-AECID",
"Saudi Arabia-KSRelief", "Norway-MFA", "China-MOFCOM", "Turkey-TIKA"),
ati = factor(c("Very Good", "Good", "Good", "Good", "Good", "Fair",
"Poor", "Poor", "Very Poor", "Very Poor"),
ordered = TRUE,
levels = c("Very Poor", "Poor", "Fair", "Good", "Very Good")),
regime_type = factor(c("Flawed Democracy", "Full Democracy", "Full Democracy", "Full Democracy", "Full Democracy",
"Flawed Democracy", "Authoritarian", "Full Democracy", "Authoritarian", "Hybrid Regime"),
ordered = TRUE,
levels = c("Authoritarian", "Hybrid Regime", "Flawed Democracy", "Full Democracy")))
ords
## # A tibble: 10 × 3
## donor ati regime_type
## <chr> <ord> <ord>
## 1 US-MCC Very Good Flawed Democracy
## 2 Canada-GAC Good Full Democracy
## 3 Germany-BMZ-GIZ Good Full Democracy
## 4 Korea-KOICA Good Full Democracy
## 5 Australia-DFAT Good Full Democracy
## 6 Spain-AECID Fair Flawed Democracy
## 7 Saudi Arabia-KSRelief Poor Authoritarian
## 8 Norway-MFA Poor Full Democracy
## 9 China-MOFCOM Very Poor Authoritarian
## 10 Turkey-TIKA Very Poor Hybrid RegimeCon las operaciones que vemos en el recuadro de la derecha, podemos responder preguntas como las siguientes:
Con las variables ordinales podemos hacer operaciones de:
- Igualdad (
==,%in%) - No igualdad (
!=) - Mayor que (
>) - Mayor o igual que (
>=) - Menor que (
<) - Menor o igual que (
<=)
¿Qué agencias pertenecen a democracias débiles? Del marco de datos ords, seleccionamos las observaciones en las que la variable regime_type sea igual a "Flawed Democracy".
ords[ords$regime_type == "Flawed Democracy",]
## # A tibble: 2 × 3
## donor ati regime_type
## <chr> <ord> <ord>
## 1 US-MCC Very Good Flawed Democracy
## 2 Spain-AECID Fair Flawed Democracy¿Qué agencias tienen un ATI como mínimo bueno? Del marco de datos ords, seleccionamos las observaciones en las que la variable ati sea mayor o igual que "Good".
ords[ords$ati >= "Good",]
## # A tibble: 5 × 3
## donor ati regime_type
## <chr> <ord> <ord>
## 1 US-MCC Very Good Flawed Democracy
## 2 Canada-GAC Good Full Democracy
## 3 Germany-BMZ-GIZ Good Full Democracy
## 4 Korea-KOICA Good Full Democracy
## 5 Australia-DFAT Good Full Democracy¿Qué agencias tienen un ATI inferior a correcto? Del marco de datos ords, seleccionamos las observaciones en las que la variable ati sea menor que "Fair".
ords[ords$ati < "Fair",]
## # A tibble: 4 × 3
## donor ati regime_type
## <chr> <ord> <ord>
## 1 Saudi Arabia-KSRelief Poor Authoritarian
## 2 Norway-MFA Poor Full Democracy
## 3 China-MOFCOM Very Poor Authoritarian
## 4 Turkey-TIKA Very Poor Hybrid RegimeAparte de las operaciones de igualdad, las variables ordinales permiten saber si una categoría es mayor o menor que otra. Sin embargo, como no conocemos la distancia entre categorías, por ejemplo, entre «Fair» y «Poor», no podemos realizar operaciones más complejas como sumar y restar. Estas operaciones las podremos realizar con las variables numéricas.
11.3.2 Importar datos ordinales
Cuando importamos bases de datos a R, raramente nos encontraremos las variables ordinales codificadas como factor ordinal. Normalmente, nos encontraremos con una de las situaciones siguientes:
| code | income_group |
|---|---|
| AFG | Low income |
| ALB | Upper middle income |
| DZA | Upper middle income |
| ASM | Upper middle income |
| AND | High income |
| AGO | Lower middle income |
| ATG | High income |
| ARG | Upper middle income |
Las variables ordinales están codificadas como vector de carácter (1). Este es el caso, por ejemplo, de la variable
income_group, una clasificación producida por el Banco Mundial que ordena grupos de países según niveles de renta per cápita. Observamos un fragmento de estos datos en la tabla 11.4 del lateral.Las variables ordinales nos llegan codificadas como vector numérico (2). Este es el caso de muchos datos de encuesta, en los que las respuestas que llevan asociadas categorías como «Mucho», «Bastante», «Poco» o «Nada» suelen estar codificadas numéricamente (tabla 11.5).
En ambos casos, las variables tendrán que ser recodificadas en factor ordinal con un procedimiento muy parecido. Por ahora, debemos saber que para hacer la conversión utilizaremos la función factor() y dentro introduciremos tres argumentos: el vector, la indicación de que es ordinal en el vector ordrered y, en un tercer argumento, los niveles (levels) o bien los hashtags (labels) del factor.
| CCOW | YEAR | Q1 | Q2 | Q3 | Q4 |
|---|---|---|---|---|---|
| AND | 2018 | 1 | 1 | 1 | 3 |
| AND | 2018 | 1 | 1 | 1 | 4 |
| AND | 2018 | 1 | 2 | 2 | 2 |
| AND | 2018 | 1 | 1 | 1 | 4 |
| AND | 2018 | 1 | 1 | 1 | 3 |
| AND | 2018 | 1 | 3 | 1 | 4 |
factor(vector,
ordered = TRUE,
levels = c("Bajo", "Medio", "Alto"))En el apartado Recodificaciones de variables trataremos estos dos casos en detalle y veremos también la diferencia entre levels y labels.
En este vídeo encontramos un resumen de los operadores relacionales que hemos visto:
11.3.3 El paquete forcats
Para manipular los factores, la mejor herramienta que podemos utilizar es el paquete forcats (Wickham, 2023a). En este apartado solo veremos algunas de sus funciones, pero para explorarlo más a fondo podéis consultar su Cheatsheet correspondiente en la página de RStudio. A continuación, aplicaremos algunas funciones al marco de datos ords que hemos creado anteriormente. La mayoría de estas funciones van relacionadas con reordenar factores y son muy útiles para visualizar gráficos.
Con fct_relevel() cambiamos rápidamente el orden de los niveles. En el primer argumento indicamos el factor y en el resto de los argumentos indicamos, en orden ascendente, los niveles.
fct_relevel(ords$regime_type, "Hybrid Regime", "Full Democracy", "Flawed Democracy", "Authoritarian")
## [1] Flawed Democracy Full Democracy Full Democracy Full Democracy
## [5] Full Democracy Flawed Democracy Authoritarian Full Democracy
## [9] Authoritarian Hybrid Regime
## 4 Levels: Hybrid Regime < Full Democracy < ... < AuthoritarianCon fct_rev() cambiamos el orden de los niveles.
fct_rev(ords$ati)
## [1] Very Good Good Good Good Good Fair Poor
## [8] Poor Very Poor Very Poor
## Levels: Very Good < Good < Fair < Poor < Very PoorCon fct_other() creamos un nivel formado por varias categorías. En el primer argumento indicamos el factor y en el segundo indicamos las categorías que queremos conservar.
fct_other(ords$ati, keep = c("Good", "Very Good"))
## [1] Very Good Good Good Good Good Other Other
## [8] Other Other Other
## Levels: Good < Very Good < OtherCon fct_infreq() ordenamos los niveles en función de su número de frecuencias en la base de datos (es decir, en función de las veces que aparecen). Esta función es muy útil cuando la combinamos con funciones que reproducen gráficos.
plot(fct_infreq(ords$ati))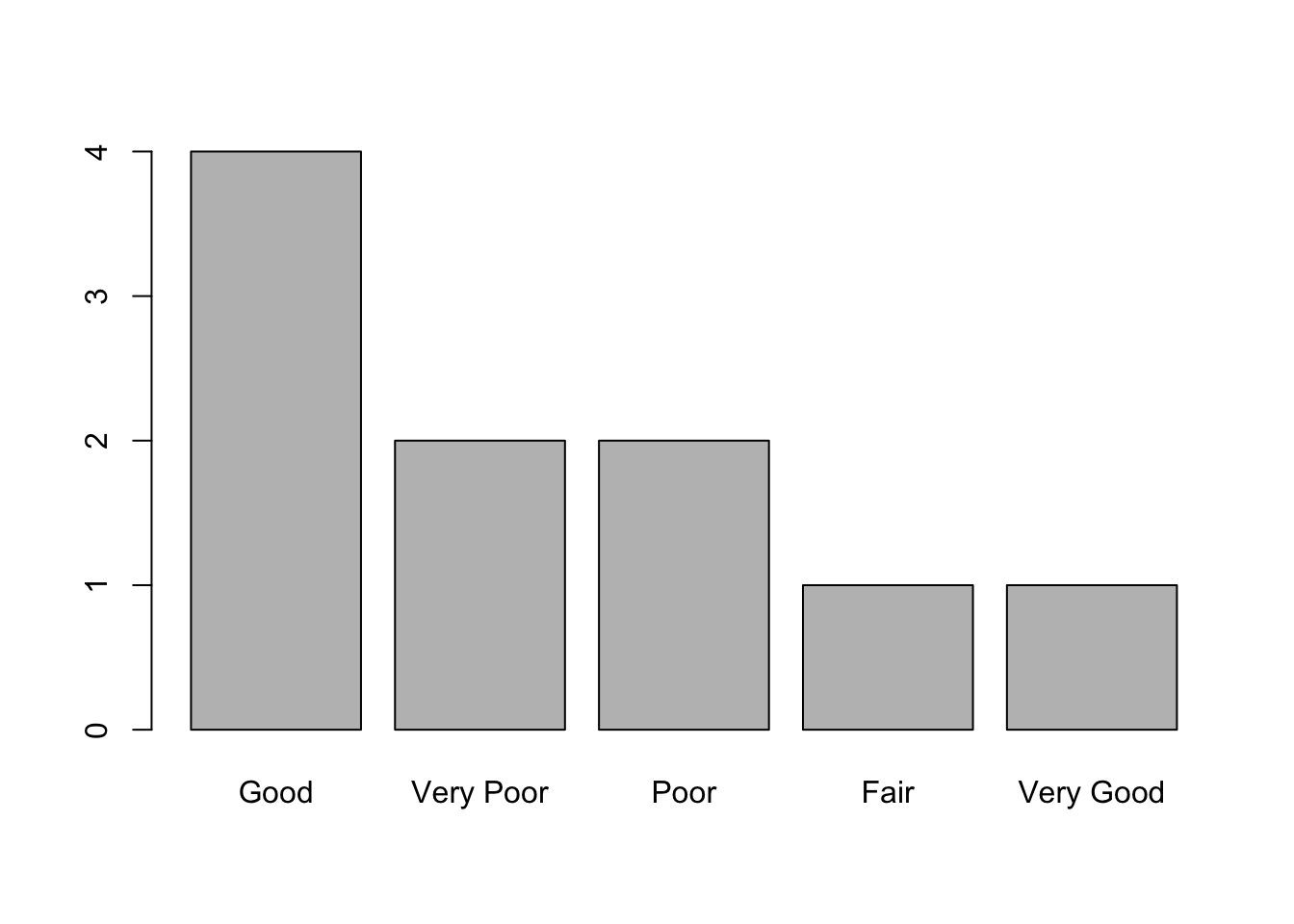
Si combinamos fct_infreq() y fct_rev(), obtendremos los niveles en el orden contrario.
plot(fct_rev(fct_infreq(ords$ati)))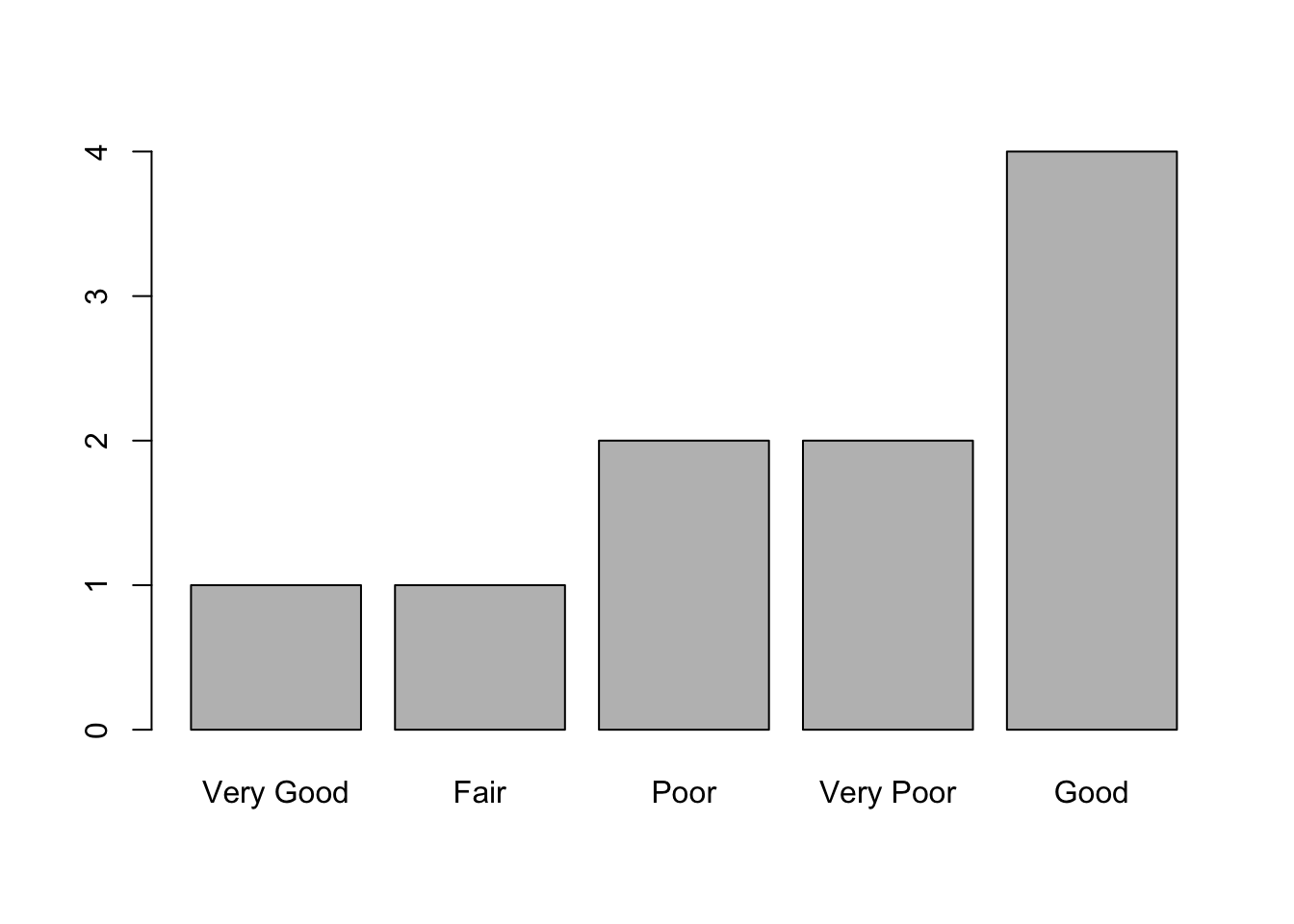
Todas las funciones de forcats son útiles para factores, tanto para representar variables nominales como para representar variables ordinales.
11.4 Variables de intervalo
A diferencia de las variables categóricas, las variables numéricas agrupan las observaciones en números. Las variables numéricas de intervalo (o simplemente variables de intervalo) tienen como principal propiedad que la distancia entre sus valores tiene significado, pero que el valor cero no indica la ausencia del valor en concreto. Así, con las variables de intervalo podemos hacer las mismas operaciones que con las variables ordinales (saber si un valor es mayor o menor que otro) y, además, también podemos saber cuán grande o pequeño es este valor porque la distancia numérica es conocida.
Un ejemplo es la variable año, cuando nos referimos a los años de calendario5. Pongamos por caso que tenemos tres valores de intervalo: 1919, 1945 y 1989. Podemos saber si un año es menor o mayor que otro, pero también podemos saber qué distancia hay entre estos valores. Por ejemplo, sabemos que hay una diferencia de veintiséis años entre 1919 y 1945 y una diferencia de setenta años entre 1919 y 1989. Esta es una operación que no podríamos realizar con variables ordinales.
5 A diferencia de la variable año cuando nos referimos a los años de una persona o los años de duración de un determinado fenómeno. En este caso, el cero sí que tiene significado.
Con las variables de intervalo, sin embargo, no podremos calcular la ratio entre sus valores, puesto que una de las propiedades que le falta a este tipo de variables es que el valor cero no significa «ausencia de». En el ejemplo de los años del calendario, el año cero no significa ausencia de nada en concreto, como la ausencia de años o ausencia de tiempo. Lo entenderemos mejor con otro ejemplo: la temperatura en grados Celsius6: los cero grados no representan la ausencia de calor ni la ausencia de temperatura. Por lo tanto, cuando la temperatura sube de 10 a 20 grados, no podremos decir que el calor se ha duplicado.
6 El ejemplo también vale para grados Fahrenheit. En cambio, la temperatura en grados Kelvin sí que es una variable de ratio, puesto que el cero indica la ausencia de calor y, por lo tanto, pasar de 100 a 200 grados Kelvin querría decir que se duplica el calor.
En R, las variables de intervalo se almacenan preferiblemente como vectores numéricos, aunque en algunos casos las podremos almacenar como vectores enteros o vectores de fecha.
11.4.1 Operaciones con variables de intervalo
Para hacer algunas operaciones con variables de intervalo hemos creado el marco de datos polity, que muestra el nivel de democracia que tenían varios países en su año de fundación según la base de datos Polity V (Marshall & Gurr, 2020). Esta base de datos asigna un nivel de democracia a los regímenes políticos entre -10 y 10, donde 10 es el nivel máximo de democracia. El cero, en este caso, no significa «ausencia de», sino que es un nivel intermedio que adopta un régimen político en esta escala7.
7 Y aunque la escala estuviera construida de 0 a 10, el cero tampoco significa «ausencia de» democracia.
polity <- tibble(country = c("United States", "Bolivia", "Australia", "Azerbaijan",
"USSR", "Timor Leste", "Eritrea", "Qatar", "Gambia"),
year = c(1776, 1825, 1901, 1991, 1922, 2002, 1993, 1971, 1965),
polity2 = c(0, -3, 10, -3, -7, 6, -6, -10, 8))
polity
## # A tibble: 9 × 3
## country year polity2
## <chr> <dbl> <dbl>
## 1 United States 1776 0
## 2 Bolivia 1825 -3
## 3 Australia 1901 10
## 4 Azerbaijan 1991 -3
## 5 USSR 1922 -7
## 6 Timor Leste 2002 6
## 7 Eritrea 1993 -6
## 8 Qatar 1971 -10
## 9 Gambia 1965 8Con las operaciones que vemos en el recuadro, podemos responder preguntas como las siguientes:
¿Cuántos años de diferencia hay entre la fundación de los Estados Unidos y la fundación de la Unión Soviética?
polity$year[polity$country == "United States"] - polity$year[polity$country == "USSR"]
## [1] -146En sus respectivos años de fundación, ¿el nivel de democracia de Bolivia era mayor que el de Eritrea?
polity$polity2[polity$country == "Bolivia"] > polity$polity2[polity$country == "Eritrea"]
## [1] TRUE¿Qué regímenes políticos tenían niveles de democracia superiores en los Estados Unidos en su año de fundación?
polity$country[polity$polity2[polity$country == "United States"] > polity$polity2]
## [1] "Bolivia" "Azerbaijan" "USSR" "Eritrea" "Qatar"11.4.2 Importar datos de intervalo
En la mayoría de los casos, las variables de intervalo se importan a R como vectores numéricos. Está bien que se importen así y no tendremos que hacer ninguna transformación adicional. En algunos casos, es fácil confundir las variables de intervalo con otros tipos de variables, como las ordinales o las de ratio.
También hemos visto anteriormente ejemplos de bases de datos con variables de intervalo:
- Todas las variables que contienen la variable año, como
yearen las tablas tabla 10.5, tabla 10.4 y tabla 10.7. - Variables que muestran una fecha concreta (
date) en la tabla 10.7. - La latitud (
latitude) y la longitud (longitude) de la tabla 11.2.
El eje izquierda-derecha es una de las variables más empleadas en Ciencia Política. En la tabla 11.6, que es un fragmento de la Global Party Survey, la vemos en V4_Scale (Norris, 2020). En las encuestas, se suele preguntar: «Ubíquese ideológicamente, donde 0 es extrema izquierda y 10 extrema derecha». ¿Es esta una variable de intervalo? Obviamente, el cero no tiene significado, porque no significa ausencia de ideología, por lo cual podemos descartar que sea una variable de ratio. Fijémonos en que podríamos construir una escala donde, por ejemplo, el cero indicara el centro, -10 la izquierda y +10 la derecha. O bien que fuera 90 derecha y 100 izquierda. Como vemos, una de las propiedades de la escala de intervalo es que podemos ubicar el principio y el final de la escala en cualquier lugar. Y esto es así porque el cero no tiene ningún significado y los valores de las escalas son completamente móviles y arbitrarios.
Lo que resulta más difícil de decir es si la autoubicación ideológica es una variable de intervalo u ordinal. La principal diferencia entre las dos es que en las variables ordinales hay una distancia conocida e igual entre los niveles de la escala. Pasar de 4 a 5 en el eje ideológico tendría que significar lo mismo que pasar de 5 a 6. Y esto es cuestionable. Por este motivo, algunos autores (ver Johnson et al., 2016, pág. 351) defienden que la ideología es técnicamente una construcción ordinal, aunque en la práctica las escalas ordinales construidas con números se puedan acabar considerando variables de intervalo. Una regla no escrita es que, si una variable ordinal está formada por siete o más valores, se puede considerar de intervalo (Goertz, 2020, págs. 139, 144).
| Partyname | Partyabb | V4_Scale | V4_Ord |
|---|---|---|---|
| Brexit Party | BRX | 8.653846 | Strongly economically-right |
| Conservative and Unionist Party | CON | 7.916667 | Strongly economically-right |
| Democratic Unionist Party | DUP | 7.000000 | Center economically-right |
| Green Party | GRN | 2.526316 | Center economically-left |
| Labour Party | Lab | 2.125000 | Strongly economically-left |
| Liberal Democrats | LD | 4.666667 | Center economically-left |
| Plaid Cymru | PC | 3.235294 | Center economically-left |
| Scottish National Party | SNP | 3.162162 | Center economically-left |
| Sinn Féin | SF | 2.708333 | Center economically-left |
| UK Independence Party | UKIP | 8.086956 | Strongly economically-right |
11.4.3 El paquete lubridate
Una de las principales variables de intervalo es la de las fechas de calendario. Con esto nos podemos referir tanto a variables como el año (2013, 2014, 2015…) como a variables más concretas que tengan como valores fechas exactas (por ejemplo, «1952-03-10», como hemos visto en la variable date de la tabla 10.7) o todavía más concretas, como sería «1961-01-20 13:00:00». Cuando solo necesitamos el año como variable, tendremos suficiente con almacenarlo como vector numérico, sin necesidad de hacer ninguna transformación especial. Pero, a medida que el tiempo sea un factor importante de nuestro estudio y necesitemos jugar con meses, semanas, días u horas, más importante será utilizar el paquete lubridate (Spinu et al., 2023).
No entraremos a explicarlo en detalle en este módulo, porque es un paquete que se utiliza para necesidades muy concretas. Sin embargo, debemos saber que nos permite realizar operaciones como distinguir qué fechas caen en fin de semana, crear niveles ordinales entre días de la semana, calcular diferencias entre fechas o calcular diferencias entre franjas horarias.
11.5 Variables de ratio
A diferencia de las otras variables que hemos visto, las variables numéricas de ratio (o simplemente, variables de ratio) tienen todas las propiedades matemáticas. Podemos decir si los números son iguales o diferentes, si son mayores o menores, qué distancia hay entre ellos y también podemos saber la cantidad relativa de cada valor. La propiedad distintiva de las variables de ratio es que el cero tiene significado. Esto quiere decir que hay un punto de referencia que marca la ausencia del fenómeno. El cero en la edad de una persona significa ausencia de años, así como el cero en la tasa de paro significa la ausencia de paro y el cero en población significa que aquel país o territorio no tiene población.
Cuando tratemos con variables numéricas, a menudo veremos los valores representados con notación científica:
12000000
## [1] 1.2e+07Interpretarlos es más fácil de lo que parece, puesto que simplemente tenemos que mover los decimales tantas veces a la derecha como nos indique el último número si es positivo, o tantas veces a la izquierda si es negativo. Por ejemplo, 2.50+e08 se traducirá como 250.000.000.
Dado que el cero tiene significado, podemos utilizarlo para establecer relaciones entre los valores de la variable por medio de operaciones matemáticas más complejas, como multiplicar, dividir, hacer raíces cuadradas, etc. Por ejemplo, podemos decir que diez años son el doble que cinco o que, si el paro varía del 10 % al 5 %, se ha reducido a la mitad. Estas son operaciones que no podemos realizar con los otros tipos de variables que hemos visto. Por ejemplo, con la escala de intervalo de Polity V no podemos decir que un país es el doble de democrático que otro. Ni tampoco podemos decir que un país categorizado como «Low Income» sea la mitad que «Lower Middle Income». Esto es debido a que el cero, que es un punto real de referencia en las variables de ratio, no existe ni tiene significado propio en las otras variables. Por lo tanto, desde un punto de vista del análisis cuantitativo, las variables de ratio son preferibles a los demás tipos de variables porque permiten realizar más operaciones matemáticas.
En R, almacenaremos las variables de ratio como vectores numéricos. Algunas de ellas también las podríamos almacenar como vectores enteros.
11.5.1 Operaciones con variables de ratio
Para realizar algunas operaciones con variables de ratio, hemos recreado las capacidades materiales de las principales potencias participantes en la Segunda Guerra Mundial en 1939 a partir de los datos de la National Material Capabilities (NMC) dataset (Singer et al., 1972; Singer, 1987). El marco de datos ratios contiene la variable gasto militar (milex, en miles de dólares), personal militar (milper, en miles), total de población (tpop, en miles) y el índice CINC (cinc)8, que es una medida compuesta que calcula las capacidades materiales relativas de un país en un año determinado.
8 Responde al acrónimo Composite Index of National Capability. La variable milex responde al gasto militar, milper a personal militar y tpop a población total. Estas y otras variables forman el índice cinc.
ratio <- tibble(country = c("USA", "UKG", "FRN", "GMY", "ITA", "RUS", "JPN"),
milex = c(980000, 7895671, 1023651, 12000000, 669412, 5984123, 1699970),
milper = c(334, 394, 581, 2750, 581, 1789, 957),
tpop = c(131028, 47762, 41900, 79798, 44020, 170317, 71380),
cinc = c(0.182, 0.0997, 0.0396, 0.178, 0.0270, 0.138, 0.0591))
ratio
## # A tibble: 7 × 5
## country milex milper tpop cinc
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 USA 980000 334 131028 0.182
## 2 UKG 7895671 394 47762 0.0997
## 3 FRN 1023651 581 41900 0.0396
## 4 GMY 12000000 2750 79798 0.178
## 5 ITA 669412 581 44020 0.027
## 6 RUS 5984123 1789 170317 0.138
## 7 JPN 1699970 957 71380 0.0591Con las operaciones que vemos en el recuadro lateral, podemos responder preguntas como las siguientes:
Con las variables de ratio podemos hacer operaciones de:
- Igualdad (
==,%in%) - No igualdad (
!=) - Mayor que (
>) - Mayor o igual que (
>=) - Menor que (
<) - Menor o igual que (
<=) - Mínimos (
min()) y máximos (max()) - Sumas (
+), restas (-), multiplicaciones (*), divisiones (/) - Otros tipos de operaciones como raíces cuadradas (
sqrt()), logaritmos (log()), máximos (max()), mínimos (min()) o medias (mean()).
¿Qué país tiene más un personal militar superior al millón de personas?
ratio$country[ratio$milper > 1000]
## [1] "GMY" "RUS"¿Cuántas veces el gasto militar de Alemania es superior a cada una de las otras potencias?
ratio$milex_gmy <- ratio$milex[ratio$country == "GMY"] / ratio$milex¿Qué país tiene un personal militar inferior al 1 % de la población?
ratio$country[1 > ratio$milper / ratio$tpop * 100]
## [1] "USA" "UKG"¿Cuál es el país con el índice CINC más alto?
ratio$country[ratio$cinc == max(ratio$cinc)]
## [1] "USA"¿Cuál es el país con menos gasto militar?
ratio$country[ratio$milex == min(ratio$milex)]
## [1] "ITA"11.5.2 Importar variables de ratio
Las variables de ratio se suelen importar automáticamente como vectores numéricos, que es lo que necesitamos para realizar operaciones de todo tipo. Sin embargo , conviene saber distinguir entre tres tipos (u órdenes) de variables de ratio: los recuentos, las ratios y los índices compuestos (Merry, 2016, pág. 15; Power, 1999). Estos tipos de variables los encontramos representados en la siguiente tabla 11.7, que incluye datos de Eurostat y datos de voto en partidos regionalistas e independentistas en varias regiones europeas (Sanjaume-Calvet et al., n.d.).
| id | country | nuts_name | vote_reg | vote_ind | gdpc | innov | pop | density | area | distance |
|---|---|---|---|---|---|---|---|---|---|---|
| BE1 | Belgium | Région De Bruxelles-Capitale/Brussels Hoofdstedelijk Gewest | 13.81 | 26.31 | 68500 | 135.77406 | 1199095 | 7421.6 | 162 | 0.0384190 |
| BE2 | Belgium | Vlaams Gewest | 0.00 | 43.33 | 39800 | 132.69463 | 6526061 | 487.2 | 13599 | 0.2280460 |
| BE3 | Belgium | Région Wallonne | 4.14 | 0.00 | 28100 | 113.03631 | 3626571 | 215.3 | 16905 | 0.8535276 |
| BG324 | Bulgaria | Разград | 40.08 | 0.00 | 4600 | 34.15538 | 115402 | 47.6 | 2414 | 3.4172388 |
| BG425 | Bulgaria | Кърджали | 63.05 | 0.00 | 3900 | 33.53948 | 150837 | 47.7 | 3212 | 2.4012413 |
| CZ031 | Czech Republic | Jihočeský Kraj | 14.57 | 0.00 | 14800 | 77.76700 | 638782 | 66.5 | 10058 | 0.9911074 |
| CZ032 | Czech Republic | Plzeňský Kraj | 5.80 | 0.00 | 16700 | 77.76700 | 578629 | 77.0 | 7649 | 1.3294820 |
| CZ042 | Czech Republic | Ústecký Kraj | 2.46 | 0.00 | 13100 | 56.43587 | 821377 | 156.9 | 5339 | 0.7669622 |
| CZ071 | Czech Republic | Olomoucký Kraj | 0.75 | 0.00 | 14200 | 75.04677 | 633925 | 121.6 | 5273 | 2.7425572 |
| CZ072 | Czech Republic | Zlínský Kraj | 0.67 | 0.00 | 15600 | 75.04677 | 583698 | 149.2 | 3962 | 3.3911309 |
En este capítulo también hemos visto anteriormente en bases de datos ejemplos de variables de ratio. Por ejemplo:
- La duración de una disputa militar militarizada (duration) en la tabla 10.4.
- Los meses de un líder político al cargo (tenure_months) en la tabla 10.8.
- El tamaño relativo de un grupo étnico dentro de un país (size) en la tabla 10.6.
Los datos de recuento son datos que cuentan unidades, como la población (pop) o la superficie del territorio (area). Por definición, son datos que encontraremos sin decimales. Los datos de ratio, en cambio, son los que están creados a partir de dos números. Los más habituales son los datos de porcentaje, en los que el primer número es un recuento y el segundo es el total, como los datos de porcentaje de voto (voto_reg, que divide votantes a partidos regionalistas por el total de votantes). Pero también nos podemos encontrar datos de ratio en la densidad de población (density, compara habitantes y área) o el PIB per cápita (gdpc, establece la media de ingresos por habitante). Es muy probable que los datos de ratio tengan decimales. Finalmente, los índices son las medidas más complejas, puesto que agrupan varias variables, como por ejemplo el Índice de Innovación Regional (innov).