11 Tipos de visualizaciones
11.1 Introducción
Hasta ahora la explicación se ha focalizado en explicar las tres capas principales necesarias para generar gráficas con la función ggplot(). Se ha visto cómo, a partir de definir un marco de datos, indicando una proyección estética determinada y especificando una geometría se podía generar un mismo tipo de gráfica de formas muy diferentes. Se ha podido comprobar la versatilidad del paquete ggplot2 a la hora de mostrar los datos usando diferentes variantes en proyecciones estéticas y atributos. A pesar de todo, hasta en este punto, básicamente se ha cubierto un único tipo de gráfica: la gráfica de dispersión. Esta gráfica es una de las más habituales en ciencias sociales y nos ha permitido explorar la relación entre dos y más variables. Ahora bien, como se decía anteriormente, hay otros muchos tipos de geometrías para crear gráficas.
Este apartado desarrolla con más detalles las características de diferentes geometrías muy usuales a la hora de comunicar información. Un elemento que hay que tener en cuenta es que a la hora de representar gráficamente datos es esencial tener presente cuál es la naturaleza de la variable que se quiere representar. En función del tipo de variable, se tendrá que emplear una forma diferente de representación gráfica. En concreto, en este apartado se presentarán diferentes formas de elaborar gráficas descriptivas en función de si queremos representar una variable numérica o categórica o de si queremos combinar esta visualización con otra variable.
11.2 Una variable numérica
El principal tipo de gráfica que se utiliza para representar variables numéricas es el histograma. Esta geometría genera varias barras verticales que muestran la frecuencia (el número de veces) que se observa una unidad entre un determinado rango de valores de la variable de interés. La anchura de las barras del histograma comprende el intervalo de valores y la altura de la barra indica el número de casos que se producen en cada intervalo. Por defecto, cuando se genera un histograma, una función estadística automática separa los datos en diferentes intervalos y los apila por columnas. Una característica menos conocida de los histogramas es que el área de los rectángulos que conforman las barras es una representación proporcional a la cantidad que la gráfica está representando; por eso, la base (los intervalos de valores) y la altura deben tener, a la fuerza, unas unidades conocidas.
Para continuar con los ejemplos anteriores, se representará la distribución de valores de la variable innov de la base de datos nuts. Hasta ahora se había mostrado cómo se relacionaba esta variable con los niveles de satisfacción con el gobierno, pero antes de especificar las relaciones con otras variables siempre es recomendable mirar la distribución de cada variable por separado. Para generar un primer histograma, se aplicará la gramática de capas, tal como se había hecho hasta ahora, pero sustituyendo la geometría de puntos por la geometría específica de los histogramas: geom_histogram(). El histograma de la variable de innovación quedaría como vemos en la figura 11.1:
nuts |>
ggplot(mapping = aes(x = innov)) +
geom_histogram()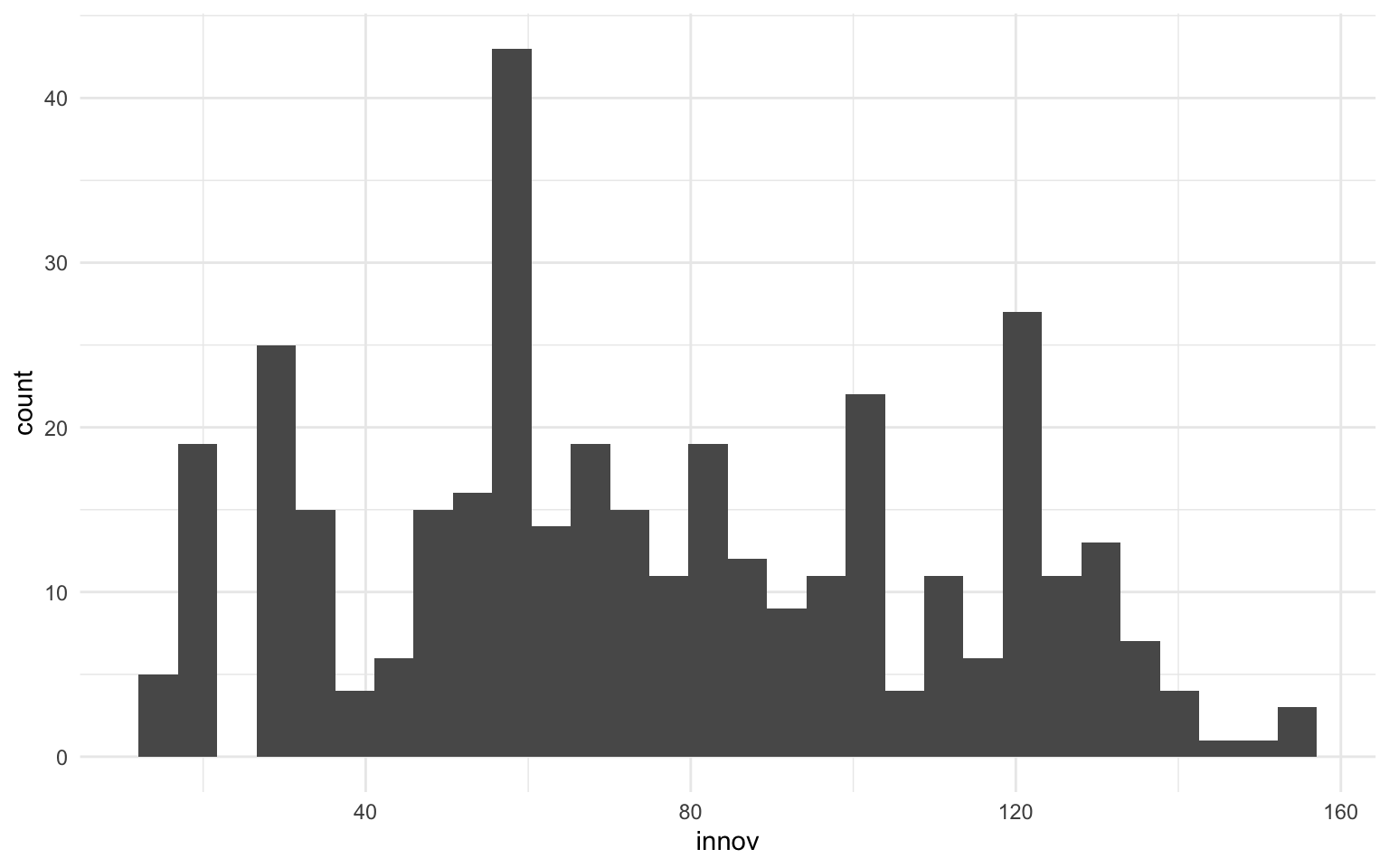
También se puede representar un histograma con un eje de las \(y\) en que, en lugar de las frecuencias absolutas, se presenten las frecuencias relativas o porcentajes. Simplemente hay que introducir el estético siguiente en la geometría: geom_histogram(aes(y = ..count../sum(..count..))).
nuts |>
ggplot(mapping = aes(x = innov)) +
geom_histogram(aes(y = ..count../sum(..count..)))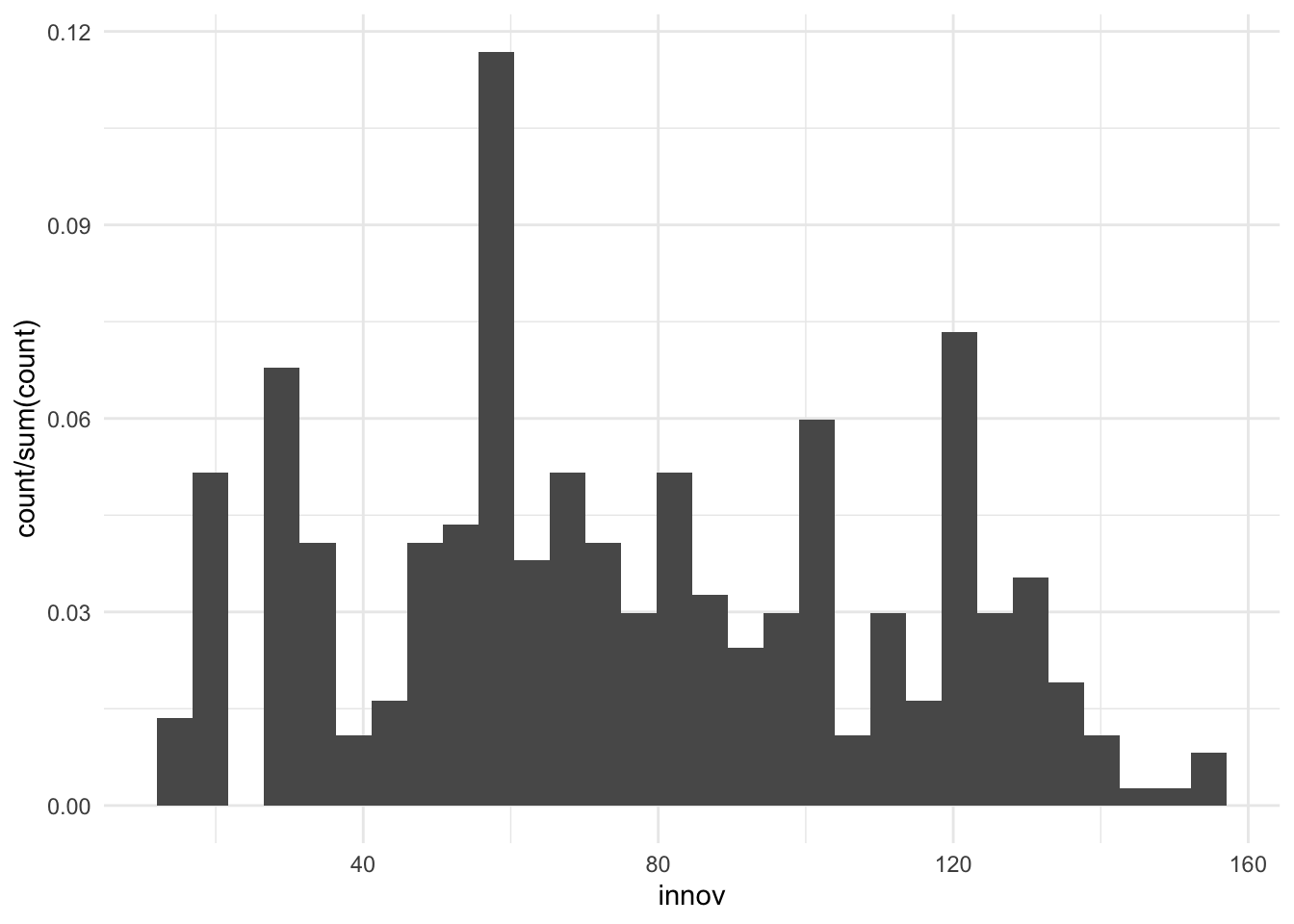
Un primer elemento que hay que destacar del código para elaborar la gráfica es que, en este caso, solo se ha indicado una única proyección estética: el eje de las \(x\), donde se ha definido la variable de interés. Como la base y los intervalos de valores de la variable innov es lo único que interesa, solo había que definir un único eje cartesiano. No hay que indicar el eje vertical de las \(y\), puesto que, si no se indica, por defecto muestra el recuento de casos de cada columna (las frecuencias). Si no se especifica lo contrario, el histograma corta la variable en 30 intervalos de la misma anchura y, como se ha dicho anteriormente, representa la cantidad de valores que hay en cada intervalo con la altura de las columnas. En el caso de la variable innovación, cada barra representa un intervalo de unos 5 puntos.
Solo observando la gráfica ya se puede identificar claramente que la moda —o clase modal, puesto que se trata de una variable continua— se concentra en los valores entre 55 y 60 puntos. Es en este rango de valores donde se concentran prácticamente 50 observaciones. En cambio, hay un intervalo (entre 20 y 25 aprox.) donde no hay ninguna observación. Como se decía anteriormente, por defecto ggplot2 divide los datos en 30 intervalos de datos. Estos intervalos también se pueden definir de manera manual. Se puede hacer de dos formas diferentes:
nuts |>
ggplot(aes(x = innov)) +
geom_histogram(bins = 6)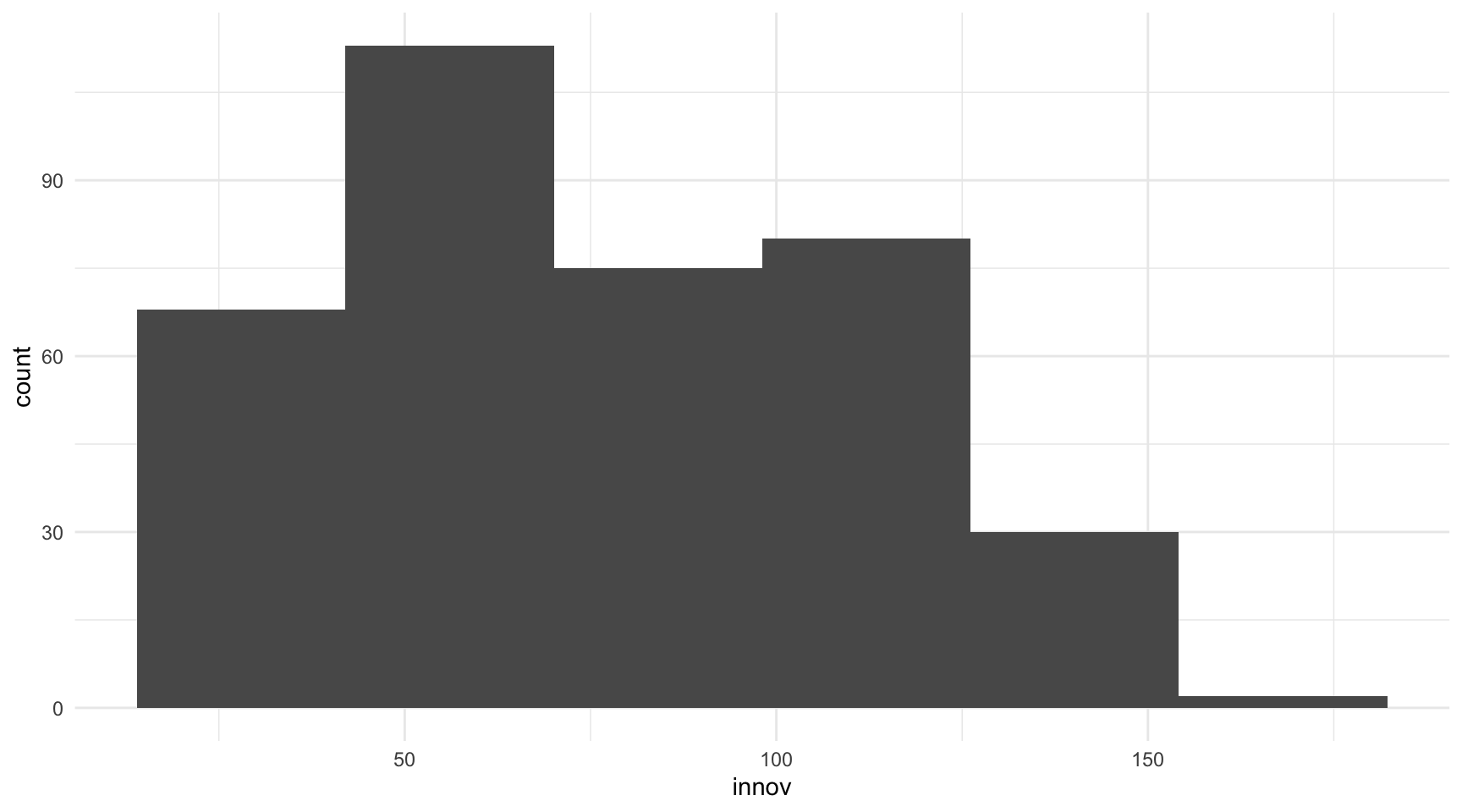
nuts |>
ggplot(aes(x = innov)) +
geom_histogram(binwidth = 3)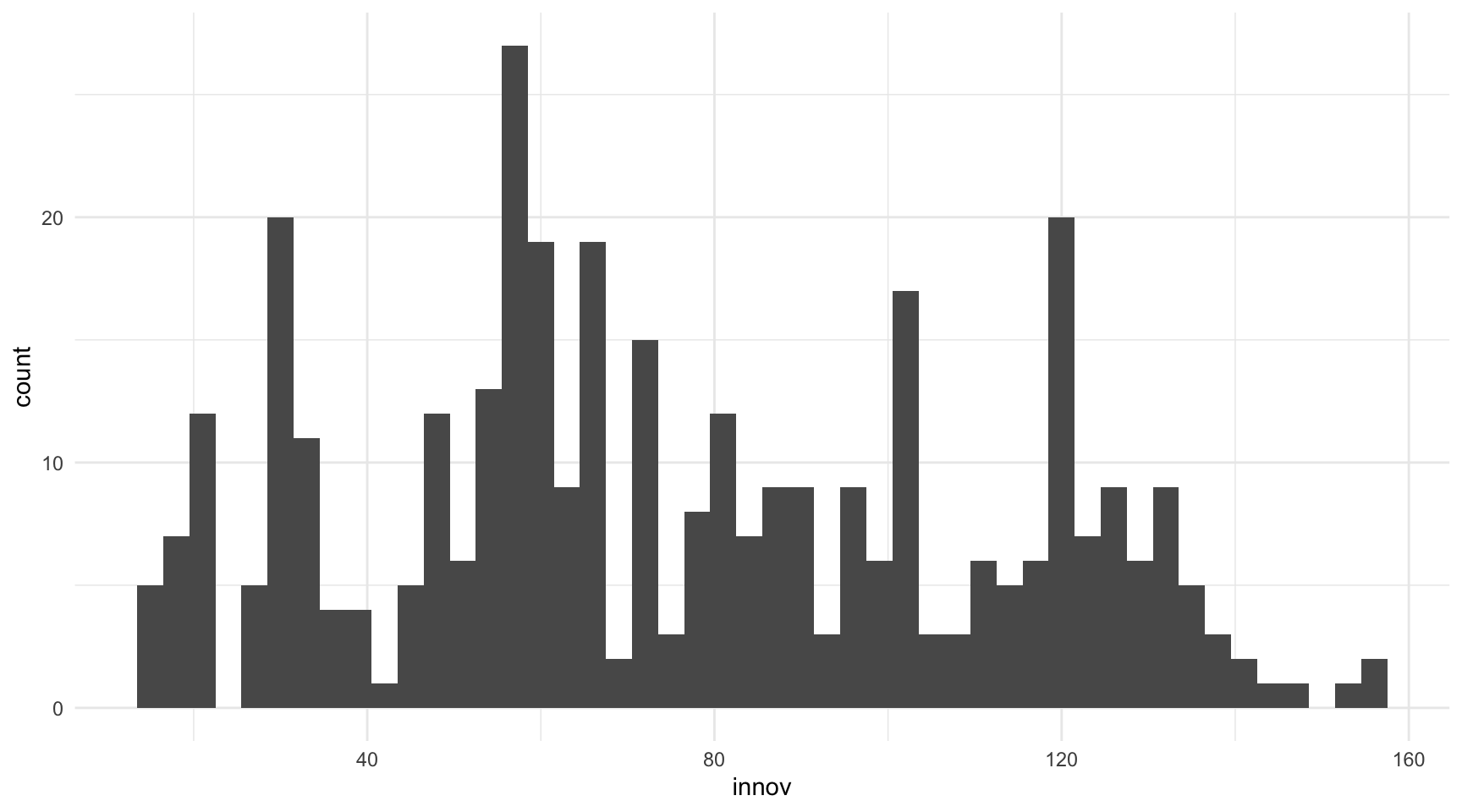
Bins: indicando la cantidad de intervalos concreta, es decir, el número de barras que se quiere que tenga el histograma. Para hacerlo, hay que añadir el argumento
binse indicar el número de intervalos (barras) deseado. En la figura 11.3 se indican seis intervalos.Binwidth: indicando la anchura de los intervalos, es decir, cuántas unidades tiene que medir la base de cada una de las barras. Por ejemplo, si en la variable
innovse quiere que cada barra represente conjuntos de 10 puntos en la variable innovación, se indicaría el número 10 en el argumentobinwidth(figura 11.4).
Más allá de la definición de las barras, se pueden usar otros atributos que se han visto anteriormente para mejorar la visualización del histograma. Por ejemplo, se puede cambiar el atributo del color de las barras con el argumento fill o el color del contorno de las barras con el argumento color. Finalmente, también puede ser interesante añadir una línea vertical que muestre el valor medio del nivel de innovación de las regiones europeas. Esto se podría hacer añadiendo una geometría con la función geom_vline() (vline, por vertical line) e indicando a la proyección estética cuál es el valor que se quiere incluir. A continuación, en la figura 11.5 se muestra un ejemplo de histograma con algunos cambios personalizados:
nuts |>
ggplot(mapping = aes(x = innov)) +
geom_histogram(binwidth = 10,
color = "black",
fill = NA) +
geom_vline(aes(xintercept = mean(innov, na.rm = TRUE)),
linetype = "dashed") 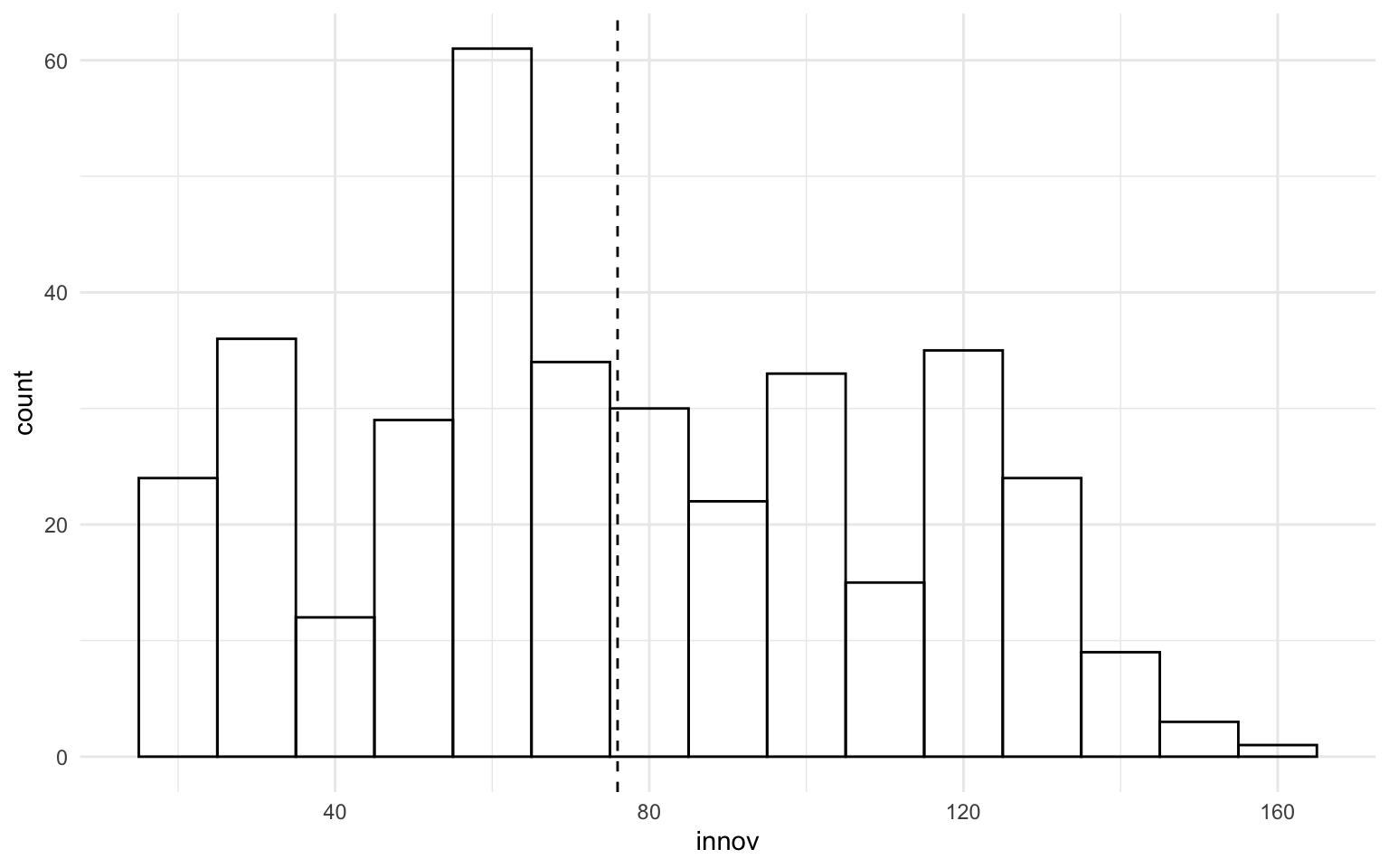
Como ya se ha visto anteriormente, el color como proyección estética puede ayudar a incorporar una nueva variable en una gráfica. En concreto, en un histograma puede ayudar a observar la distribución de valores de una variable en función de diferentes categorías en otra variable. En la gráfica siguiente, por ejemplo, se puede ver cuál es la distribución en los niveles de innovación de las regiones en función de si la región tiene mucha o poca población. Por eso, en la figura 11.6 hemos dicotomizado previamente la variable pop con la función if_else() en función de si cada región tiene más (Large) o menos (Small) de medio millón de habitantes.
nuts |>
mutate(pop = if_else(pop > 500000, "Large", "Small")) |>
ggplot(aes(x = innov, fill = pop)) +
geom_histogram()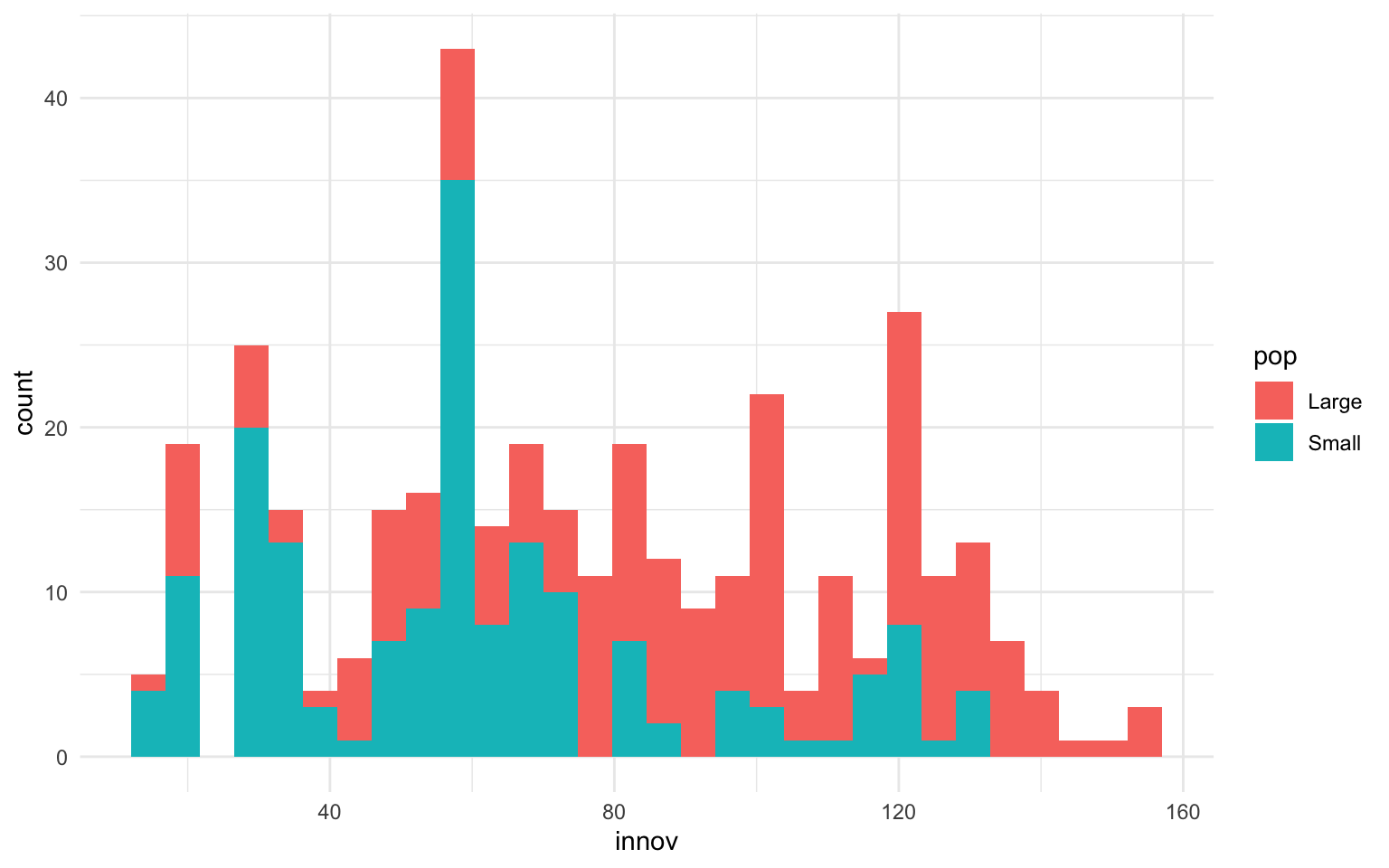
Todos estos cambios hechos en la visualización del histograma no hacen necesariamente que el histograma sea mejor. No hay una regla concreta, sino que la decisión sobre cuál es el mejor histograma estará condicionada por el objetivo de lo que se quiera comunicar. Por eso es tan importante, antes de ponerse a graficar, tener siempre muy claro qué es lo que se quiere transmitir y después decidir qué cambios hay que hacer para obtener la visualización que se quiere.
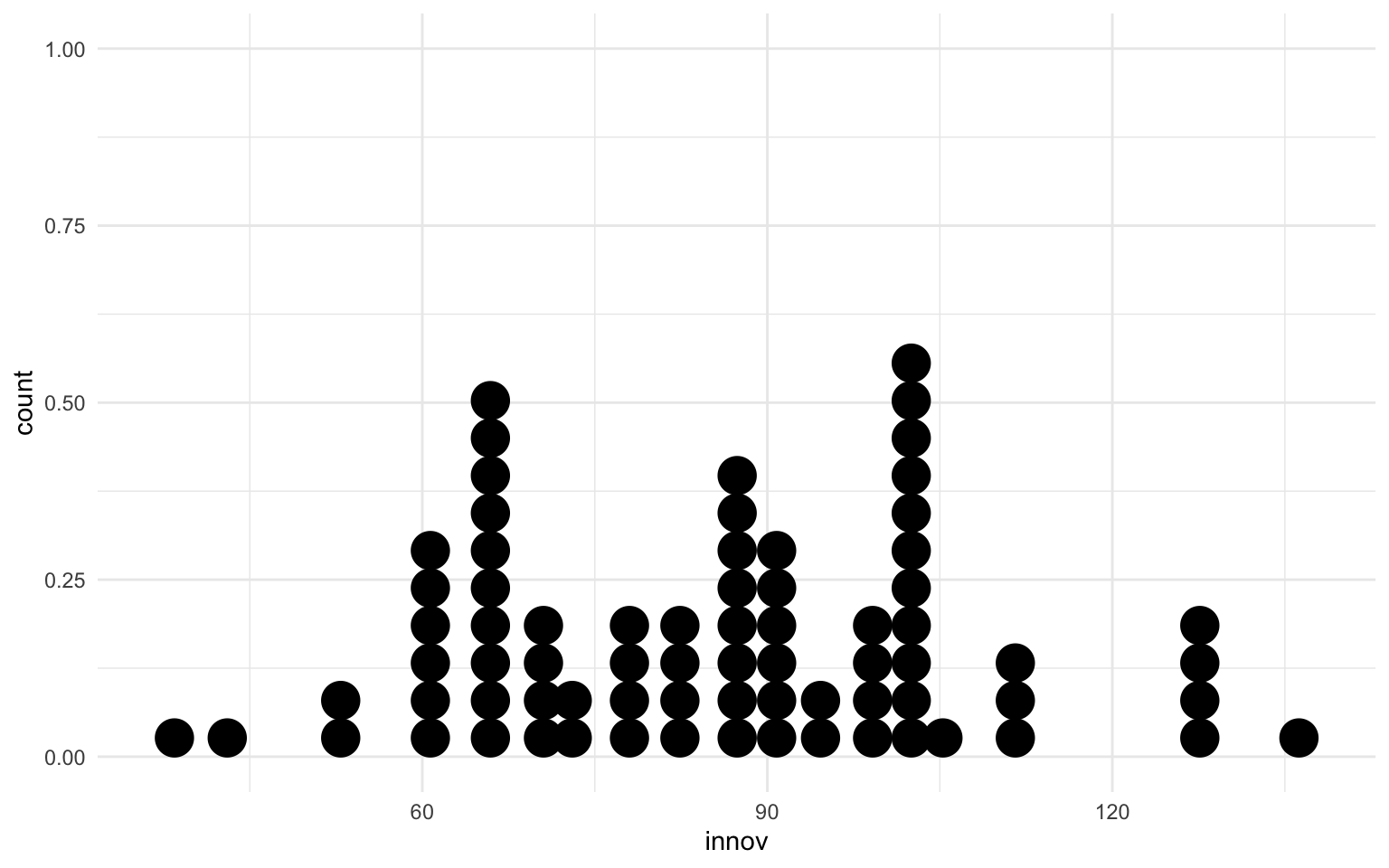
Alternativamente, podemos considerar otras opciones para graficar una variable numérica muy similares al histograma, como son el diagrama de densidad y el dotplot. Vemos un ejemplo de cada en la figura 11.7. Con el diagrama de densidad, priorizamos la visualización de la curva de la distribución, lo que permite añadir dentro de la gráfica información como la mediana o la media sin cargar visualmente la gráfica. El dotplot se acostumbra a utilizar cuando no disponemos de muchos datos, o bien los datos numéricos están agrupados en un número discreto de categorías.
Muestra el código
nuts |>
ggplot(aes(x = innov)) +
geom_density() +
geom_vline(aes(xintercept = mean(innov, na.rm = TRUE)),
col = "blue", linetype = "dashed") +
geom_vline(aes(xintercept = median(innov, na.rm = TRUE)),
col = "green", linetype = "dashed")
nuts |>
filter(ccode %in% c("ES", "FR", "IT", "PT", "GR") ) |>
ggplot(aes(x = innov)) +
geom_dotplot()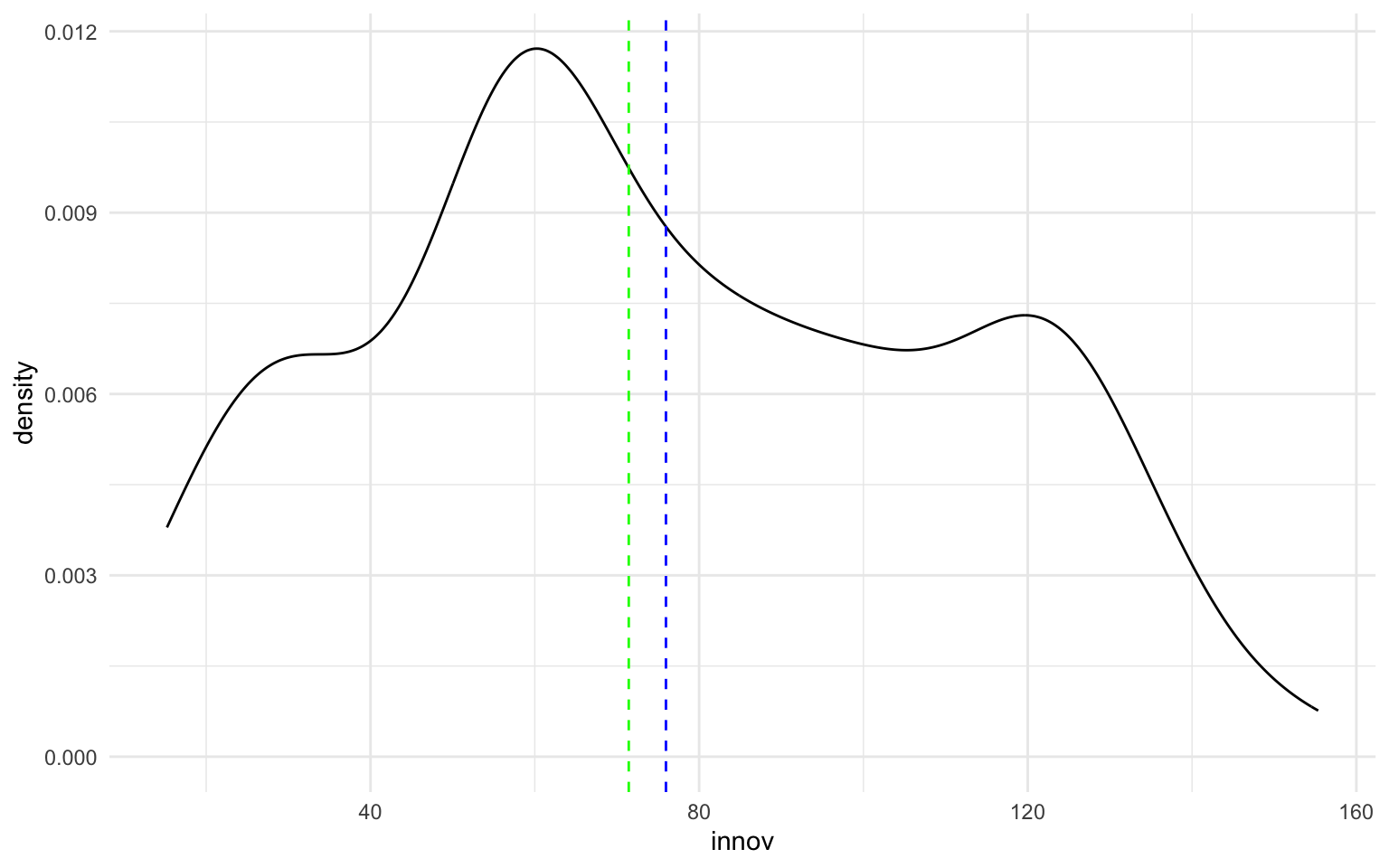
11.3 Una o dos variables categóricas
Si lo que se quiere es graficar una variable de tipo categórico, una opción es elaborar un diagrama de barras. Esta gráfica, a pesar de que se puede parecer a un histograma, está pensada únicamente para variables cualitativas en las que cada barra hará referencia a una de las categorías de la variable. En cambio, en el histograma, como ya se ha visto, las barras agrupan diferentes rangos de valores de una variable cuantitativa. Si bien en ambos casos la altura de la barra hace referencia al número de casos, la forma en la que se definen las barras es lo que distingue de forma crucial ambos tipos de gráficas.
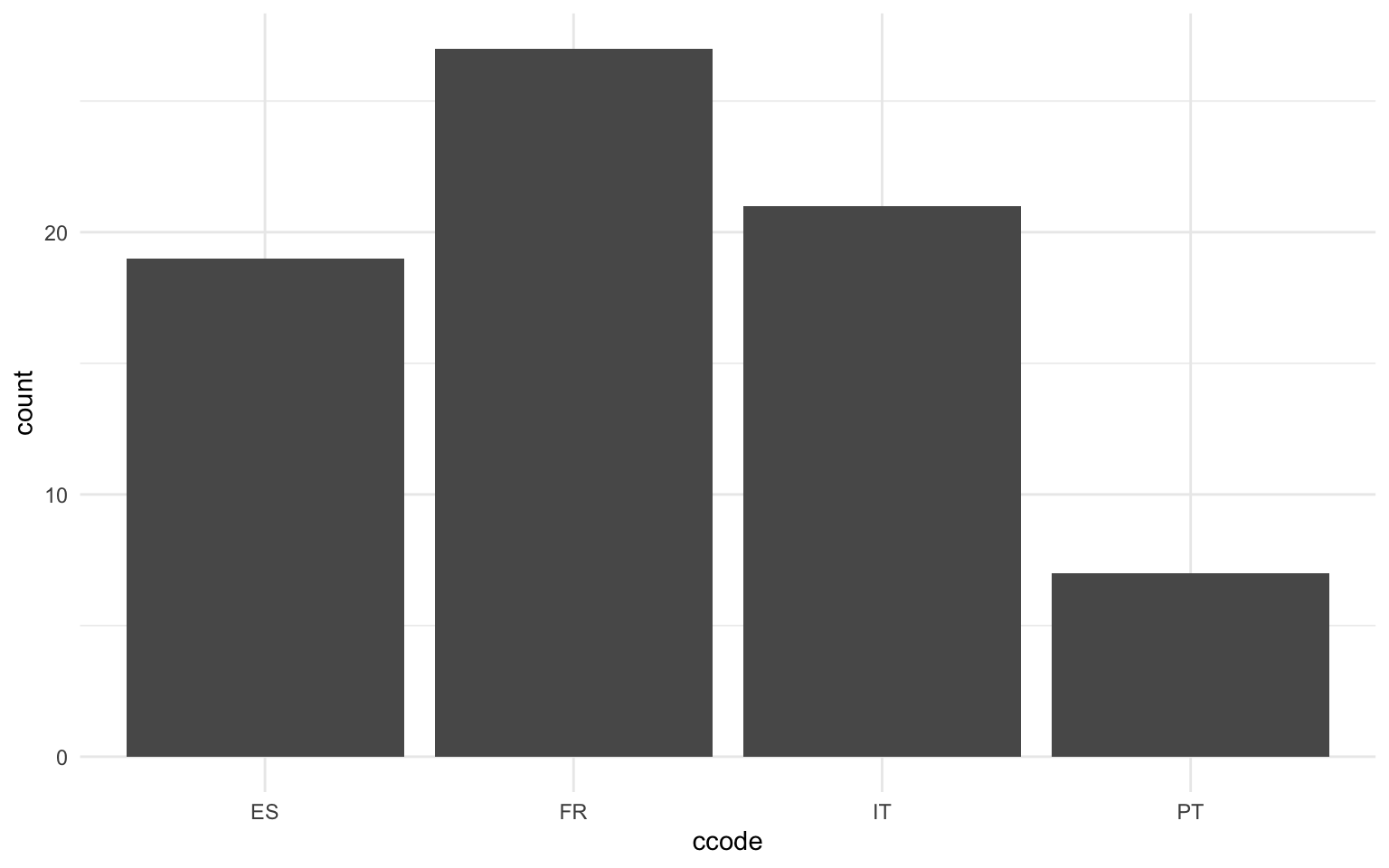
Para empezar, es importante remarcar que existen diferentes tipos de diagramas de barras. El más básico, que veremos en esta subsección, es la gráfica de barras que muestra las frecuencias de cada categoría. En esta gráfica lo único que se tiene que indicar en la proyección estética es la variable \(x\), que corresponderá a la variable categórica que se quiera recontar. A continuación, se usa la geometría geom_bar() para representar el diagrama, y, de manera automática, ggplot2 interpreta que lo que se quiere obtener es el recuento de veces que se repite cada una de las categorías. La figura 11.8 muestra el número de observaciones (número de regiones) en la base de datos por países (ccode), y, para facilitar la legibilidad de la gráfica, se ha optado por reducirlo a solo un conjunto de países de la base de datos. Esta gráfica muestra de forma descriptiva el número de regiones en cada uno de cuatro países europeos. Claramente, Francia, con 30 regiones, es el país que tiene más, seguido de Italia, España y Portugal.
Otra opción para graficar variables cualitativas es el diagrama de quesitos. La geometría asociada es exactamente la misma que para hacer un diagrama de barras, pero añadiendo una capa con la función coord_polar("y", start=0).
En las gráficas de barras podemos incluir una segunda variable categórica si pintamos las barras con un color que represente un estético. Esto se consigue indicando el vector de carácter o factor en cuestión en el argumento fill. En las tres gráficas siguientes de la figura 11.9 observamos qué observaciones de cada país están por debajo y por encima de la media de cada país. En el código siguiente primero se ha modificado el marco de datos para obtener una variable categórica que indique “Por encima” si el PIB per cápita de la región en cuestión está por encima de la media del país, y “Por debajo” si es lo contrario. Con este nuevo marco, se ha indicado que las categorías tenían que ser los países y la nueva variable gdp_above tenía que ocupar el argumento fill. Las tres gráficas muestran exactamente los mismos datos pero con las barras dispuestas de forma diferente.
Muestra el código
nuts |>
filter(ccode %in% c("ES", "FR", "IT", "PT")) |>
mutate(gdp_above = if_else(gdpcap_nuts > gdpcap_ctr, "Por encima", "Por debajo")) |>
ggplot(aes(x = ccode, fill = gdp_above)) +
geom_bar()
nuts |>
filter(ccode %in% c("ES", "FR", "IT", "PT")) |>
mutate(gdp_above = if_else(gdpcap_nuts > gdpcap_ctr, "Por encima", "Por debajo")) |>
ggplot(aes(x = ccode, fill = gdp_above)) +
geom_bar(position = "dodge")
nuts |>
filter(ccode %in% c("ES", "FR", "IT", "PT")) |>
mutate(gdp_above = if_else(gdpcap_nuts > gdpcap_ctr, "Por encima", "Por debajo")) |>
ggplot(aes(x = ccode, fill = gdp_above)) +
geom_bar(position = "fill")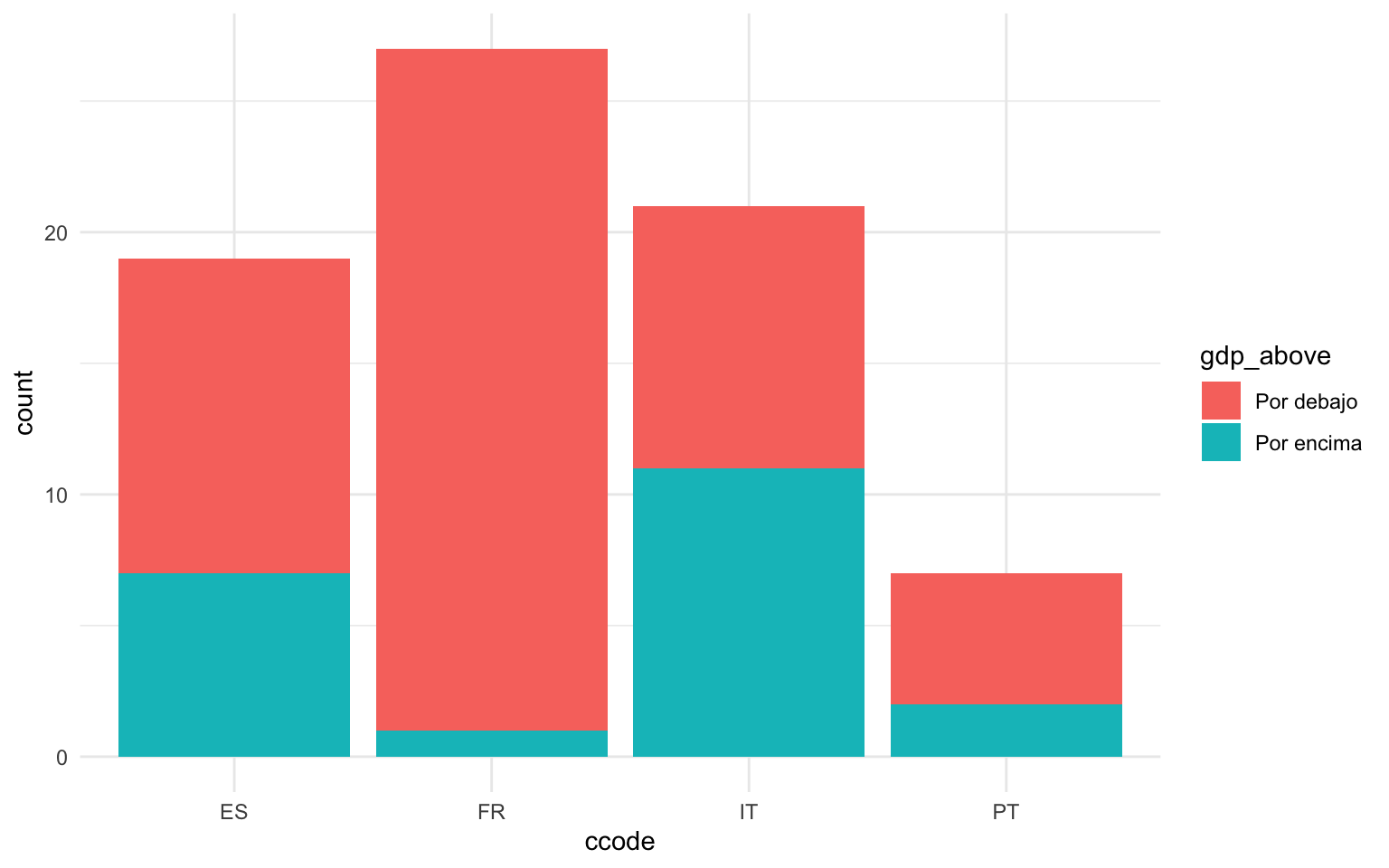
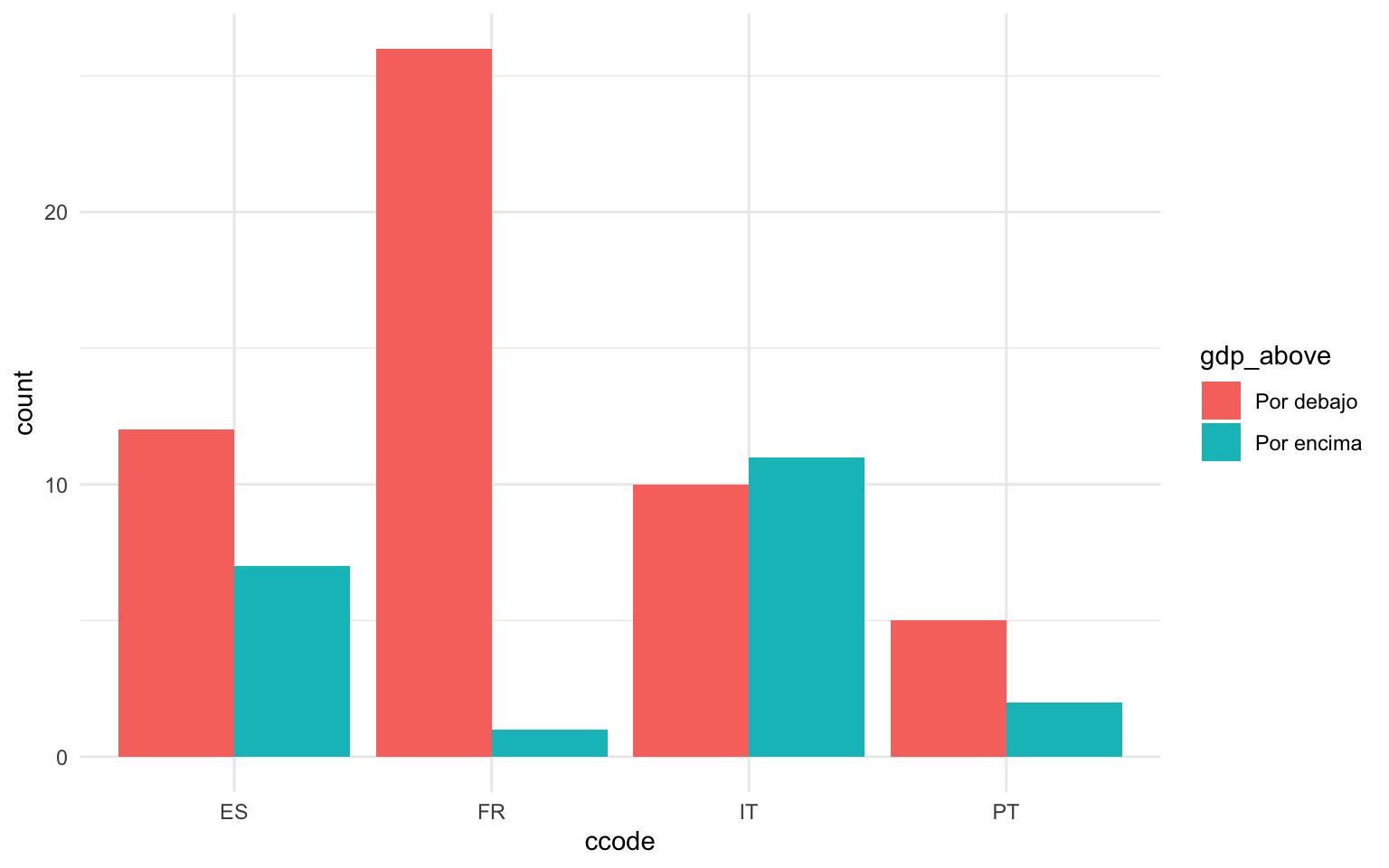
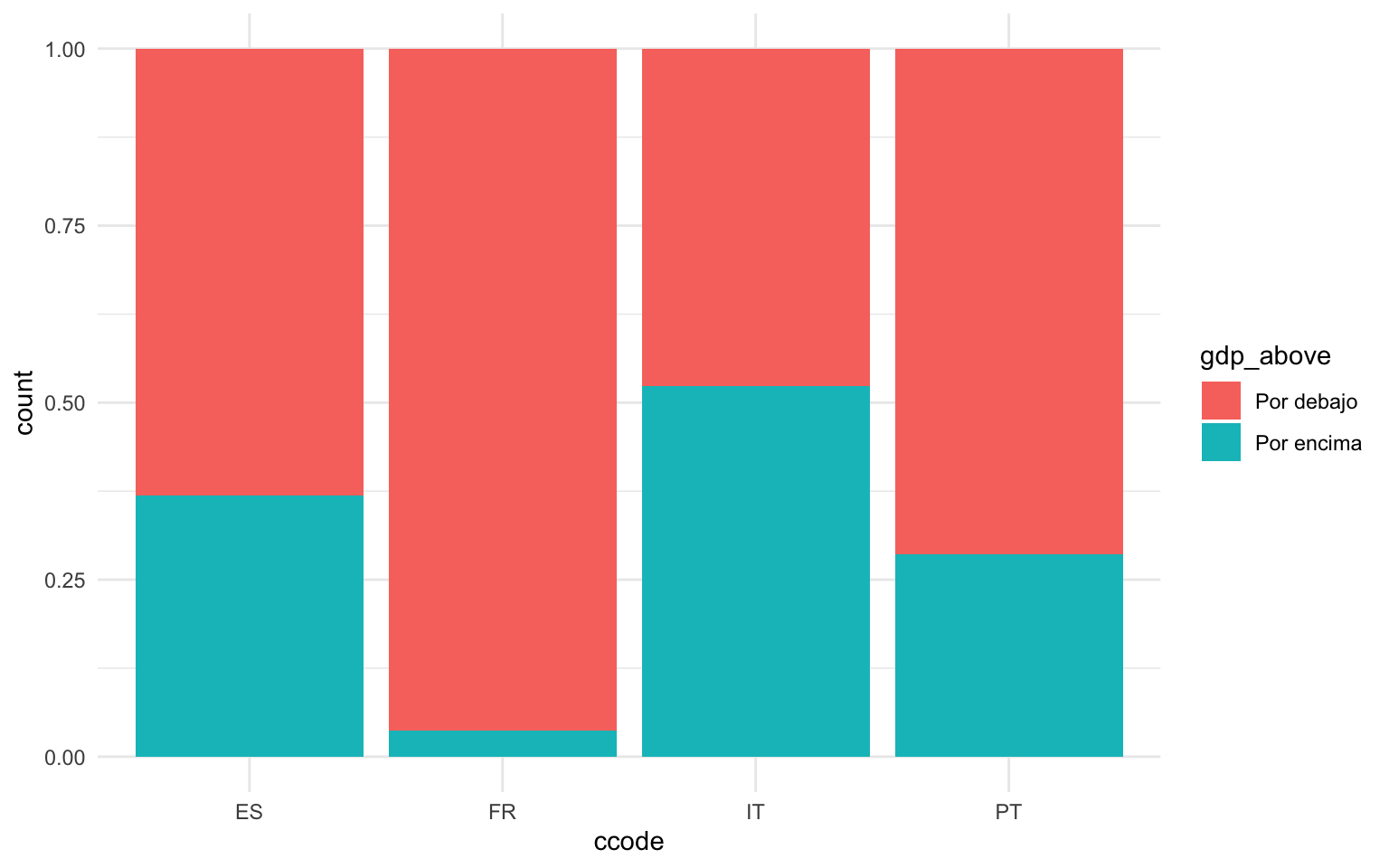
En la primera gráfica simplemente vemos apilados los datos del recuento, con los datos pintados de diferente color según los valores de la variable gdp_above. En la segunda gráfica, con el argumento position = "dodge" conseguimos que las barras estén una junto a la otra, de forma que nos pueda ser más fácil compararlas entre sí. Finalmente, en la última gráfica el argumento position = "fill" estira cada una de las barras de forma que todas tengan la misma longitud. Esto nos permite comparar las proporciones. Observamos que en Francia prácticamente todas las regiones tienen un PIB per cápita inferior a la media del país.
11.4 Una variable numérica según los valores de una categórica
Una segunda opción a la hora de generar un diagrama de barras sería combinar las categorías de una variable categórica (las barras) con el valor en una variable numérica. El valor de esta variable cuantitativa puede ser la media, la mediana o cualquier otro estadístico descriptivo. Para poder generar esta gráfica, es necesario, sin embargo, trabajar antes con funciones del paquete dplyr para resumir los datos que nos interesan. Generalmente, se hará uso de las funciones group_by() y summarise(). Además, a diferencia de la gráfica anterior, la geometría no sería geom_bar(), sino geom_col(). Esto es así porque lo que se busca no es el recuento de casos, sino que las barras del eje \(x\) estén asociadas a valores del eje \(y\). Se puede ver la implementación a partir del caso siguiente. Por ejemplo, si en lugar de querer graficar el número de regiones por país se quisiera graficar el valor medio de la satisfacción con el gobierno de las diferentes regiones del país, una manera de hacerlo sería la que observamos en la figura 11.10.
nuts |>
filter(ccode %in% c("ES", "FR", "IT", "PT")) |>
group_by(ccode) |>
summarise(stfgov = mean(stfgov,na.rm = T)) |>
ggplot(aes(x = ccode, y = stfgov)) +
geom_col()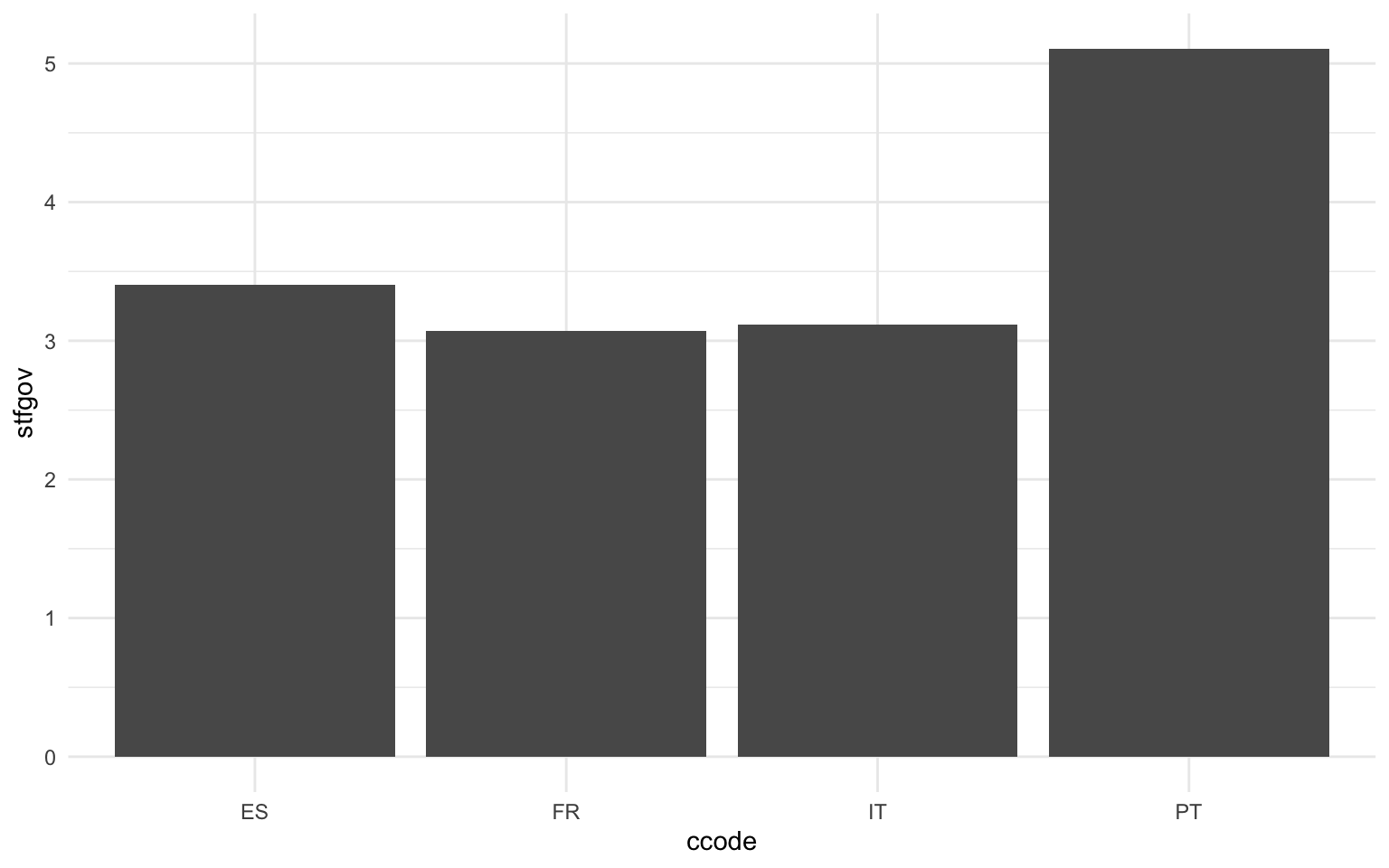
La gráfica anterior nos muestra que la satisfacción media con el gobierno es ligeramente superior a 3 en España, Francia e Italia, mientras que en Portugal es superior a 5. Para llegar a estas conclusiones, primero se ha filtrado la base de datos en los cuatro países de interés, se ha especificado que se querían agrupar las observaciones por país y, acto seguido, se ha resumido la variable stfgov a partir del cálculo de su media. Una vez resumidos los datos en un nuevo marco de datos, la función ggplot() ha permitido graficar como categorías los países y como valores la media de satisfacción con el gobierno.
Por otro lado, el diagrama de cajas también es una variable que nos ayuda a observar la distribución de una variable numérica según los valores de una variable categórica. De manera similar al histograma, permite visualizar alrededor de qué valores se concentran la mayoría de las observaciones y, a pesar de que no permite afinar tanto en relación con valores concretos, transmite de forma muy directa información sobre algunos estadísticos descriptivos clave. Para empezar, la caja del diagrama nos indica los valores donde se sitúan los cuartiles 1 y 3, es decir, a partir de qué valor se encuentra el 25 % de observaciones (Q1) y a partir de qué valor se encuentra el 75 % de observaciones (Q3). La distancia entre Q1 y Q3 define el rango de valores donde se encuentra el 50 % de todas las observaciones y es lo que se conoce como rango intercuartílico. La línea gruesa dentro de la caja indica donde se sitúa la mediana. Los bigotes que salen de la caja tienen una longitud máxima de 1.5 veces el rango intercuartílico. Ahora bien, si el valor mínimo queda por debajo de la longitud máxima del bigote, el bigote acaba en el valor más bajo de la distribución, y lo mismo pasa con el valor máximo. Si, en cambio, el valor mínimo queda fuera, cualquiera de las observaciones fuera de los bigotes se indicará con un punto y es lo que se conoce como una observación atípica (outlier). A ggplot2 los diagramas de cajas se indican con la geometría geom_boxplot(); la gráfica siguiente muestra un diagrama de cajas de la variable de satisfacción con el gobierno en cuatro países diferentes.
nuts |>
filter(ccode %in% c("ES", "FR", "IT", "PT")) |>
ggplot(aes(x = country, y = stfgov)) +
geom_boxplot()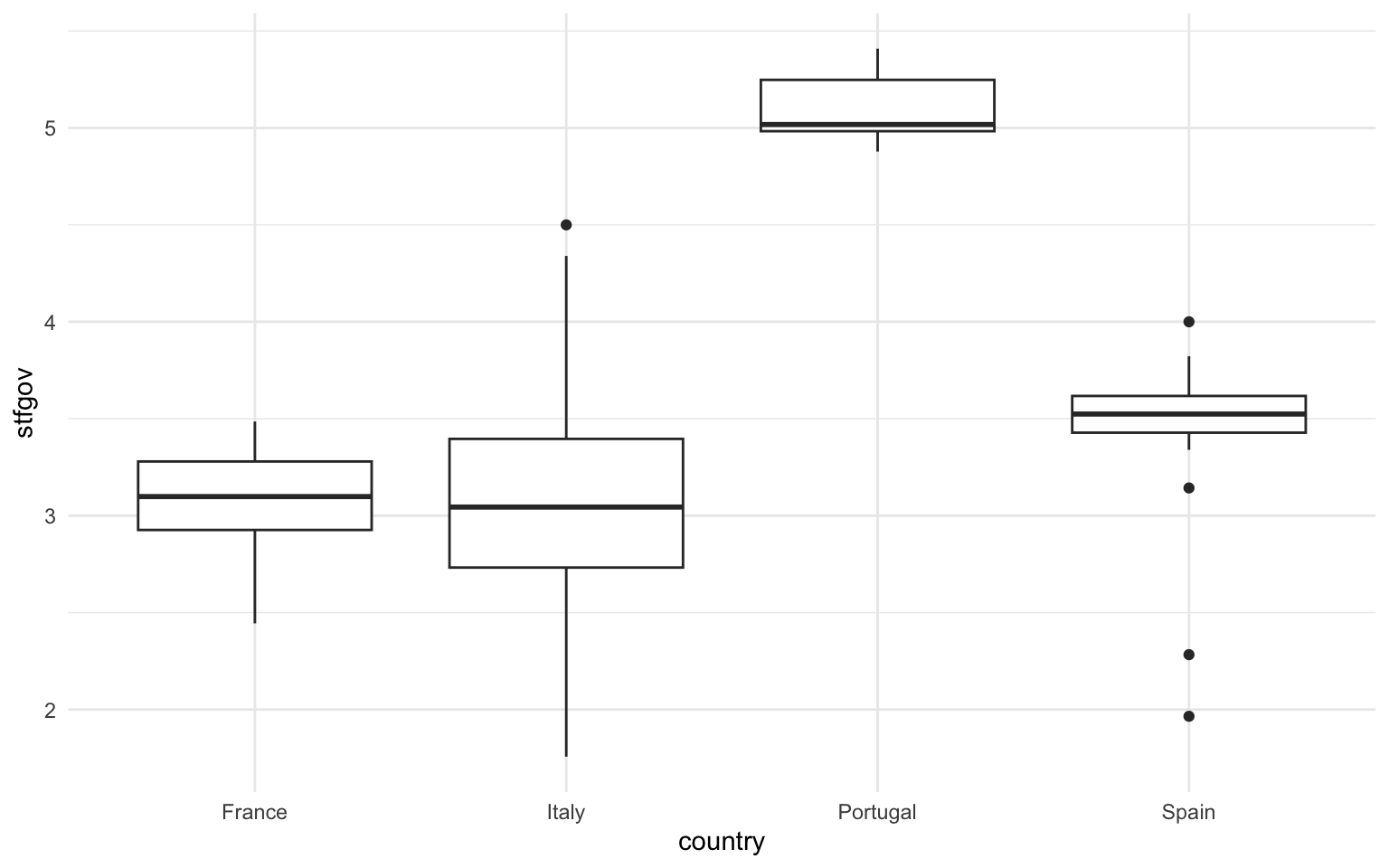
Como vemos en la figura 11.11, el país con una satisfacción mayor con el gobierno es Portugal. La mediana está cerca de 5 y no encontramos muchas diferencias entre el valor máximo y el valor mínimo, lo que significa que entre las regiones de Portugal hay una opinión parecida respecto al gobierno. En cambio, en Italia y en Francia la mediana está muy por debajo de Portugal, cerca de 3. La diferencia entre estos dos países es que en Italia hay mucha más dispersión entre regiones en cuanto a la satisfacción sobre su gobierno. En España la mediana se sitúa cerca de 3.5. Si bien la mayoría de las regiones tienen una opinión parecida, tal como indica el hecho de que hay muy poca distancia entre la parte superior y la parte inferior de la caja, también es cierto que hay algunos casos extremos: una región que tiene una opinión mucho más positiva que el resto y tres regiones que tienen una opinión mucho más negativa que el resto.
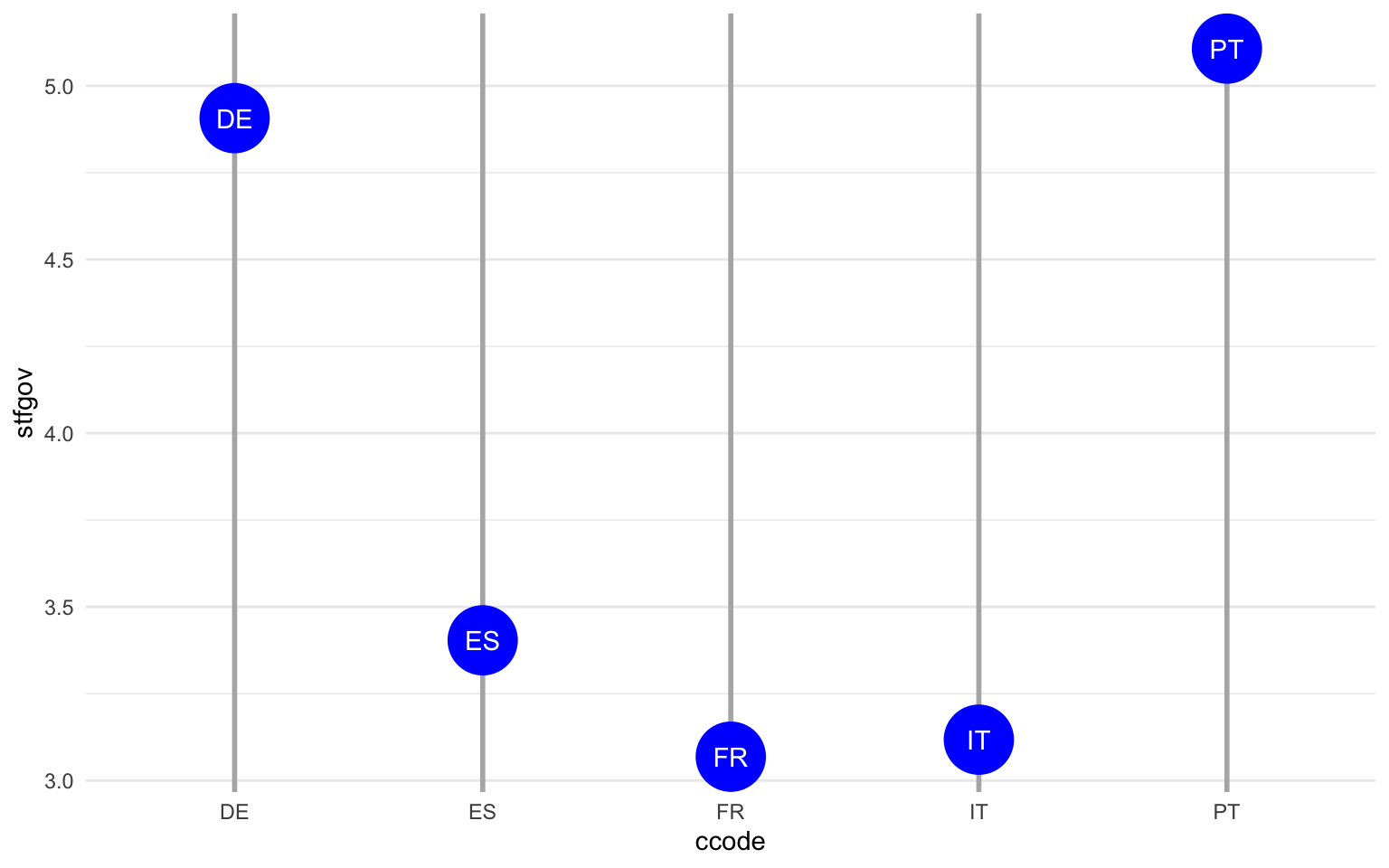
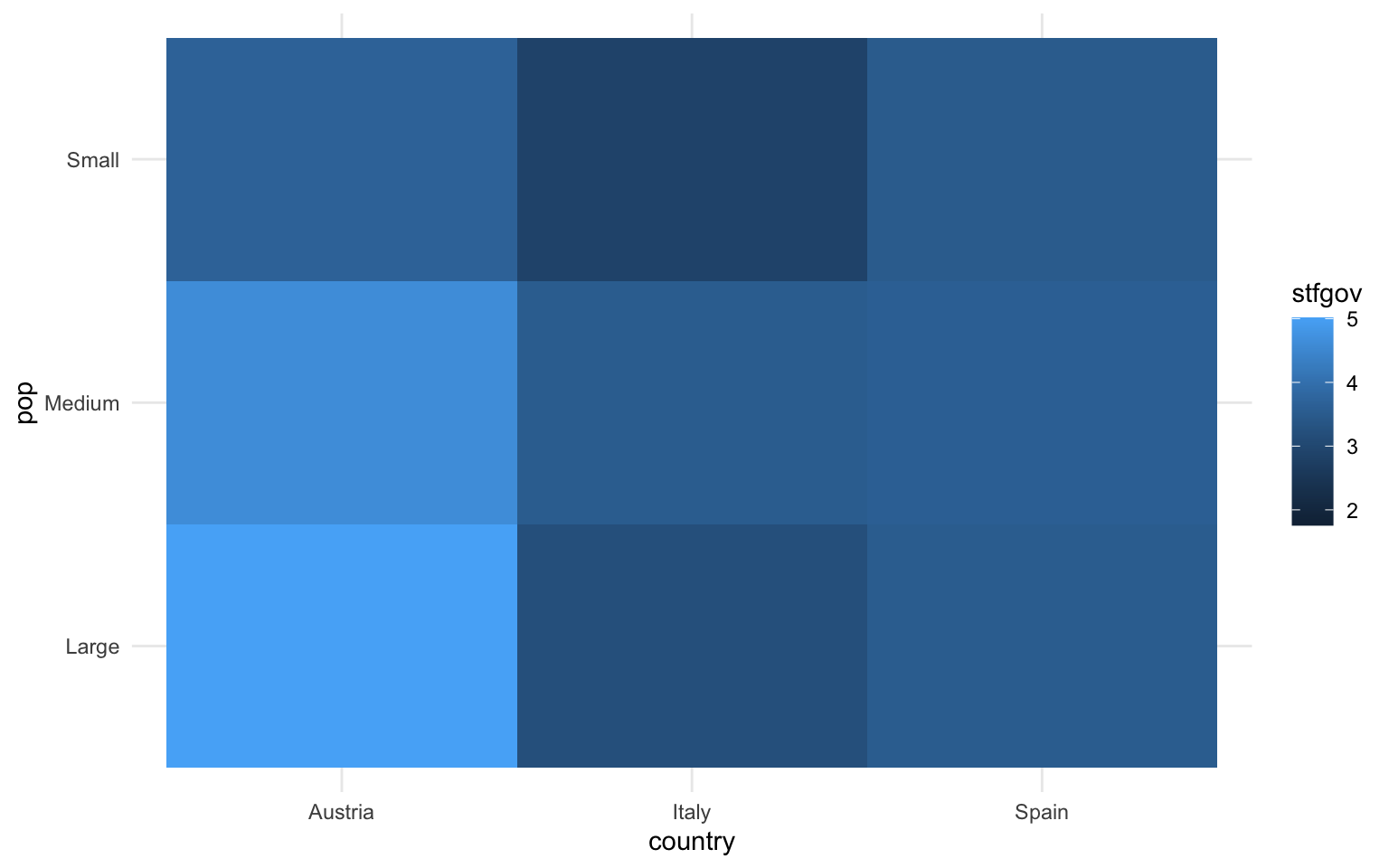
Aparte del diagrama de barras y el diagrama de cajas, hay otras maneras que nos permiten visualizar los valores de una variable numérica según los valores de una variable categórica. En la figura 11.12 vemos tres ejemplos. En la gráfica de la izquierda vemos un diagrama de violines, muy parecido al diagrama de cajas pero que prioriza la atención de la visualización en la distribución de casos en lugar de enfocarse en algunos estadísticos como la mediana o los valores del rango intercuartílico1. En la gráfica del medio observamos una combinación de geometrías de puntos y texto, que permite concentrar la visualización en un punto de tendencia central —en este caso la media, pero se podría calcular la mediana—, y un texto corto que permite identificar la observación. Finalmente, la gráfica de la derecha se conoce como diagrama de rectángulos y permite la visualización de una variable numérica en función de dos variables categóricas. En el ejemplo, en las regiones con mucha población de Austria es donde encontramos más satisfacción con el gobierno, mientras que en Italia hay insatisfacción con el gobierno en las regiones con poca población y mucha población.
1 El código de esta función incluye la función fct_reorder(), del paquete forcats, que permite que las categorías se vean de forma ascendente o descendente según los valores de la variable numérica. La función consta de tres argumentos: la variable categórica, que irá en el eje; los valores de la numérica de referencia, y el estadístico, que servirá para ordenar las categorías.
Muestra el código
nuts |>
filter(ccode %in% c("ES", "UK", "IT", "DE")) |>
ggplot(aes(x = fct_reorder(country, innov, median), y = innov)) +
geom_violin()
nuts |>
filter(ccode %in% c("ES", "FR", "IT", "PT", "DE", "PT")) |>
group_by(ccode) |>
summarize(stfgov = mean(stfgov, na.rm = T)) |>
ggplot(aes(x = ccode, y = stfgov, label = ccode))+
geom_point(size = 13, col = "blue") +
geom_text(col = "white") +
theme(panel.grid.major.x = element_line(size = 1, color = "grey70"))
nuts |>
filter(ccode %in% c("ES", "IT", "AT")) |>
mutate(pop = case_when(pop > 1000000 ~ "Large",
pop > 500000 ~ "Medium",
.default = "Small")) |>
ggplot(aes(x = country, y = pop, fill = stfgov)) +
geom_tile()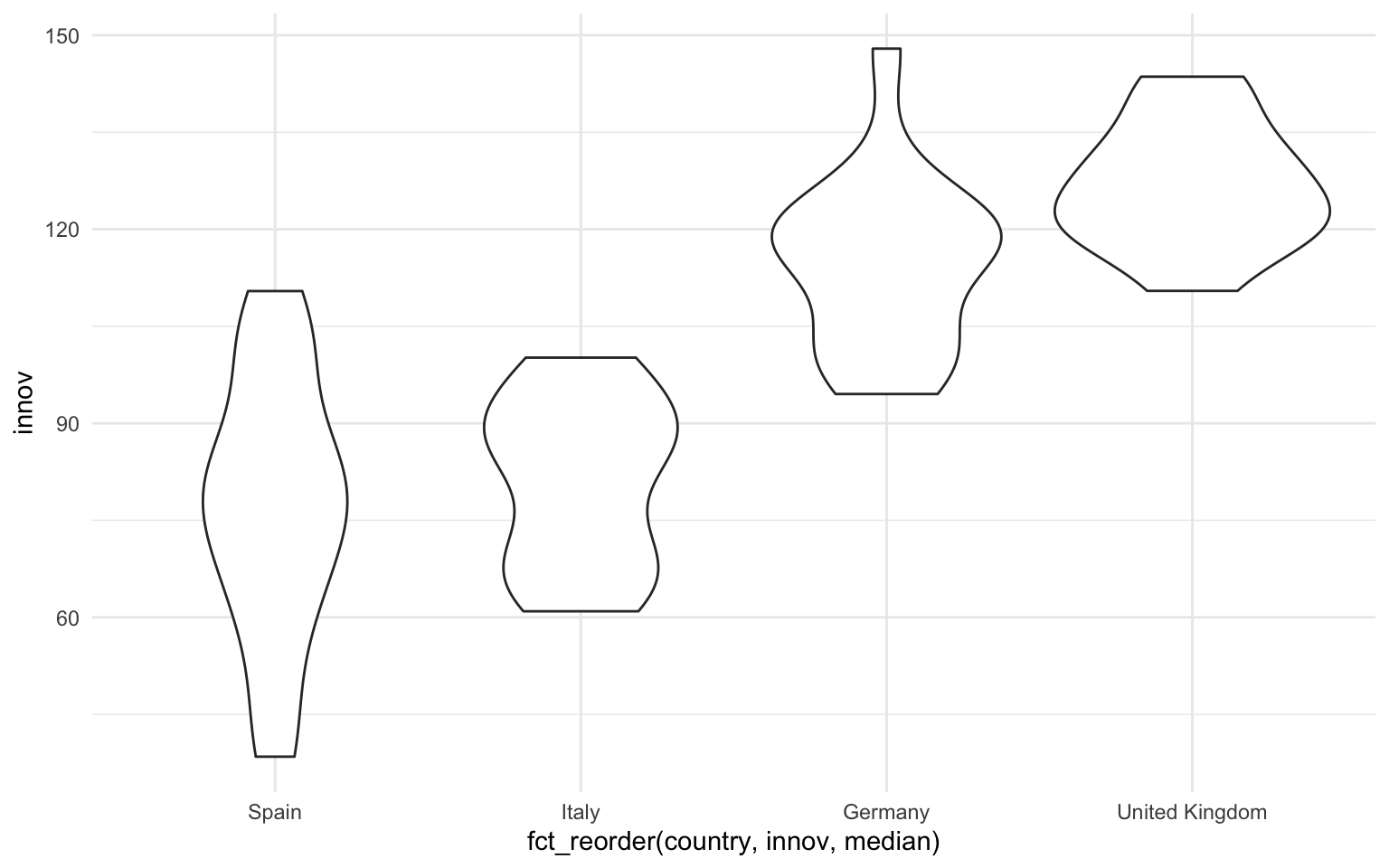
11.5 Variable numérica en el tiempo
Otra de las gráficas relevantes es el diagrama de líneas. Esta gráfica se utiliza generalmente para representar la evolución de diferentes categorías respecto a una variable numérica o cuantitativa a lo largo del tiempo. Por definición, son gráficas que requieren tres variables para poder ser representadas. A grandes rasgos, en el eje de las \(x\) suele haber una variable que indica temporalidad, a pesar de que también puede ser una variable categórica cualquiera; en el eje de las \(y\), una variable de tipo cuantitativo, y las diferentes líneas representan otra variable de tipo categórico. La función que permite incorporar la capa de geometría de línea a ggplot2 es geom_line().
Para poder trabajar con una serie temporal, en este apartado se trabajará con la base de datos de la WVS, que agrupa los resultados de diferentes encuestas similares a lo largo de diferentes oleadas en el tiempo. En concreto, se evaluarán las respuestas de una pregunta de la encuesta que pedía poner una nota de 0 a 10 a la satisfacción con la vida de los encuestados. Estas encuestas se han ido realizando en un gran número de países del mundo a lo largo del tiempo. Para simplificar los resultados, se ha optado por seleccionar una muestra de países, y la gráfica siguiente muestra los resultados.
wvs |>
filter(country %in% c("IRN", "JPN", "MEX", "SRB", "SWE", "THA", "USA", "ZAF")) |>
group_by(country, year) |>
summarise(stflife = mean(stflife,na.rm = T)) |>
ggplot(aes(x = year, y = stflife, color = country)) +
geom_line()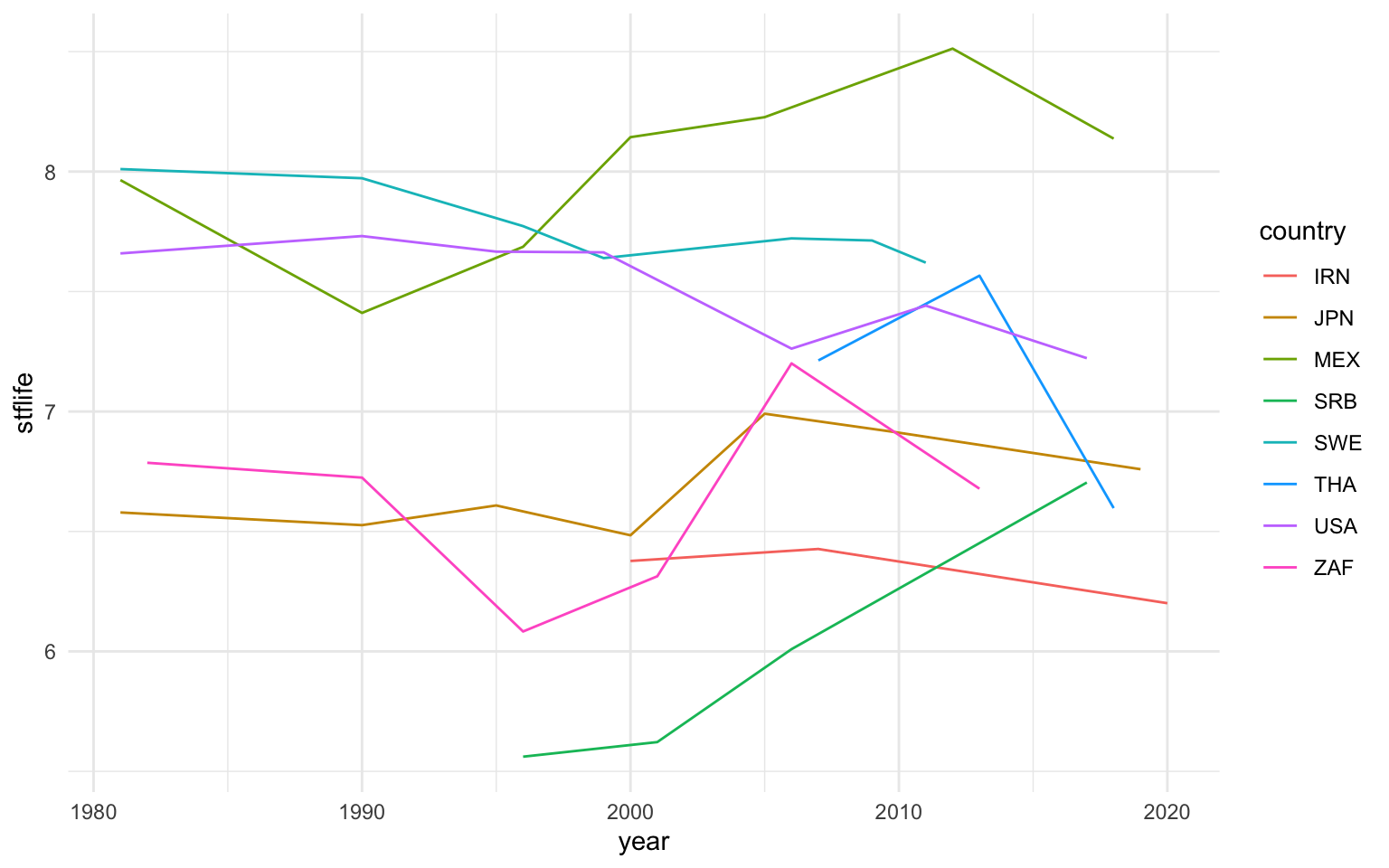
El código para poder hacer esta gráfica nos ha requerido hacer una transformación de la base de datos original, primero seleccionando los países de interés y después, para tenerla al nivel adecuado, con la agregación al nivel que se quiere (país-año). Una vez hecha esto, se ha obtenido la media de satisfacción con la vida para cada país-año de acuerdo con las encuestas de la WVS y se ha graficado con ggplot2, indicando que el año era la variable del eje \(x\), media de satisfacción con la vida la variable del eje \(y\), y que se quería distinguir los datos de cada país por colores. Finalmente, con la geometría geom_line(), se ha generado una gráfica de líneas que nos muestra la evolución de esta variable por países. En esta gráfica se puede ver que el país con más satisfacción con la vida es México, que superó Suecia a partir de mediados de los años noventa. Se puede comprobar que la satisfacción con la vida no es un elemento estático y que difiere entre países y evoluciona dentro de los países, posiblemente vinculado con acontecimientos políticos y económicos de relevancia que ocurren en el país. Por ejemplo, se puede entender fácilmente que Serbia fuera uno de los países con menos satisfacción a mediados de los noventa, cuando hacía poco tiempo del final de la guerra de los Balcanes, y cómo este indicador ha ido aumentando a lo largo del tiempo a medida que aumentaba el bienestar económico y se reducían las tensiones regionales.
Este tipo de gráficas de líneas a veces puede ser interesante combinarlo con una capa de geometría de puntos. La WVS no se hace exactamente el mismo año en todos los países, y añadir puntos a la gráfica puede ayudar a situar mejor en qué años se llevaron a cabo las encuestas. Finalmente, cuando se trabaja con gráficas de líneas, el mejor estético para diferenciar diferentes categorías es el color, aunque también se podría utilizar el tipo de línea (linetype) o una combinación de color y tipo de línea. El número de categorías será habitualmente el elemento que condicionará la elección y modificación de la proyección estética.
wvs |>
filter(country %in% c("IRN", "JPN", "MEX", "SRB", "SWE", "THA", "USA", "ZAF")) |>
group_by(country, year) |>
summarise(stflife = mean(stflife,na.rm = T)) |>
ggplot(aes(x = year, y = stflife, color = country)) +
geom_line() +
geom_point()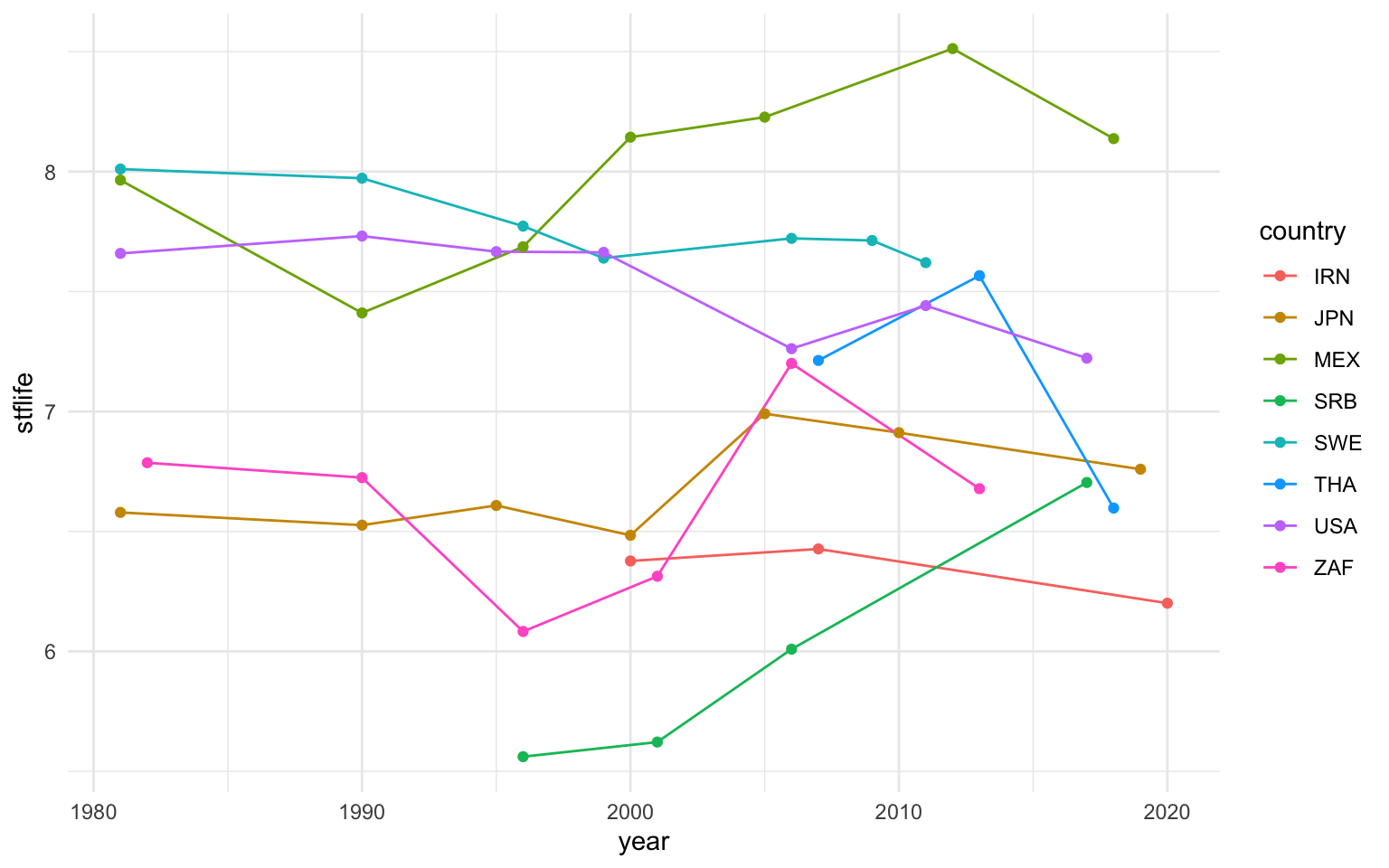
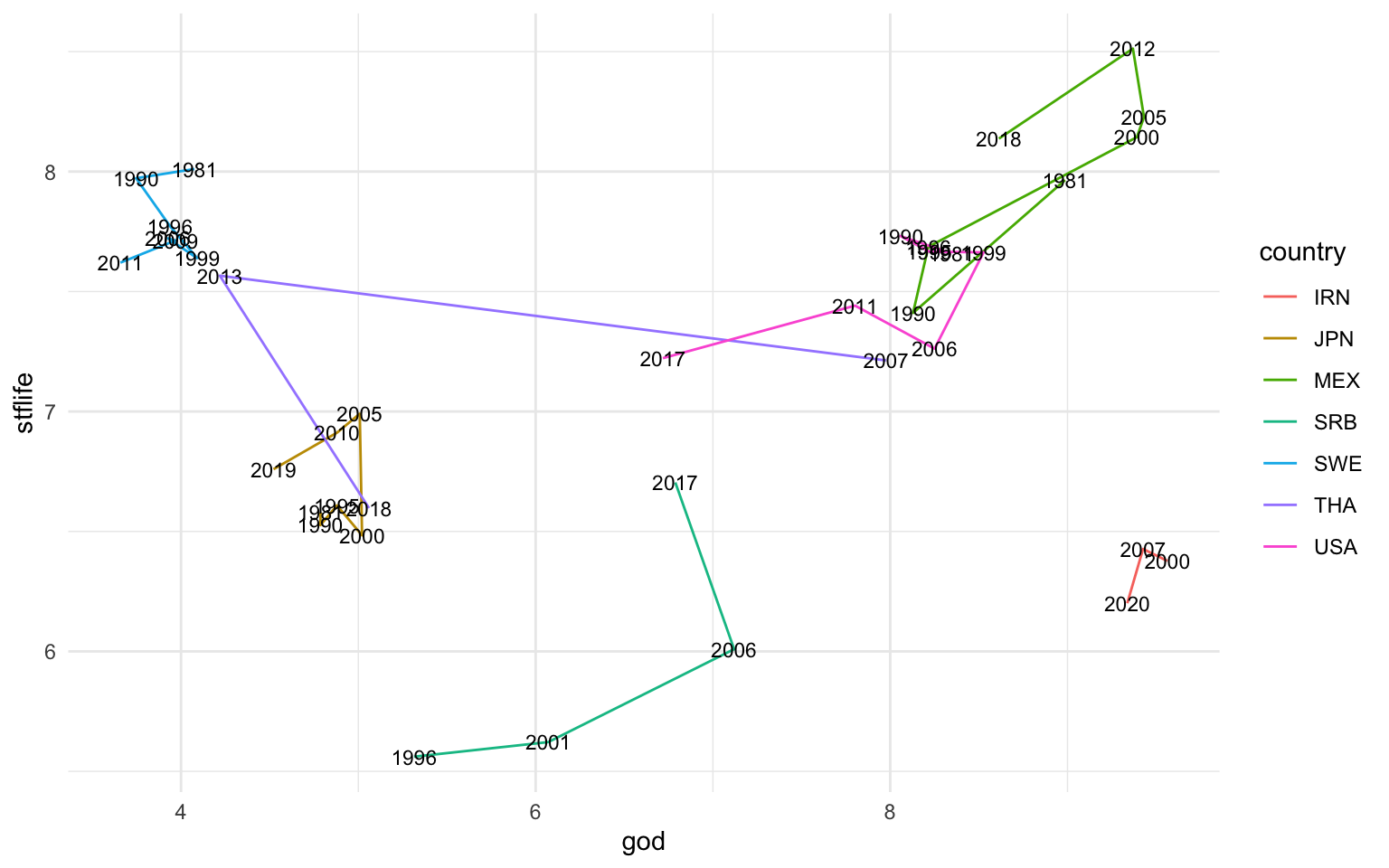
Hay otros tipos de gráficas que se utilizan con frecuencia para observar la evolución de una o diversas variables numéricas en el tiempo. En la figura 11.15 vemos dos ejemplos. En la gráfica de la izquierda observamos una línea LOESS2, que, como se explica en otro apartado, construye una línea suave para conectar varios puntos. En la gráfica de la derecha observamos lo que se denomina línea de trazado. Esta geometría (geom_path()) permite observar cómo dos variables numéricas evolucionan a lo largo del tiempo. Cada eje cartesiano representa una variable numérica y el color representa la línea temporal de una determinada observación. Podemos complementar esta línea de trazado con información textual de los años mediante geom_text().
2 Se explicarán sus características más adelante, en otro módulo.
Muestra el código
wvs |>
filter(country %in% c("IRN", "JPN", "MEX", "SRB", "SWE", "THA", "USA", "ZAF")) |>
group_by(country,year) |>
summarise(stflife = mean(stflife,na.rm = T)) |>
ggplot(aes(x = year, y = stflife, color = country)) +
geom_smooth(se = F)
wvs |>
filter(country %in% c('IRN','JPN', 'MEX', 'SRB', 'SWE', 'THA', 'USA')) |>
group_by(country, year) |>
summarise(stflife = mean(stflife,na.rm = T),
god = mean(god,na.rm = T)) |>
ggplot(aes(x = god, y = stflife)) +
geom_path(aes(col = country)) +
geom_text(aes(label = year), size = 3)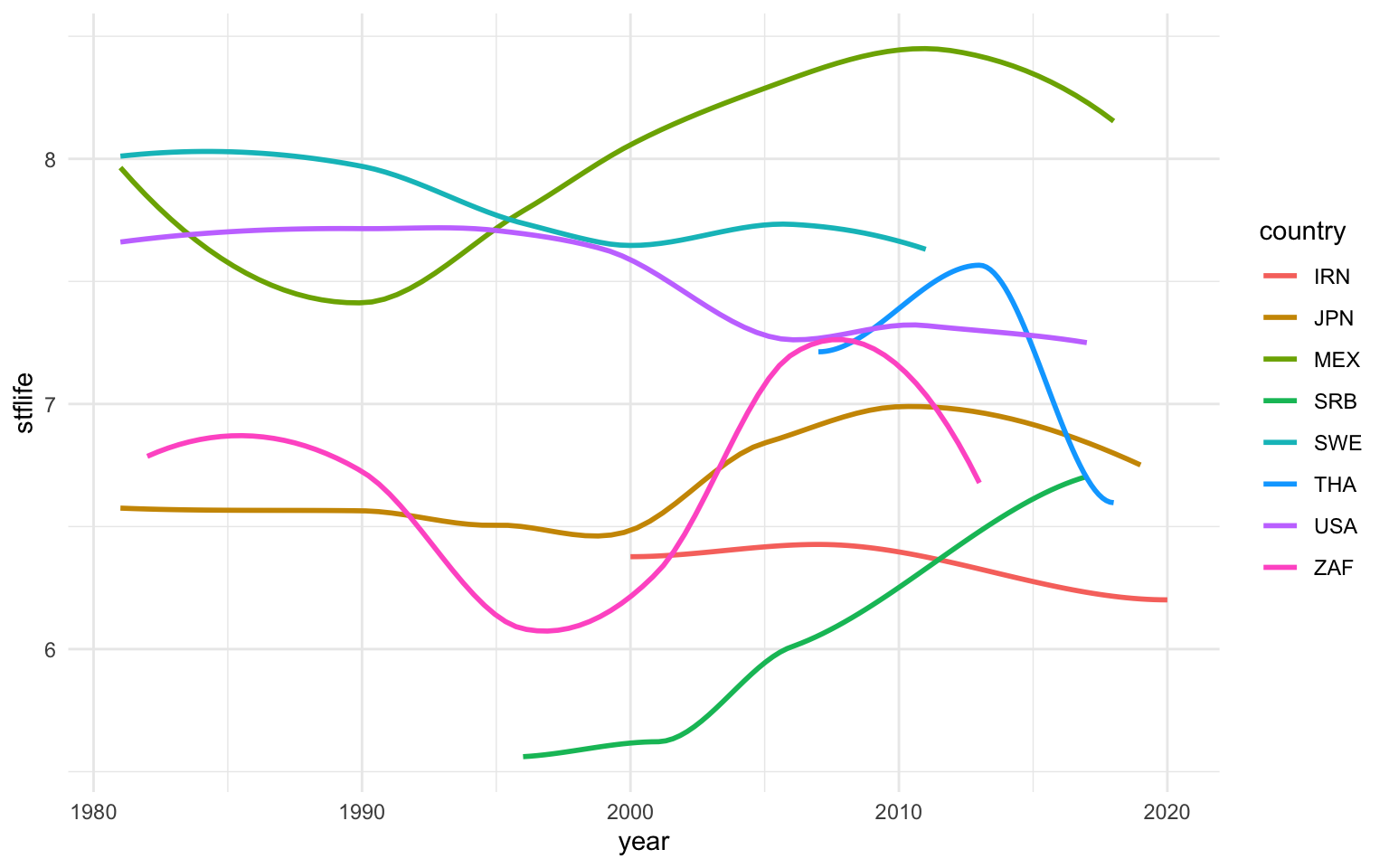
11.6 Dos variables numéricas
Finalmente, la manera más habitual de representar la relación entre dos variables numéricas es a partir de un diagrama de dispersión. Como se ha ido viendo en apartados anteriores, el diagrama de dispersión sitúa cada observación del marco de datos en un punto concreto fijado por dos esos cartesianos. La manera más habitual de representar un diagrama de dispersión es a partir de un diagrama de puntos. Así, si se quisiera saber si hay alguna relación entre la ubicación geográfica y el índice de innovación regional, se podría poner en relación la latitud de las regiones europeas con esta variable de innovación regional. En la figura 11.17 podemos ver un ejemplo:
La base de datos de las regiones europeas incluye información sobre la longitud y la latitud del centroide (un punto central del territorio de la región), hecho que permite geolocalizar de manera muy simple cada una de estas regiones. Así, si se genera un diagrama de puntos donde el eje de las \(x\) representa la longitud y el eje de las \(y\) la latitud, se podría reconstruir aproximadamente un mapa de Europa.
nuts |>
filter(lat > 20) |>
ggplot(aes(x = lon, y = lat)) +
geom_point()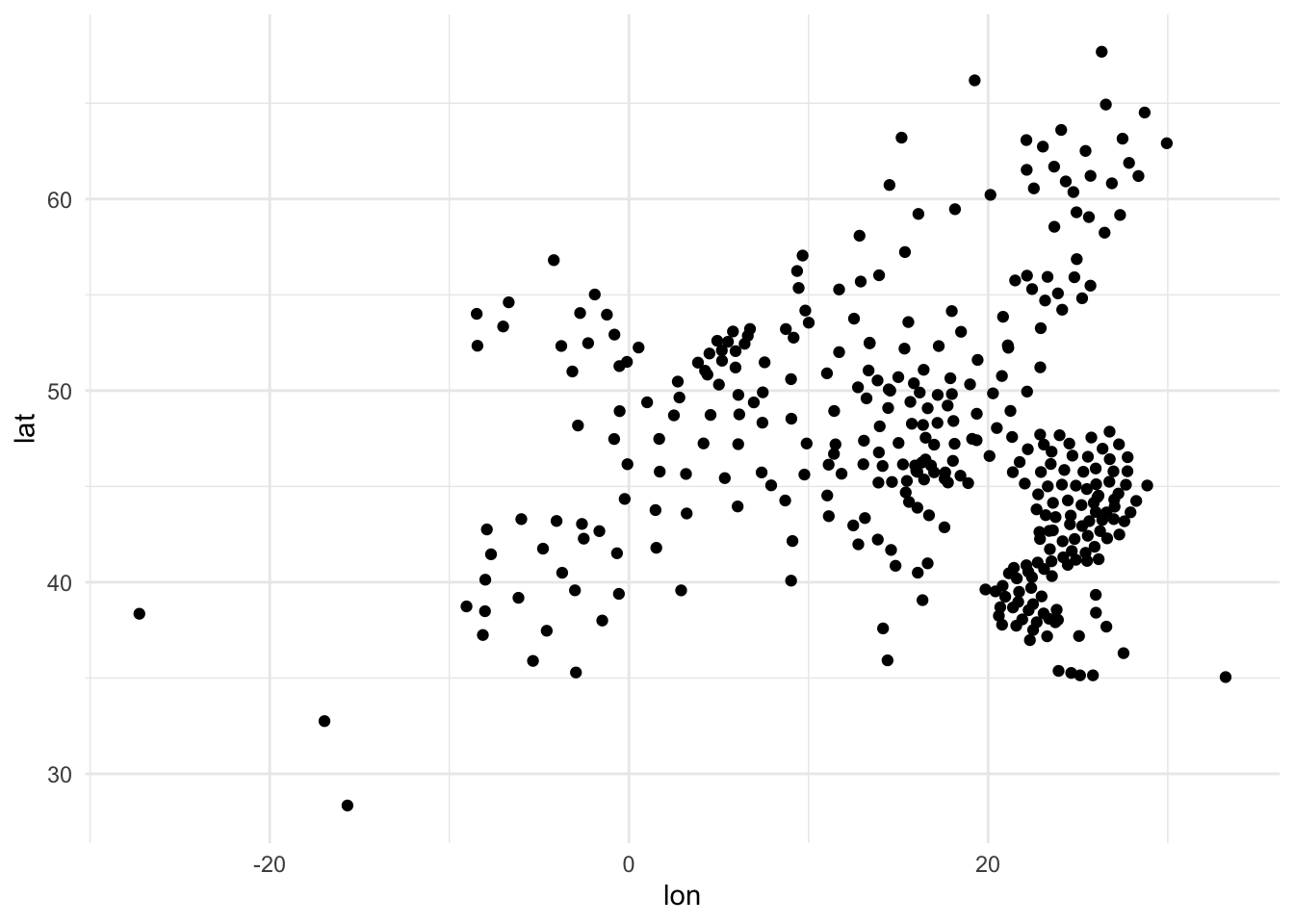
Ahora bien, uno de los principales elementos a tener en cuenta cuando se representan mapas es la escala y la proyección que se usa. A pesar de que no es un objetivo de esta sesión, R permite crear mapas de manera bastante simple con el paquete sf. Tenéis otro ejemplo al final del próximo apartado Otras capas. Para mayor información, se puede consultar esta web.
nuts |>
filter(lat > 20 & lon > -15) |>
ggplot(aes(x = innov, y = lat)) +
geom_point()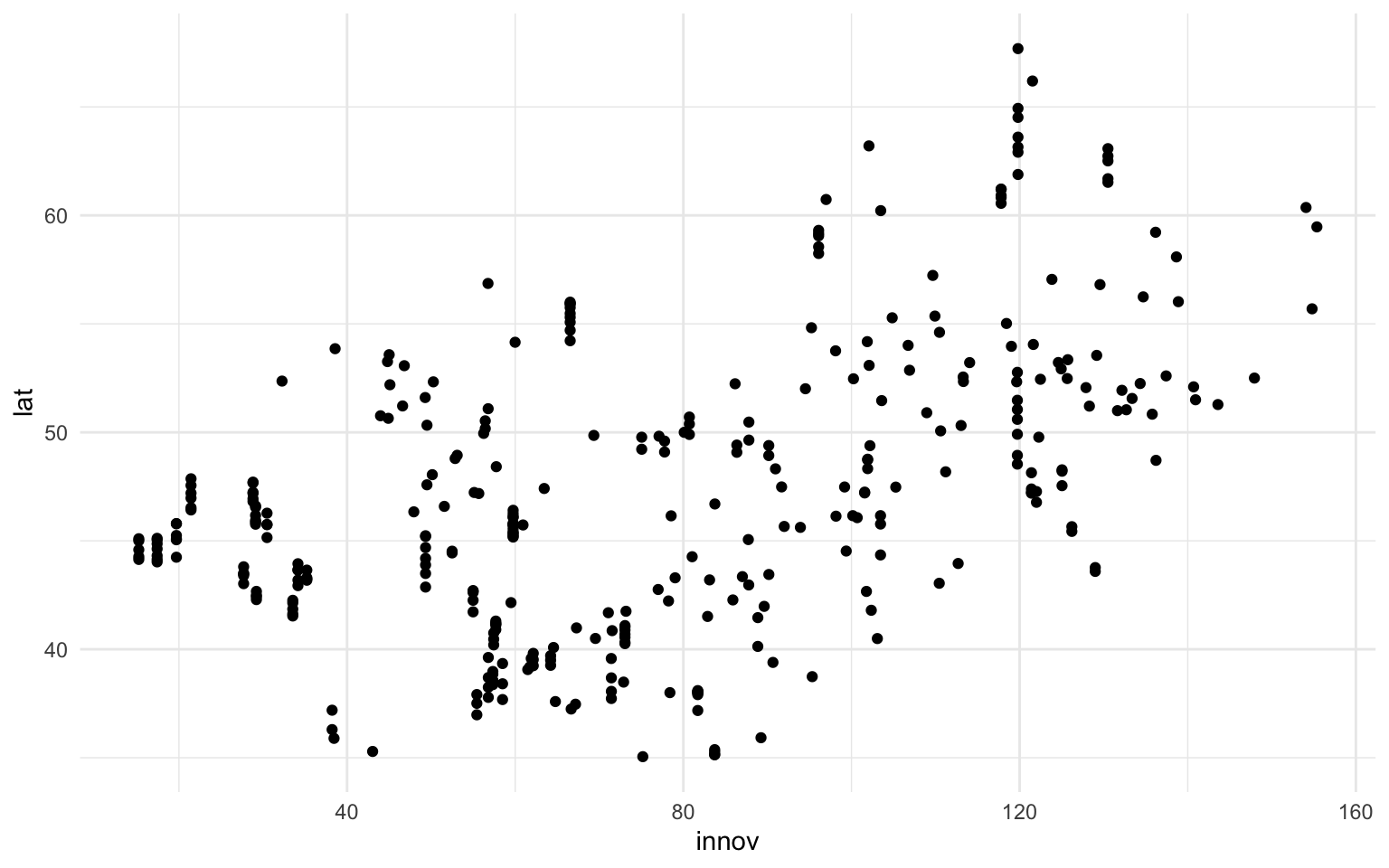
En el ejemplo anterior, para facilitar la legibilidad del diagrama, se han excluido las regiones europeas ultraperiféricas (regiones como Martinica o la Guayana francesa) y posteriormente se ha indicado al eje de las \(x\) la variable de innovación y al eje de las \(y\) la latitud. El diagrama resultante muestra una relación positiva entre estas dos variables y establece de manera descriptiva que las regiones más nórdicas de la Unión Europea son también las que tienen unos índices de innovación más elevados.
Como se ha visto en apartados anteriores, los puntos para representar las regiones no tienen que ser necesariamente puntos. El argumento shape de la función geom_point permite modificar la forma de estos puntos; también se podrían cambiar los colores, ya sea para todas las observaciones o a partir de terceras variables. Otra opción es indicar los puntos no con ninguna forma geométrica sino con el texto correspondiente a una de las variables del marco de datos. Esta opción, que se ejecuta con la función geom_text(),3 generalmente se asocia a la variable que identifica cada una de las observaciones de manera única. Para ejemplificarlo, la figura 11.18 replica la gráfica anterior pero sustituye la capa de puntos por la capa de texto.
3 La función geom_label() funciona de manera equivalente, pero añade un rectángulo detrás del texto para facilitar la lectura.
nuts |>
filter(lat > 20 & lon > -15) |>
ggplot(aes(x = innov, y = lat, label = nuts)) +
geom_text(size = 2)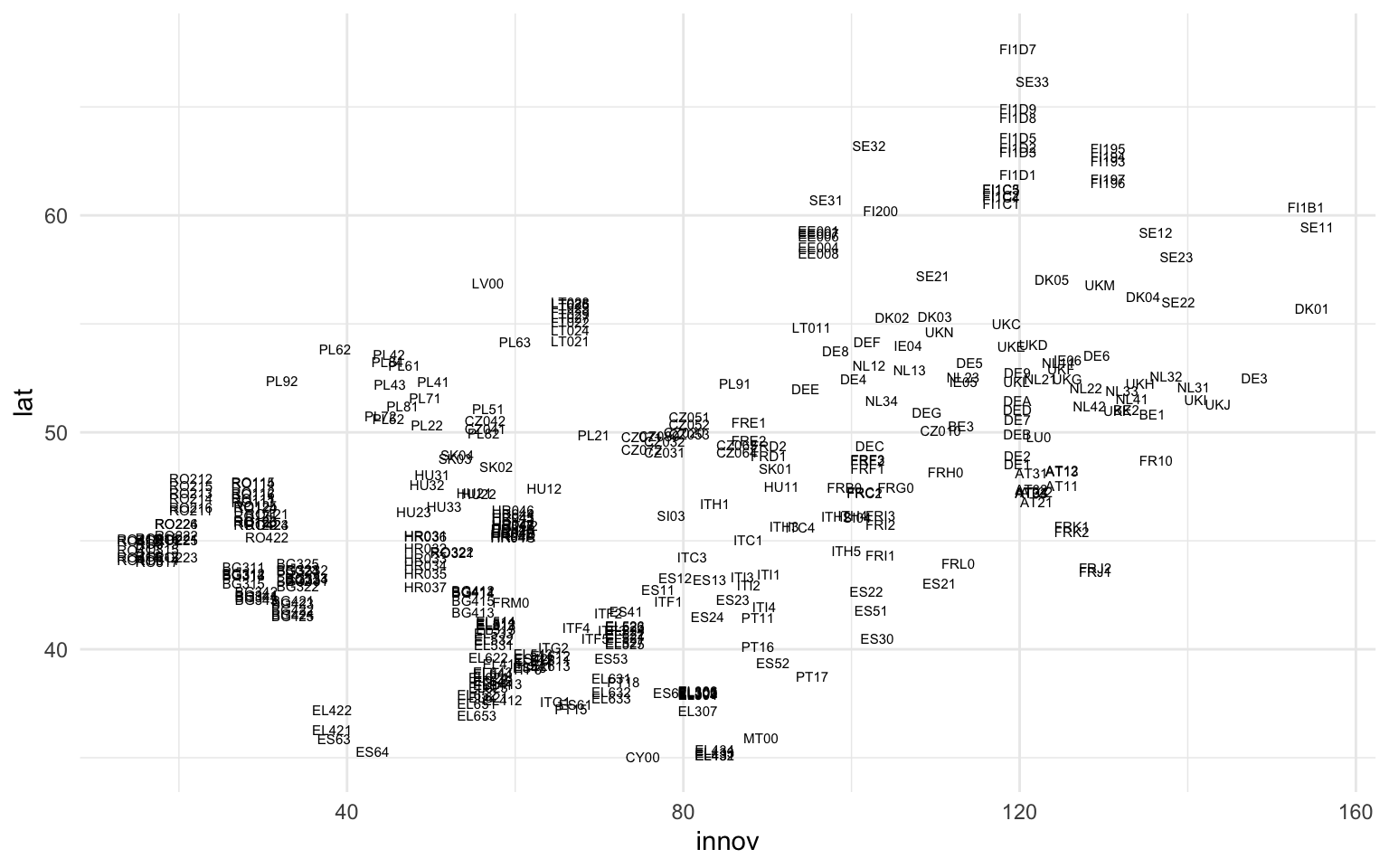
En la gráfica anterior cada una de las observaciones se sitúa, igual que en un diagrama de puntos, en el espacio cartesiano que sintetiza la posición en cada una de las dos variables. La gran diferencia es que, en lugar de puntos idénticos para todas las observaciones, cada observación está caracterizada por el código NUTS que identifica de manera única cada región europea. El elevado número de observaciones y la ubicación próxima al mapa pueden hacer que algunas sean más difíciles de leer, y por eso en estos casos puede ser necesario modificar el tamaño del texto con el argumento size.
Otra función interesante cuando se trabaja con dos variables numéricas es la función geom_jitter(). Esta función simplemente desplaza ligeramente cada punto respecto a la ubicación original de los ejes cartesianos.4 A pesar de que cuando se ponen en relación dos variables numéricas interesa saber en qué punto se sitúa cada observación respecto a cada una de las variables, cuando estas variables numéricas no son continuas sino discretas (por ejemplo, cuando hay escalas de 0 a 10), la acumulación de puntos en la misma ubicación puede enmascarar la cantidad de veces que ocurre esa coincidencia de valores. Situar los puntos de manera ligeramente dispersa puede ayudar a percibir de forma más fidedigna dónde se concentran la mayoría de los casos. Por ejemplo, la figura 11.19 muestra, con datos de la World Values Survey, cuál es la relación entre la ideología política y la creencia en Dios. Como ambas variables están creadas a partir de una escala de 1 a 10, todas las observaciones que coincidan en los mismos valores se sobrepondrán las unas a las otras.
4 Es una versión abreviada de la implementación de geom_point(position="jitter").
Muestra el código
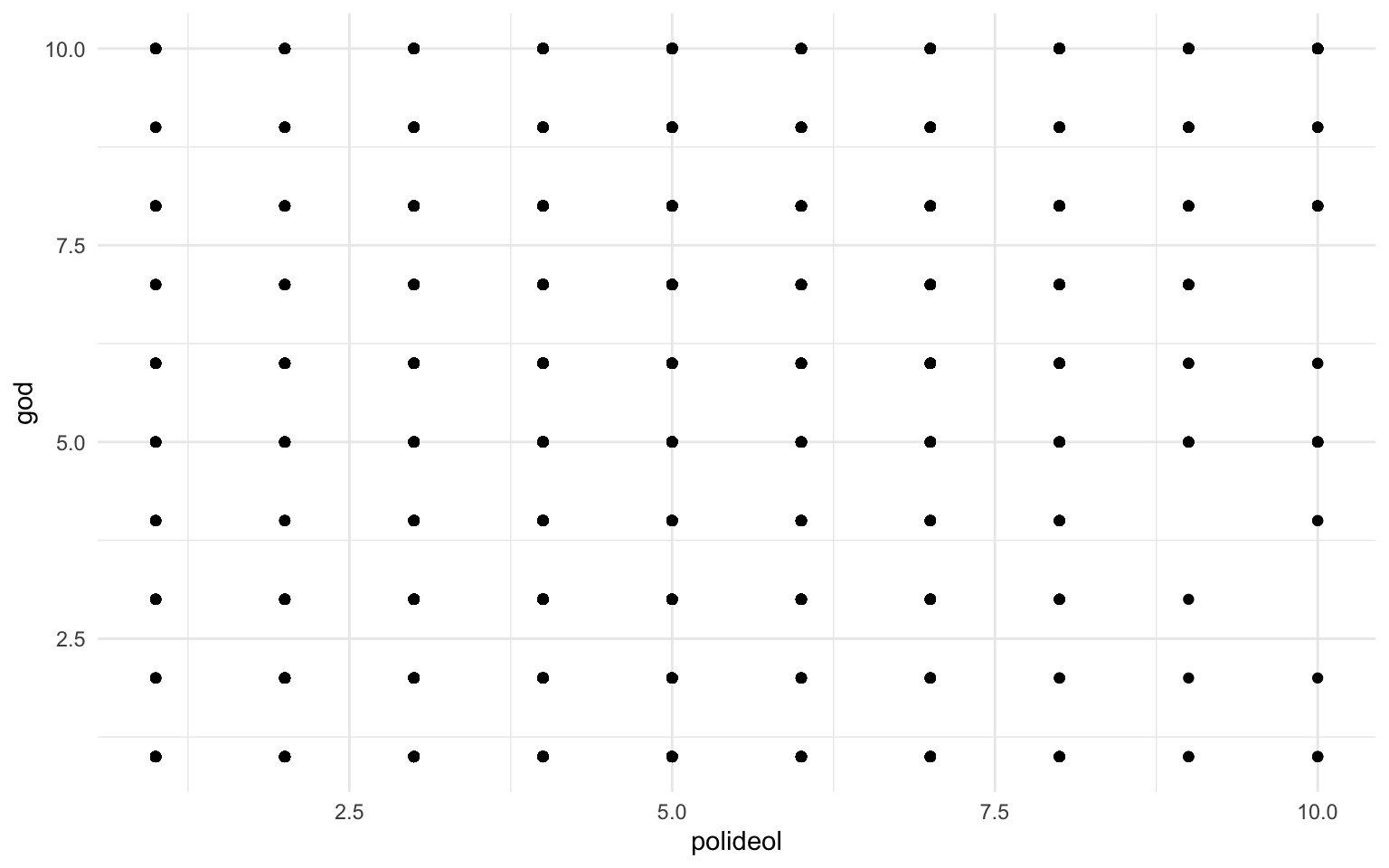

En la gráfica anterior, que se ha generado solo con los datos de España para facilitar la legibilidad, se puede ver que, cuando se usa la geometría geom_point(), es bastante complicado detectar algún patrón de relación entre ambas variables. Ahora bien, cuando se usa la geometría de puntos agitada (jitter), se puede ver con más facilidad en qué valores de cada una de las variables se concentra un número más elevado de observaciones. De este modo, es más fácil de interpretar y, más allá de la elevada concentración de individuos que se sitúan en el valor central de ideología (5), se puede apreciar que entre los individuos con valores menores de ideología la fe religiosa tiene valores más bajos y aumenta a medida que los individuos se definen con una ideología más derechista. Así, la geometría geom_jitter() ayuda a representar de manera más adecuada qué es la relación entre dos variables cuantitativas pero de tipo discreto.