10 El paquete ggplot2

10.1 Introducción

Toda la lógica de ggplot2 se construye de acuerdo con la “gramática de gráficas”, creada por Leland Wilkinson (2005) y que concibe cualquier gráfica como una estructura de diferentes capas. En cada capa añadimos un conjunto de elementos que responden a una finalidad concreta, de forma que permite organizar la construcción de la gráfica en diferentes fases. La gran ventaja del paquete ggplot2 es que permite aplicar siempre una misma estructura y seguir una misma lógica para crear las gráficas, independientemente del tipo de gráfica que se quiera visualizar. Cualquier gráfica ggplot2 tiene dos características principales:

La estructura está articulada a partir de la función ggplot()¹.
Necesita que se indiquen como mínimo las tres primeras capas (datos, proyección estética y geometría), mientras que las otras dos siempre serán opcionales aunque recomendables.

¹ Es necesario no confundir la función ggplot() (sin el número) del paquete ggplot2. Es en esta función donde se definen las dos primeras capas de la gráfica.

Ejercicio 10.1 (Preparación de los datos) Para seguir este módulo, necesitarás tener cargados varios paquetes de R. La mayoría (dplyr, ggplot2, etc.) están englobados en el paquete tidyverse (Wickham, 2023), y por tanto cargaremos directamente este paquete y eso ya cargará automáticamente todos los demás. También trabajaremos con tres bases de datos diferentes: Gapminder (Bryan, 2017), una versión de la World Values Survey (Inglehart et al., 2020) y un marco de datos de NUTS europeos (Sanjaume-Calvet et al., n.d.), que contiene datos de Eurostat, European Social Survey y European Quality of Government Dataset.

library(tidyverse)
library(gapminder)
nuts <- read_rds("nuts.rds")
wvs <- read_rds("wvs.rds")

Para ver mejor los ejemplos de este módulo, te recomendamos que cambies el tema que tienes por defecto en R. Podrás visualizar las gráficas con el tema theme_classic() si introduces el código siguiente en la consola:

theme_set(theme_classic())

¿Y cuáles son las capas de ggplot2 mínimas necesarias? A continuación, se indica la finalidad concreta que tiene cada una de las tres primeras capas, con el resultado visual que se consigue en el margen de la derecha:

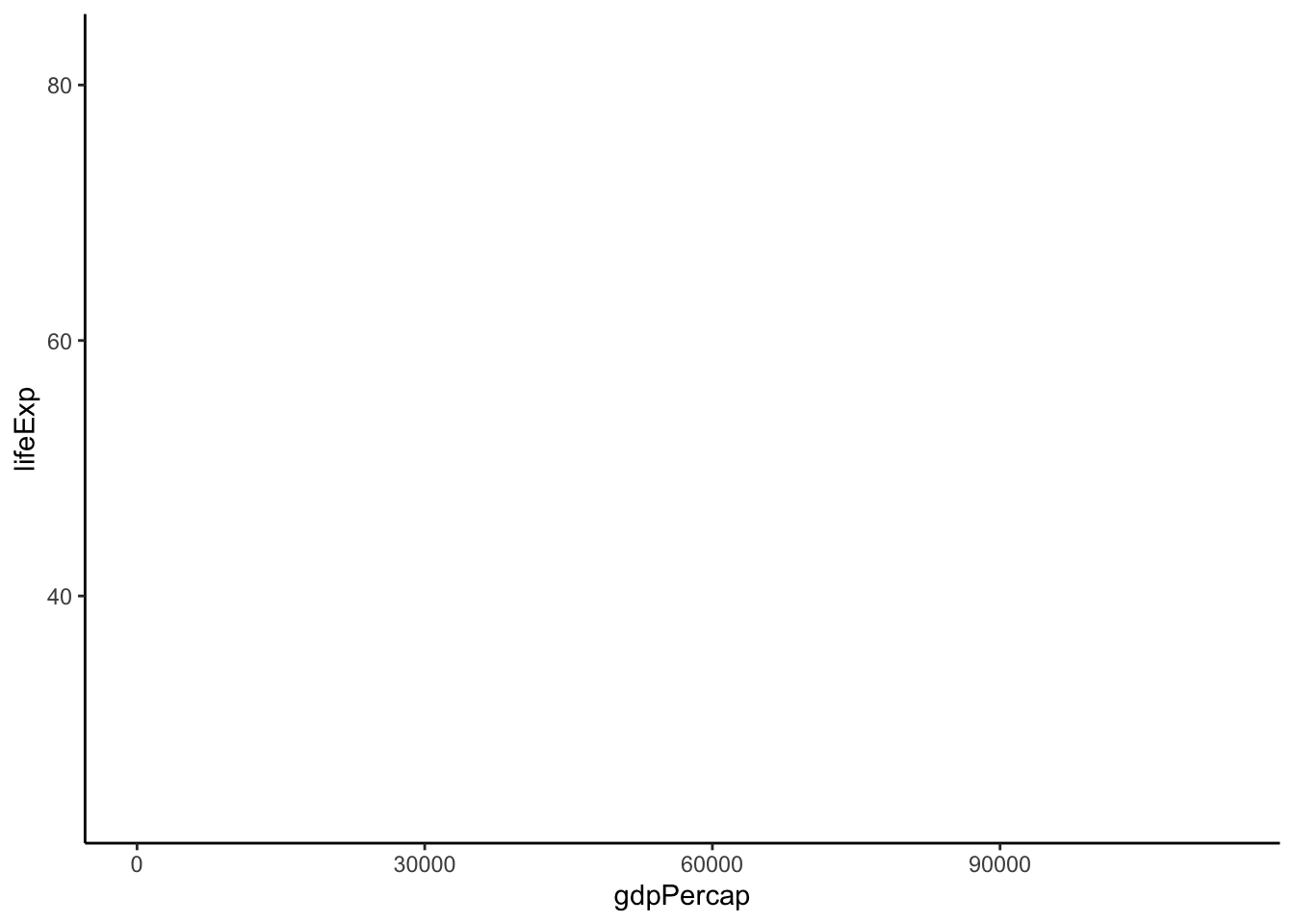
¿Qué información? En la primera capa ubicamos los datos a partir de los que se construirá la gráfica. Si activamos la función ggplot() y en el primer argumento indicamos el nombre de un marco de datos, R entenderá que tiene que reproducir una gráfica con estos datos. Por defecto, se reproduce un plot con coordenadas cartesianas, que consiste en un eje horizontal (también denominado de las \(x\)) y un eje vertical (también denominado de las \(y\)) (figura 10.1). La gráfica aparece en blanco porque R necesita indicar más información para poder reproducir una gráfica.

gapminder |> 
  ggplot()

gapminder |> 
  ggplot(aes(x = gdpPercap, 
             y = lifeExp))

gapminder |> 
  ggplot(aes(x = gdpPercap,
             y = lifeExp)) +
  geom_point()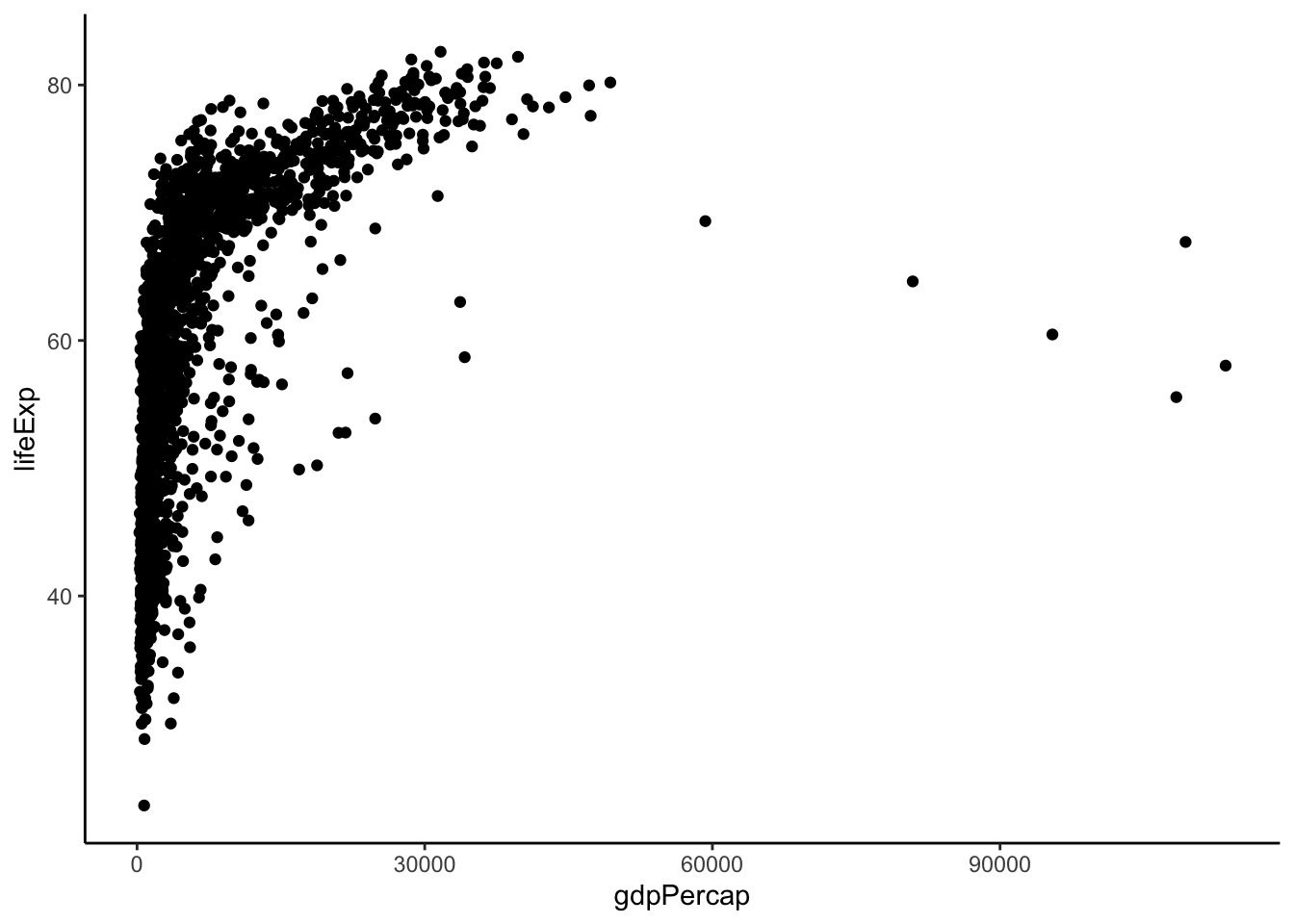

¿Qué se quiere comunicar? La segunda capa hace referencia a la proyección estética, en otras palabras, cuál o cuáles son las variables concretas que se usarán —y, si se trata de más de una variable, cómo se relacionarán entre ellas—. Dentro de la función aes() indicaremos que queremos usar las variables gdpPercap, que situaremos en el eje de las \(x\), y lifeExp, que situaremos en el eje de las \(y\) (figura 10.2). Fijaos como los ejes cambian e incluyen información sobre la variable. Cuando indicamos qué variable va en el eje de las \(x\), R nos prepara el eje horizontal con los datos de la variable en cuestión. El rango aproximado de la variable gdpPercap es de un mínimo de 241 y un máximo de 113.523 dólares per cápita. Con esta información, R crea un eje con unos límites que permitan introducir todos los datos de la variable. Como vemos, los límites del eje son 0 y 120.000.

El mismo procedimiento se seguirá cuando indicamos la variable que queremos poner en el eje de las \(y\). R buscará el rango de lifeExp (edad mínima de 23 y máxima de 82) y creará los límites del eje de acuerdo con estas coordenadas (mínimo de 20 y máximo de 85). Aunque tengamos información sobre ambos ejes, R todavía no sabe qué geometría tiene que utilizar para conectar los datos, de forma que dejará la inferior de la gráfica en blanco.

Sin embargo, todavía no vemos la gráfica porque nos falta indicar cómo queremos representar esta relación.

¿Cómo se quiere representar? La tercera capa representa el grupo de funciones en que se definen las geometrías (barras, puntos, líneas, etc.) que representarán la variable o las variables seleccionadas. Esta capa se indica fuera de la función ggplot() y se relaciona con esta función a partir del signo +². En este caso, hemos indicado con la función geom_point() que los puntos serán el elemento que conectará la información de las variables gdpPercap y lifeExp.

² En este bloque se tiene que usar la familia de funciones geom_...() que se verá más a fondo en la sección Tipos de visualizaciones

Aparte de las tres capas que acabamos de ver, hay otras capas que conforman los elementos contextuales, no esenciales pero necesarios en una buena gráfica, como son las coordenadas, escalas, títulos, etiquetas, diseños y otros elementos de contexto. Como la geometría, estas funciones tendrán que ir unidas a las anteriores con el símbolo +.

Coordenadas y escalas. Dan la información contextual para poder interpretar adecuadamente la representación gráfica.
Etiquetas y títulos. Dan un contexto interpretativo para facilitar la comprensión de la gráfica.

Para aprovechar al máximo la potencia de ggplot2, hay que acostumbrarse a elaborar las gráficas pensando no solo qué tipo de gráfica se quiere hacer, sino también cuáles son todos los elementos que se quiere que aparezcan en la gráfica. Por eso la lógica de capas, asociada directamente con la estructura del código de ggplot2, es tan útil para generar gráficas efectivas. Como se ha dicho hasta ahora, todo empieza con la función ggplot() y a continuación se sigue el orden de bloques y capas³. El esqueleto básico y común de todas las gráficas creadas con ggplot2 tendría que ser el siguiente:

³ Es importante no confundir la lógica de las capas con diferentes funciones en R. Si bien la indicación de los datos y la proyección estética se hace (casi) siempre del mismo modo, hay funciones específicas para indicar los diferentes objetos geométricos y se pueden usar diferentes funciones para especificar una capa. Más adelante se verá cómo y por qué.

marco de datos |> 
   ggplot(aes(estéticos x, y, etc.)) +
   geometría +
   escalas +
   coordenadas +
   temas

En los epígrafes siguientes se presentará, paso a paso y con ejemplos, cuáles son los elementos necesarios para crear gráficas con ggplot2. Concretamente, en este capítulo se usará la base de datos de las regiones europeas, almacenadas en el objeto nuts.

Ideas principales de ggplot2

Es muy importante remarcar algunos aspectos fundamentales de ggplot2:

El paquete se llama ggplot2, pero la función para crear gráficas es ggplot() sin el ‘2’ final.
Dentro de los paréntesis de la función ggplot() situaremos dos capas: los datos y la proyección estética.
Las otras capas de la gráfica se unen mediante el símbolo +. Es importante que todas las capas que se añadan a la gráfica estén asociadas a la función ggplot() con este símbolo. En caso contrario, la gráfica no se generará de manera adecuada.

10.2 Marco de datos

Cualquier gráfica requiere unos datos que contengan la información que se quiere comunicar. La forma predefinida por la función ggplot() para especificar el marco de datos con el que se quiere trabajar es indicándolo a partir del argumento data. Es decir, para generar una gráfica con la base de datos nuts, se tendría que usar el código siguiente:

ggplot(data = nuts)

Ahora bien, cuando se ejecuta este código, la única consecuencia es que se genera una imagen vacía, en blanco (figura 10.4). Esto es porque solo indicando el origen de los datos no hay bastante para generar la gráfica. ggplot2 espera que se le indique también cuál es la información concreta que tendrá que graficar. Esto se hace a partir del segundo argumento de la función ggplot(), como se verá en el apartado siguiente.

Antes de esto, sin embargo, es importante remarcar dos aspectos sobre cómo se puede indicar el marco de datos que se usará en la gráfica. Por un lado, no es obligatorio indicar el argumento data =. Si simplemente se indica el nombre del objeto donde se almacena el marco de datos después del paréntesis, ggplot2 interpretará correctamente que ese es el objeto a partir del que tiene que extraer la información para la gráfica.

En segundo lugar, las funciones de ggplot2 se pueden enlazar con la lógica de pipes. Por lo tanto, tal como se ha mostrado en secciones anteriores, se puede poner el marco de datos al principio del código antes de indicar la función ggplot(). Esto permite, en caso de que sea necesario, hacer transformaciones del marco de datos con el paquete dplyr y a continuación enlazarlo con una pipe con la función ggplot(). Por ejemplo, si en lugar de trabajar con todas las regiones europeas solo se quisiera trabajar con las regiones francesas e italianas, se podría hacer de la forma siguiente:

nuts |> 
  filter(ccode %in% c("IT","FR")) |> 
  ggplot()

10.3 Proyección estética

Una vez ya se ha indicado el primer argumento de la función ggplot(), ya se puede empezar a graficar la información más específica que aparece en la base de datos indicada. El siguiente paso, la segunda capa de ggplot2, consiste en definir los estéticos: qué variables se quieren representar gráficamente. Esto se hace a partir de mapping, el segundo argumento de la función ggplot(). Este argumento siempre va seguido de la función aes(), que se encarga de definir la proyección estética (aes es una abreviación de aesthetics) e indicar cuál será el rol de cada una de las variables. A la hora de definir las proyecciones estéticas, siempre se tiene que definir una variable como mínimo, generalmente en el eje de las \(x\) y, por lo tanto, representada en el eje horizontal. En casos en que la gráfica tenga que representar relaciones entre dos variables, también se tendría que definir una variable en el eje \(y\), que quedará representado en el eje vertical.

Para introducir las gráficas con ggplot2, se empezará trabajando con un tipo de gráfica, conocida como diagrama de dispersión, que pone en relación dos variables. Las dos variables de la base de datos nuts que se usarán son el nivel de innovación de la región definido por la Comisión Europea, que se situará en el eje \(x\), y los niveles medios de satisfacción con el gobierno de acuerdo con los datos de la Encuesta Social Europea, en el eje \(y\). En ggplot2 se tendría que especificar la primera capa como se ha hecho antes, indicando el objeto donde está el marco de datos, y, posteriormente, en la función aes(), indicar qué variable se quiere representar en cada uno de los ejes. El resultado lo observamos en la figura 10.5:

nuts |> 
  ggplot(mapping = aes(x = innov, y = stfgov))

Figura 10.5: Segunda capa (proyección estética)

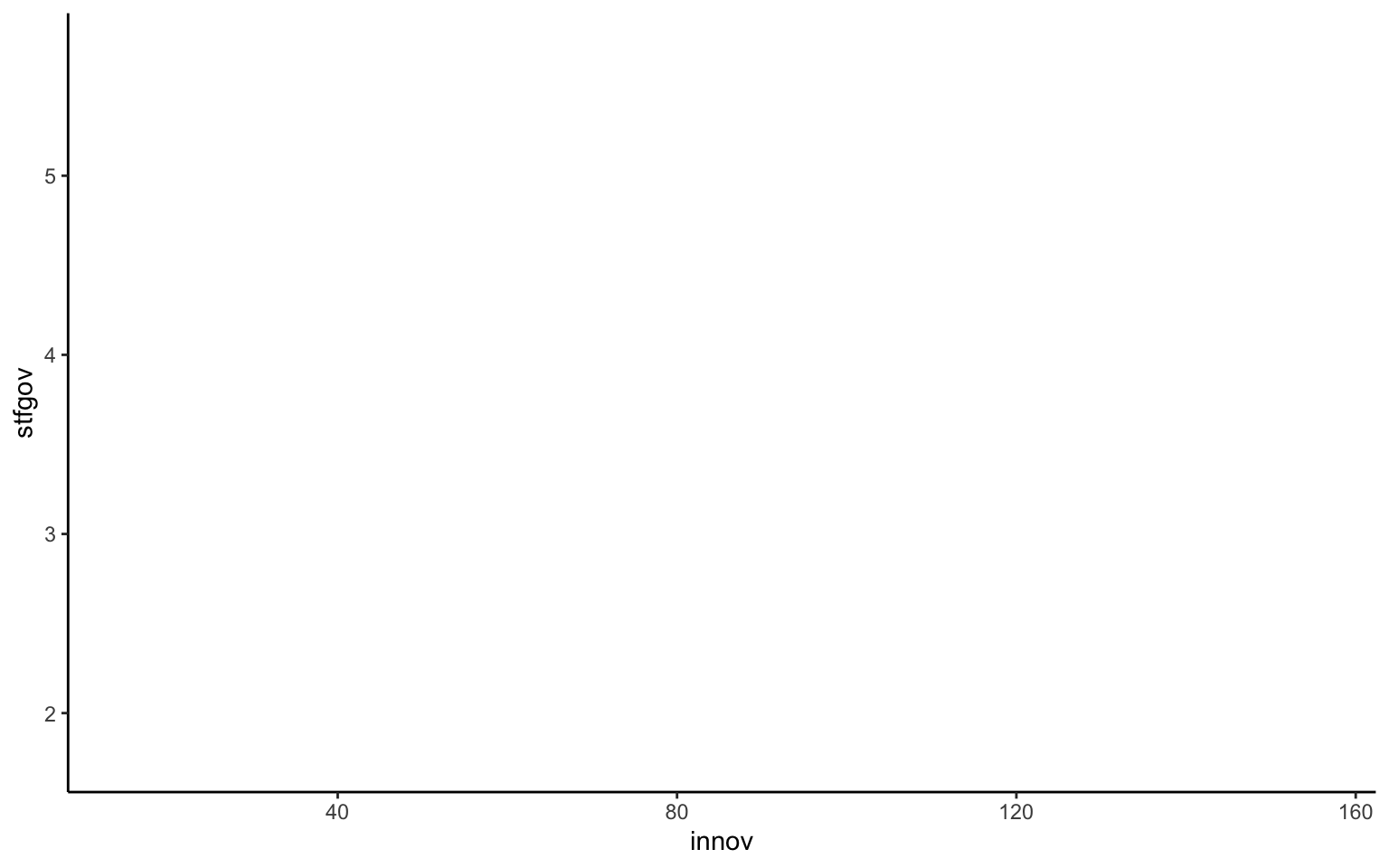
Es importante destacar que no ha habido ningún problema. ggplot() ha generado exactamente lo que se le ha pedido. A pesar de que es cierto que ahora la imagen ya no aparece completamente en blanco, ggplot2 sigue sin mostrar información en la gráfica. Solo con las dos capas definidas genera una gráfica vacía porque todavía no se le ha especificado cómo se quiere llenar la gráfica. Ahora bien, respecto a la anterior imagen que se generaba cuando solo se indicaba la capa referente a los datos, al menos en esta segunda capa ya se pueden observar las cuadrículas con los valores de las dos variables. Además, esto permite hacerse una idea de los valores que adoptarán los datos de los que se dispone en cada una de las variables. Ya se puede saber que la variable de innovación (eje \(x\)) tendrá un rango entre 20 y 160, y que la satisfacción con el gobierno (eje \(y\)) se moverá entre los valores 2 y 5.5.

A la hora de definir la proyección estética, también se pueden añadir otras variables en una gráfica. Por ejemplo, podría ser interesante observar si la relación entre las variables innovación y satisfacción con el gobierno difiere entre países. Esta variable categórica se podría añadir como proyección estética, ya sea modificando el color, la forma o el tamaño de los datos cuando se representen en la gráfica. En el apartado Distinguir entre estéticos y atributos se profundiza con más detalle sobre cómo se pueden hacer estos cambios.

Finalmente, igual como pasaba con la primera capa, es importante remarcar que en ggplot() no hay que indicar el argumento mapping para definir la proyección estética de la gráfica. Simplemente con indicar la función aes() dentro de la función ggplot() es suficiente.

10.4 Geometría

Para poder terminar la gráfica, hay que definir una tercera capa, la que completa los elementos mínimos para generar una gráfica con ggplot2. El único elemento que falta es indicar qué objeto geométrico se quiere usar para representar la variable o las variables seleccionadas. Aquí es importante recordar que esta tercera capa siempre se indica fuera de la función ggplot(), pero que se vincula a esta función a través del símbolo +. Otro elemento relevante es que es precisamente en la geometría que se acaba definiendo qué tipo de gráfica se genera y que cada tipología de gráfica tiene una función asociada. Todas las funciones empiezan con la partícula geom_, pero hay funciones diferenciadas según si se quiere crear, por ejemplo:

Un histograma: geom_histogram().
Un diagrama de cajas: geom_boxplot().
Una gráfica de barras: geom_bar().

Ejercicio 10.2 (¿Qué geometrías tenemos?) ¡El paquete ggplot2 tiene hasta 35 geometrías! Para hacerte una idea más visual de cuáles son estas geometrías, descarga el Cheat sheets de ggplot2. Este documento te será muy útil a lo largo de este módulo.

Para ver un resumen de todas las geometrías disponibles, ejecuta el código siguiente:

help.search("geom_", package = "ggplot2")

10.4.1 Tipos de geometrías

Siguiendo con el ejemplo anterior, para mostrar la relación entre dos variables numéricas como son los niveles de innovación regionales y la satisfacción con el gobierno, la gráfica más adecuada es el diagrama de dispersión. Por eso, en la geometría se especificará la función geom_point(). Esta geometría dibuja un punto para cada observación del marco de datos. La ubicación del punto en la gráfica depende de los valores de esta observación en las dos variables definidas en el eje de las \(x\) y las \(y\). De este modo, se puede saber, para el conjunto de datos, si las observaciones con valores más altos en una variable también tienen valores altos en la otra variable o no. El código para generar la gráfica final sería el siguiente:

nuts |> 
  ggplot(mapping = aes(x = innov, y = stfgov)) + 
  geom_point()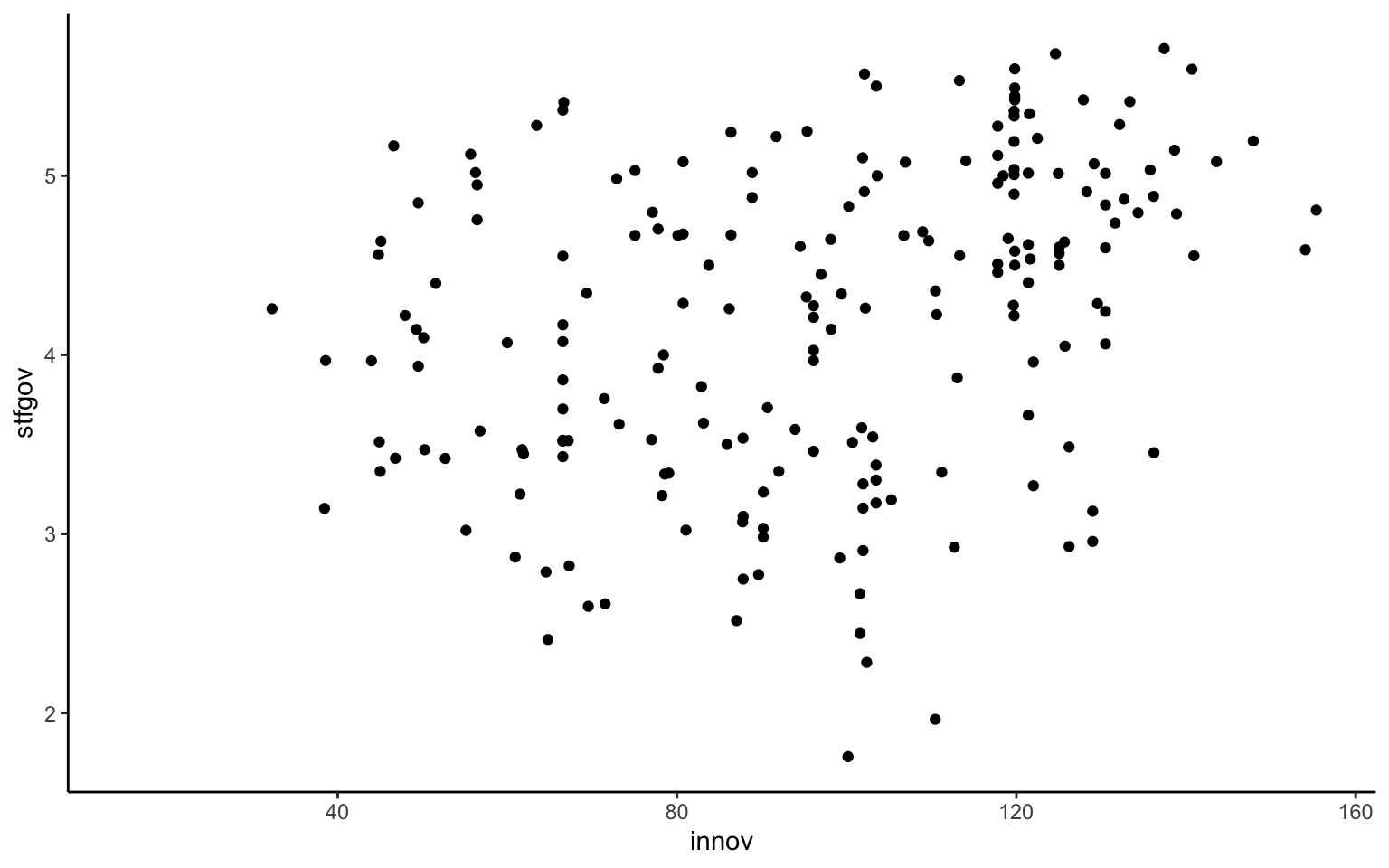

Figura 10.6: Tercera capa (geometría puntos)

Ahora sí que, usando ggplot2, se ha podido generar una gráfica (figura 10.6) con toda la información básica. A partir de la base de datos nuts, se han seleccionado las dos variables de interés (nivel de innovación y satisfacción con el gobierno) y se ha generado una gráfica, un diagrama de dispersión, que representa la relación entre ambas variables. En esta gráfica, cada punto representa una región europea y la ubicación de cada punto en el área viene determinada por el valor que adopta cada región tanto en cuanto a niveles de innovación como de satisfacción con el gobierno.

Una manera alternativa de representar esta relación entre estas dos variables podría ser estimando la relación lineal entre ellas. En este caso, algunos de los elementos básicos ya están definidos, el origen de los datos es el mismo y las dos variables ya han sido definidas en la proyección estética. El único que habría que cambiar es la geometría, es decir, la forma como se representa la relación entre las variables. La geometría que se tendría que usar, en este caso para mostrar una relación lineal entre variables, es geom_smooth(). Puesto que lo que se quiere es que la relación entre las dos variables sea lineal simple (una recta con una única pendiente), se tiene que especificar el argumento method = "lm" dentro de la función. El resultado es el siguiente:

nuts |> 
  ggplot(mapping = aes(x = innov, y = stfgov)) + 
  geom_smooth(method = "lm")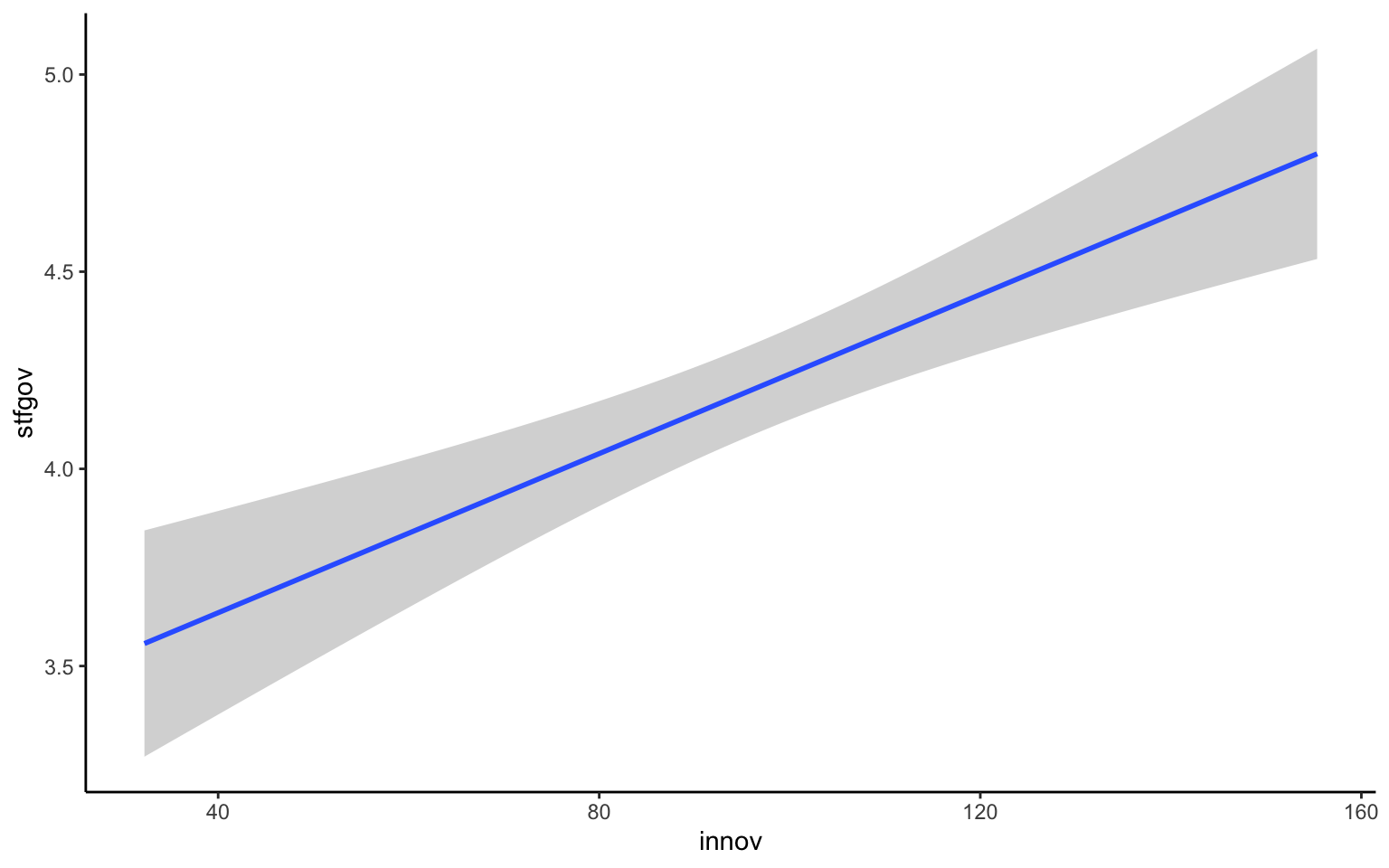

Figura 10.7: Tercera capa (geometría línea)

En la figura 10.7 parece que hay una relación positiva entre estas dos variables, puesto que la línea tiene una pendiente ascendente. Este ejemplo nos muestra que, simplemente cambiando la función de la geometría, se puede obtener una gráfica diferente, pero que sigue con la misma lógica de implementación de ggplot2. Lo único que cambia es que la forma de representar la relación entre ambas variables usa una geometría diferente: en lugar de usar puntos para mostrar cada una de las observaciones, la relación se muestra a partir de una línea, que ajusta de manera más adecuada la relación entre ambas variables.

Tal como se ha dicho antes, hay tres capas mínimas para poder generar una gráfica, pero a partir de aquí se pueden ir sobreponiendo diferentes capas en una gráfica. Estas capas no tienen que ser necesariamente de elementos diferentes. De hecho, es posible combinar en una única gráfica diferentes representaciones geométricas de una misma relación. Para poner un ejemplo, si se quisiera comparar la representación geométrica en puntos y la representación de la línea que relaciona innovación y satisfacción con el gobierno, se podría pedir una gráfica que combinara ambas representaciones geométricas. El resultado sería el siguiente:

nuts |> 
  ggplot(mapping = aes(x = innov, y = stfgov)) + 
  geom_point() +
  geom_smooth(method = "lm")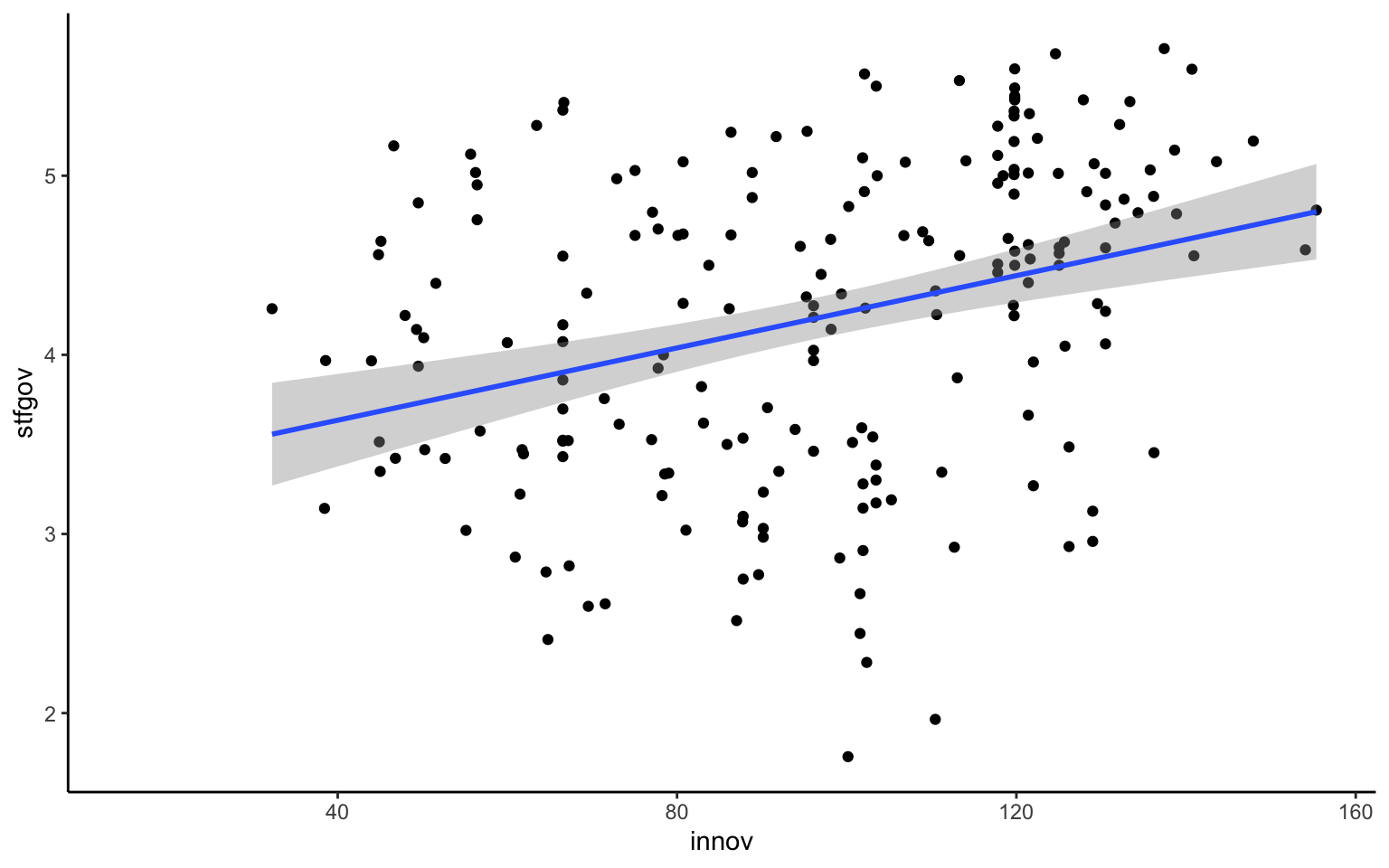

Figura 10.8: Tercera capa (múltiples geometrías)

El orden de las capas

Un elemento importante cuando se añaden diferentes geometrías en una única gráfica es que el orden de las capas es relevante, puesto que se sobrepondrán las unas a las otras. Si se quiere que los puntos queden detrás de la imagen, es importante definir primero la geometría de puntos y después la de línea. En este caso, la orden sí que puede alterar el producto final.

A partir de sobreponer dos capas de geometría, se pueden comparar diferentes formas de poner en relación estas dos variables. Así, a pesar de que la línea de la figura 10.8 nos muestra una relación positiva entre las variables (cuanta más innovación más satisfacción con el gobierno), los puntos muestran que esta relación no es tan directa como parece mostrar la recta. Técnicamente, se diría que los datos están muy dispersos porque una buena parte de los puntos se alejan de la trayectoria de la recta.

Más adelante, en el apartado Tipos de visualizaciones se presentarán en detalle algunas de las geometrías de uso más habitual. A modo de síntesis, la lista siguiente muestra una relación de las diferentes gráficas y geometrías posibles y la función asociada para generarlas.

Diagrama de barras geom_bar(): pensado para representar variables de tipo categórico o cualitativo.
Histograma geom_histogram(): pensado para representar la distribución de valores de una variable cuantitativa continua.
Diagrama de densidad geom_density(): similar al histograma.
Diagrama de caja geom_boxplot(): pensado para representar la distribución de valores, es valioso para comparar las distribuciones a partir de una segunda variable categórica.
Diagrama de líneas geom_line(): pensado para mostrar la evolución de una variable a partir de una segunda variable, generalmente de tipo temporal.

10.4.2 Atributos

En los ejemplos anteriores, a la hora de añadir las geometrías se ha confiado en las consideraciones estéticas predefinidas por el paquete ggplot2. Todas las geometrías están asociadas a unas características o atributos por defecto. Por ejemplo, se ha visto que los puntos añadidos con geom_point() son completamente negros, tanto por dentro como en los bordes, y con un tamaño predeterminado. ggplot2 está diseñado para generar gráficas simples para facilitar la comprensión, y, por lo tanto, generalmente no habrá que modificar las características predefinidas. Ahora bien, a veces puede ser necesario modificar algunos de estos atributos para ajustarse a los requisitos de la publicación que se quiere hacer o para comunicar de manera más efectiva —se puede pensar en un caso en el que ciertas categorías están generalmente asociadas con un color concreto, habría que forzar R a colorear aquellas categorías de acuerdo con la norma social—. Los cambios en los atributos de las geometrías se tienen que indicar siempre dentro de la función de la geometría, puesto que, como se ha visto, si se deja el paréntesis vacío se implementan las opciones por defecto.

De entre los diferentes atributos, hay algunos que son comunes a todas, o prácticamente todas, las geometrías. Los más frecuentes son color, fill, size y alpha. A continuación, se exponen algunas de sus especificidades.

Tanto color como fill sirven para especificar el color de la geometría. Se diferencian porque hay algunas geometrías donde se puede distinguir entre el borde y el relleno; en estos casos, color hace referencia al borde y fill al relleno. Ambos atributos, color y fill, se pueden definir de tres formas diferentes:

Por un lado, se puede escribir el nombre del color simplemente indicando, por ejemplo, color = "red"; R dispone de 657 colores diferentes que se pueden consultar ejecutando la función colores().
La segunda forma, que permite especificar cualquier color posible, es indicando entre comillas el código hexadecimal rgb del color que se quiere definir. Este código hexadecimal tiene que seguir el formato color = "#RRGGBB", en el que cada par de valores (RR, GG, BB) consiste en dos dígitos hexadecimales en el rango entre 00 y FF.
Si lo que se quiere es que el color sea absolutamente transparente, se tiene que indicar como color = NA.

Dónde se pueden encontrar colores

Se pueden denominar los colores de centenares de maneras diferentes. En esta web se muestran los colores y sus nombres asociados. En esta web encontraréis una herramienta para definir el código hexadecimal para cualquier color.

Manipulando los atributos, se puede modificar cualquier gráfica. Siguiendo con el ejemplo anterior de la relación entre innovación y satisfacción con el gobierno, si se quisiera generar una gráfica en blanco y negro —a menudo esto nos puede interesar para ahorrar tinta y facilitar la publicación de gráficas—, se podría cambiar el color tanto de los puntos como de la línea. Así, se podría generar el diagrama de dispersión con puntos grises y una línea de tendencia de color negro. Además, nos interesa que el área colorida alrededor de la línea tenga un color gris más claro. Para conseguir estos cambios (figura 10.9), se podrían definir los atributos de la forma siguiente:

nuts |> 
  ggplot(mapping = aes(x = innov, y = stfgov)) + 
  geom_point(color = "gray") +
  geom_smooth(method = "lm", color = "black",fill = "lightgray")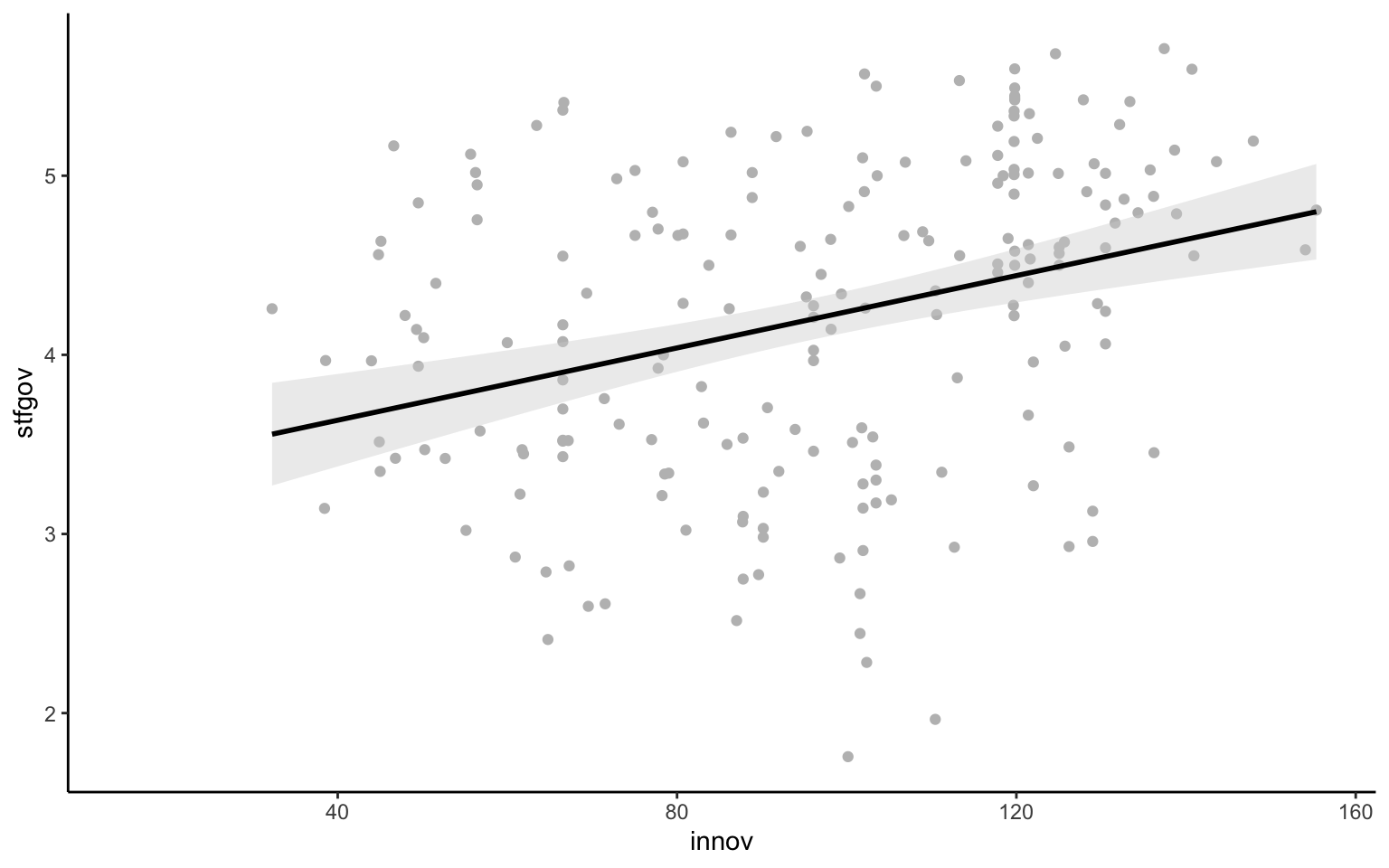

Figura 10.9: Definición de atributos, color y fill

Una vez hechos estos cambios, quizás sería interesante modificar el tamaño de los puntos para que pasen más desapercibidos en la gráfica. Otro atributo genérico que se puede utilizar en una gran parte de las geometrías es size, que permite controlar el tamaño de la geometría en cuestión. Por defecto, tiene el valor 1.5. Si se quiere modificar, es importante tener en cuenta que, cuando se indican valores más elevados, el tamaño de la geometría aumentará, y con valores más bajos será más pequeña. En este caso, para obtener puntos más pequeños se podría definir con el valor 1 (figura 10.10).

nuts |> 
  ggplot(mapping = aes(x = innov, y = stfgov)) + 
  geom_point(color = "gray", size = 1) +
  geom_smooth(method = "lm", color = "black", fill = "lightgray")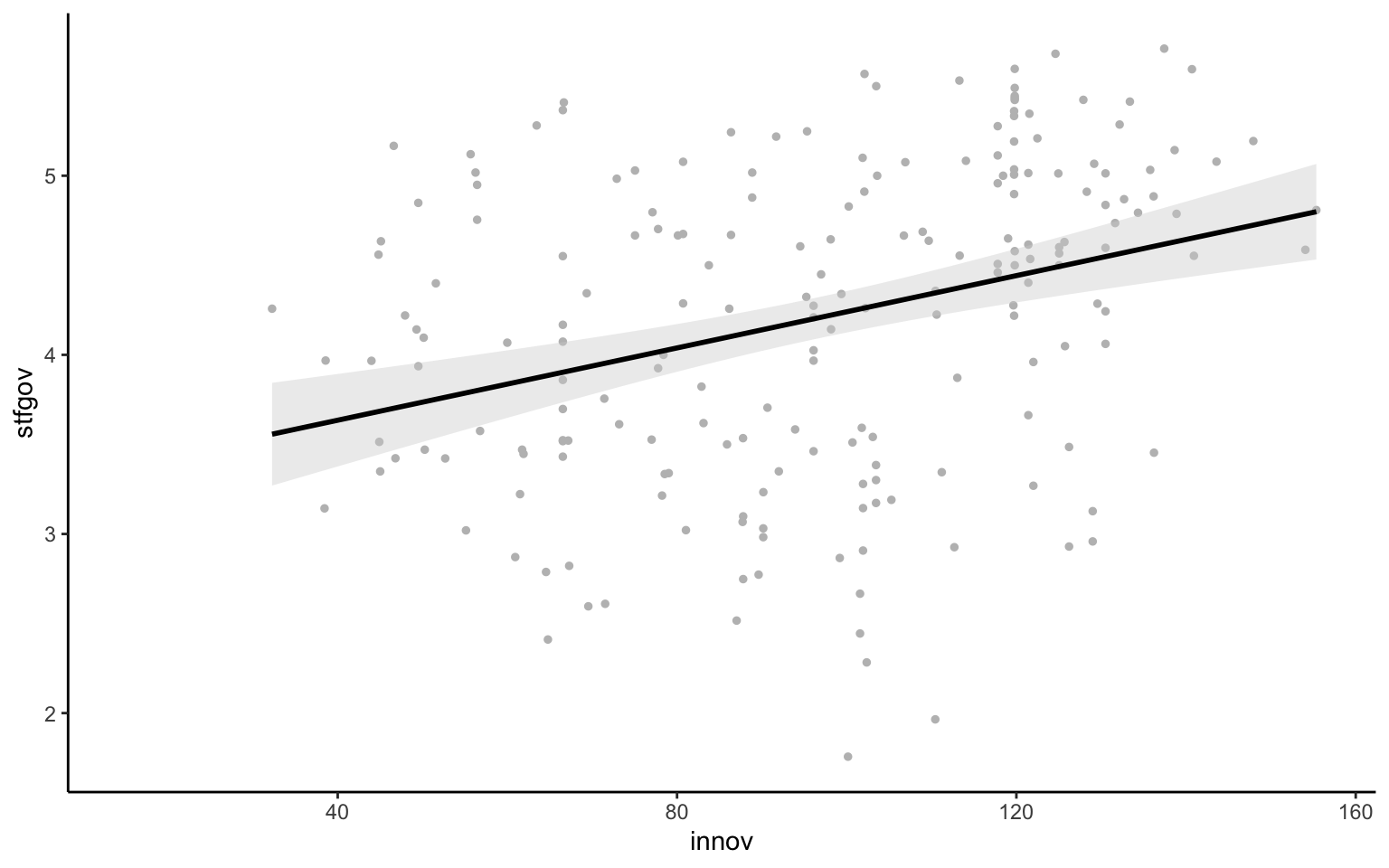

Figura 10.10: Definición de atributos, size

Finalmente, el atributo genérico alpha permite dar más o menos transparencia a la geometría. La transparencia hace referencia a qué grado de definición tiene el objeto o la capa en cuestión. Es especialmente útil cuando en una gráfica se quieren sobreponer diferentes capas de geometría o cuando se puede dar el caso de que hay muchas observaciones próximas y que pueden quedar superpuestas las unas con las otras. Para evitar que una parte de la información quede invisibilizada, la transparencia permite visualizar diferentes elementos superpuestos. La transparencia se define con un número entre el 0 y el 1; por defecto, el valor es 1, es decir, definición completa y objetos opacos, mientras que el valor 0 sería equivalente a definir color = NA y no mostrar la capa en cuestión. Los valores intermedios permiten mostrar la geometría con más o menos intensidad.

Los otros atributos que se pueden definir en las geometrías son más específicos en cada tipología de geometría definida:

shape. Usado en las geometrías de puntos, permite modificar la representación gráfica del punto, que por defecto es redondo. Con este argumento, se pueden modificar los puntos redondos por cuadrados, triángulos, diamantes, etc. ggplot2 proporciona 25 tipos diferentes de puntos. Para definir el tipo de punto que se quiere usar, se puede indicar con el número asociado a cada tipo; se puede consultar aquí) o escribiendo el nombre del tipo de punto que se quiere usar. Los puntos números 21 a 24 permiten definir tanto el color del borde como el color del relleno del punto.
linewidth. Usado en geometrías de líneas, permite modificar el grosor de la línea de manera similar a la definición del atributo size.
linetype. Usado en geometrías de líneas, permite definir la tipología de línea (continua, de puntos, de guiones…). Para conocer las diferentes posibilidades existentes, se puede consultar este enlace.
fontface. Usado en geometrías de texto, permite definir la representación del texto y mostrarlo en negrita o cursiva, por ejemplo. Se especifica indicando, entre comillas, alguna de las opciones siguientes: “plain”, “bold”, “italic”, “bold.italic”.

Siguiendo con el ejemplo anterior, nos puede interesar no solo obtener una gráfica en blanco y negro, sino también modificar la forma de los puntos, reducir su presencia en la gráfica e indicar la línea con un formato diferente. Una opción posible (figura 10.11) sería a partir del código siguiente:

nuts |> 
  ggplot(mapping = aes(x = innov, y = stfgov)) + 
  geom_point(shape = 21,
             size = 1,
             color = "darkgray",
             fill = "gray",
             alpha = 0.6)+
  geom_smooth(method = "lm",
              color = "black",
              fill="lightgray",
              linetype="dashed")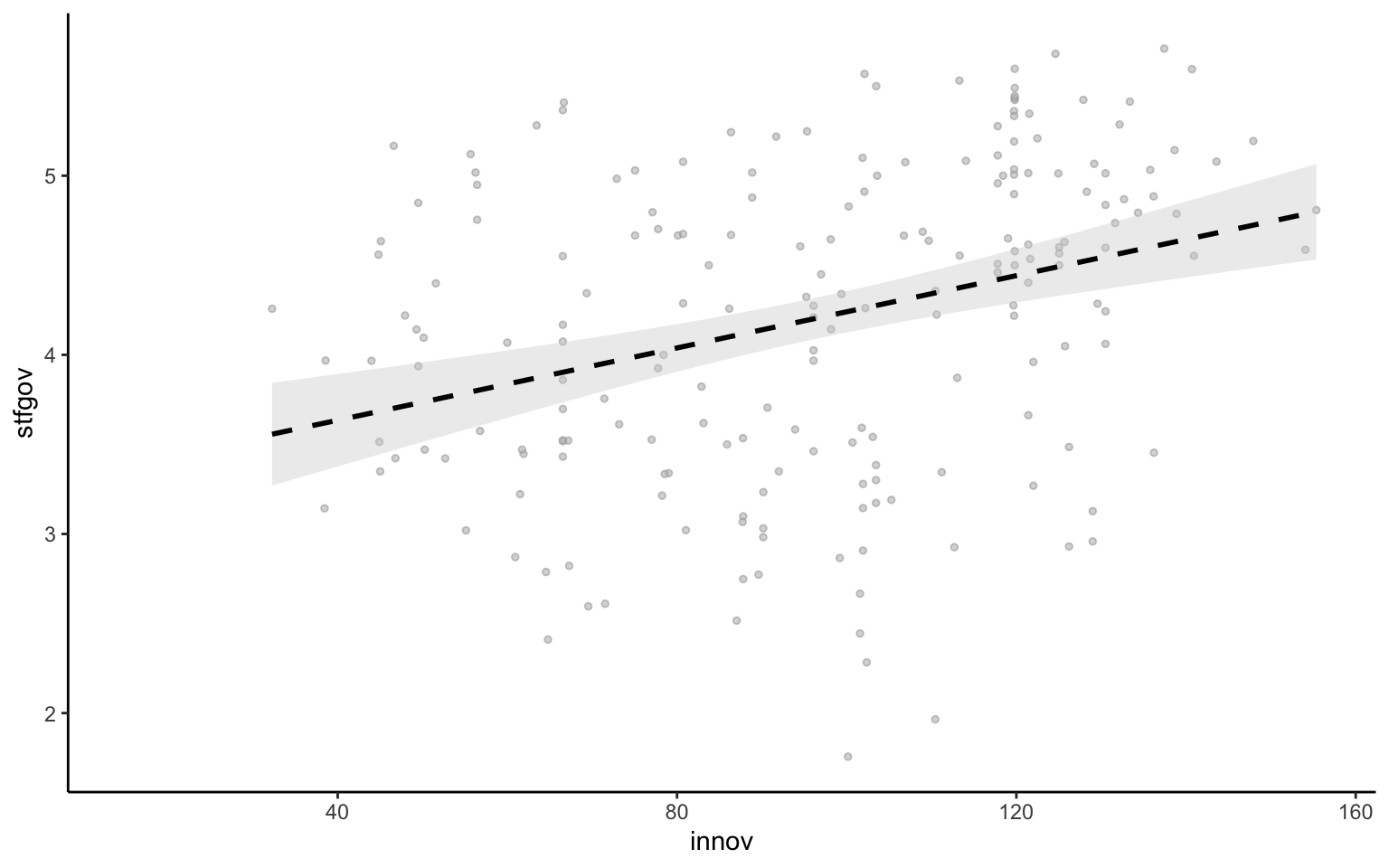

Figura 10.11: Definición de atributos, múltiples tipos

10.5 Añadir terceras variables

Hasta ahora todas las gráficas que se han generado representaban únicamente dos variables, una en cada eje, pero a veces puede ser interesante añadir más información en una gráfica. El hecho de trabajar con gráficas bidimensionales —las tridimensionales suelen ser bastante más complejas de interpretar— hace que la forma más habitual de añadir nuevas variables en una gráfica sea asociando algún elemento estético a una tercera variable. Ahora bien, es importante distinguir entre los cambios estéticos definidos por terceras variables y los cambios debidos a especificaciones estéticas de atributos.

10.5.1 Distinguir entre estéticos y atributos

Un elemento clave es que, cuando las terceras variables están representadas por un elemento estético, generarán cambios en alguno de los atributos especificando dos o más categorías —ya sean colores, formas, medidas, etc. Además, estos cambios asociados con terceras variables siempre se tendrán que indicar en la segunda capa, dentro de la función aes(). En cambio, cuando se quiere modificar algún elemento por razones meramente cosméticas:

Este cambio se aplicará a todos los casos por igual.
Se tiene que hacer desde la función de geometría.

Un ejemplo clarificará estas distinciones. La gráfica anterior mostraba unos datos en los que se disponía de información para cada región europea de diferentes atributos asociados a la región. Hasta el momento, se ha observado la relación entre los niveles de innovación y la satisfacción con el gobierno, pero ahora se quiere poder identificar los países (tercera variable) a los que pertenecen cada una de estas regiones. Una opción sería dar un color diferente a cada punto que identificara a cada uno de los países. Como lo que se quiere es añadir esta tercera variable a la gráfica, y se quiere hacer a partir de un elemento estético como el color, lo que se tiene que hacer es definir en la capa de proyección estética aes() que el color tiene que ir asociado a la variable país. En este caso, y para simplificar la gráfica de la figura 10.12, se ha optado por seleccionar la información de solo cuatro países (España, Francia, Italia y Portugal) y se define a partir de pipes.

nuts |> 
  filter(ccode %in% c('ES', 'FR', 'IT', 'PT') ) |> 
  ggplot(mapping = aes(x = innov, y = stfgov, color = country)) + 
  geom_point()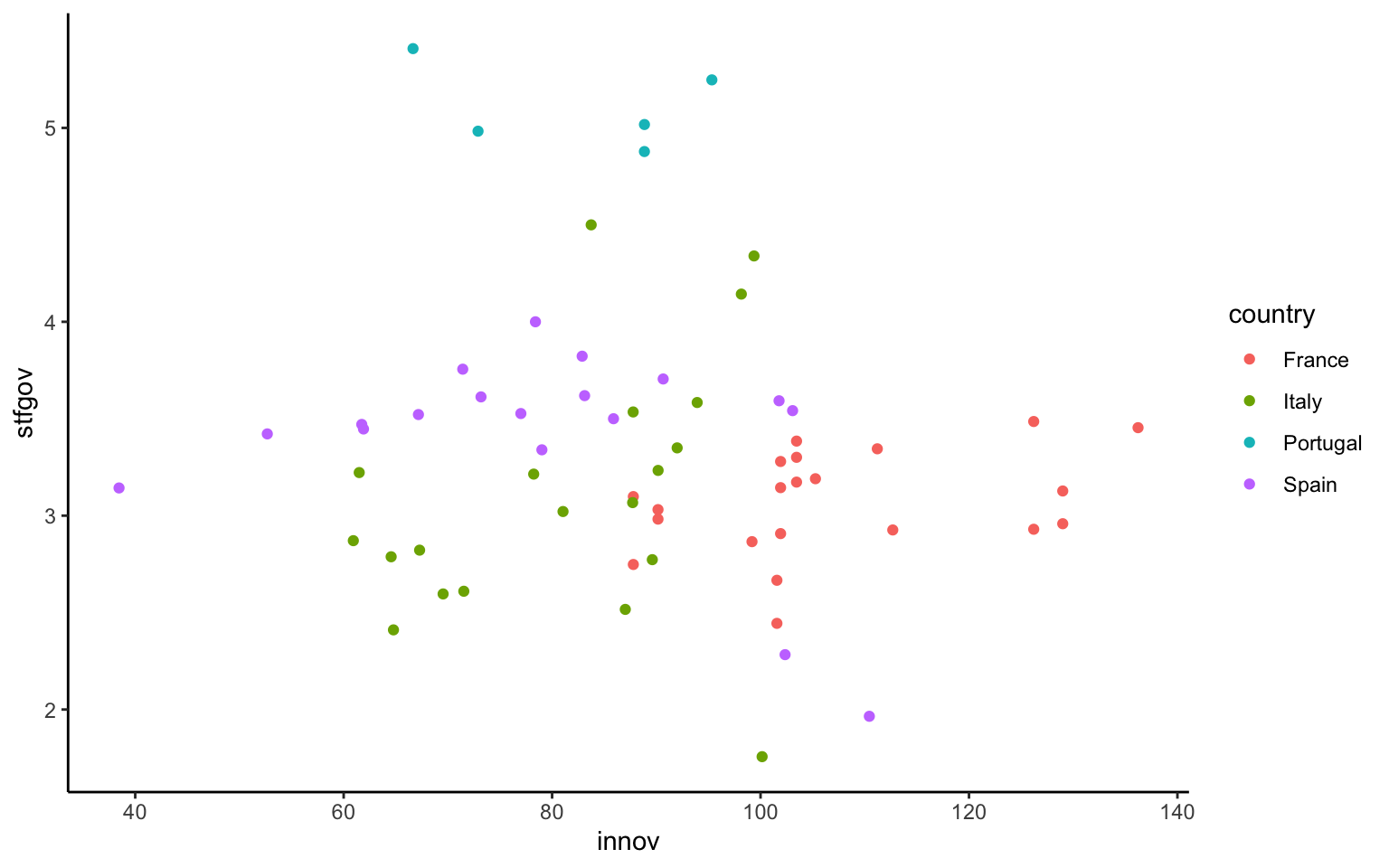

Figura 10.12: Tercera variable como proyección estética

Con este diagrama de dispersión, ya se pueden observar algunas diferencias entre países. Portugal es el país con una mayor satisfacción con el gobierno, y Francia es el país donde los niveles de innovación son más elevados. En cuanto a la relación entre las dos variables, parece que en Italia y Portugal la relación es positiva, en Francia prácticamente no hay relación y en España la relación parece ser negativa. Estas intuiciones se pueden confirmar si en la gráfica anterior se añade la capa de la relación lineal entre ambas variables, como vemos en la figura 10.13. En este caso, además, se ha definido un nivel de transparencia adecuado para poder seguir viendo todos los puntos del diagrama de dispersión.

nuts |> 
  filter(ccode %in% c('ES', 'FR', 'IT', 'PT') ) |> 
  ggplot(mapping = aes(x = innov, y = stfgov, color = country)) + 
  geom_point() +
  geom_smooth(method = "lm", alpha = 0.1)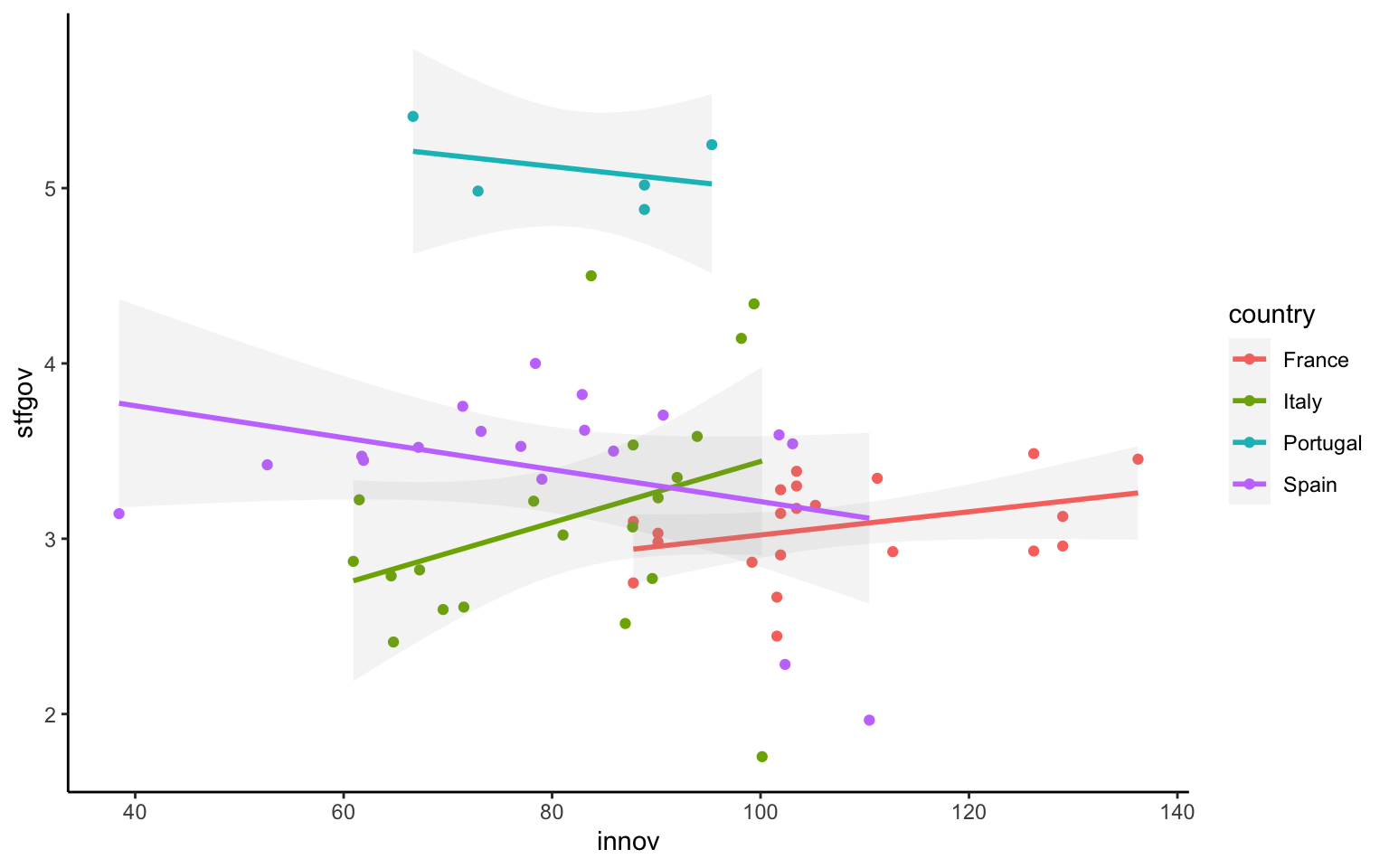

Figura 10.13: Tercera variable como proyección estética en dos geometrías

En esta última gráfica, el hecho de especificar una tercera variable en la capa de proyección estética relacionada con el color genera dos cambios diferentes. No solo cambia el color de los puntos, sino también el de las líneas, que pasan a ser tantas como colores hay en la gráfica. Cuando se define una tercera variable a partir de un elemento estético —en este caso el color—, esto se aplica a todas las capas de geometría que se incluyen en la gráfica y que son susceptibles de modificar este elemento estético. En el ejemplo anterior, como tanto el color de los puntos como el color de la línea se pueden modificar con el atributo de color, el color pasa a identificar cada una de las categorías de país. Esta gráfica, por lo tanto, permite distinguir, por un lado, de qué país son las regiones representadas por puntos y, por otro, cuál es la relación entre las dos variables para cada país a partir del color de las líneas.

Si, en cambio, el objetivo fuera simplemente identificar el país de cada una de las observaciones pero mostrar la relación lineal del conjunto de las observaciones, se podría definir la proyección estética de la tercera variable solo en una de las capas de la gráfica. Esto se podría hacer indicando la proyección estética dentro de la función de una de las geometrías. Por ejemplo, se podría optar por crear una gráfica con puntos de colores según el país, pero combinarlo con una única recta de relación lineal para el conjunto de casos. La figura 10.14 siguiente lo ejemplifica:

nuts |> 
  filter(ccode %in% c('ES', 'FR', 'IT', 'PT') ) |> 
  ggplot(mapping = aes(x = innov, y = stfgov)) + 
  geom_point(aes(color = country)) +
  geom_smooth(method = "lm", color = "black", alpha = 0.2)

Figura 10.14: Tercera variable como proyección estética en una única geometría

¿Atributo o estético?

Existe un pequeño truco para distinguir cuando el color —o cualquier otro elemento— se define como atributo o como proyección estética. Cuando se quiere definir un atributo, siempre se indica con una palabra entre comillas y, en cambio, cuando se define una proyección estética, siempre se la vincula a un objeto o variable del marco de datos. En el caso anterior, por ejemplo, el color de los puntos hace referencia a una tercera variable (country) que se escribe sin comillas e incidirá en la proyección estética y la información que transmite la gráfica. En cambio, el color de la línea hace referencia a un atributo específico de la geometría, y se indica el color ("black") entre comillas.

La gráfica anterior muestra que las proyecciones estéticas, especialmente las referentes a terceras variables, se pueden indicar tanto en la función ggplot(), si el objetivo es aplicarlas a todas las capas geométricas, como en la capa geométrica en cuestión, indicando la función aes() dentro de la función geom_...().

10.5.2 Diferentes formas de añadir terceras variables

El ejemplo que se ha usado hasta ahora nos ha permitido distinguir los datos a partir de una tercera variable —concretamente, de tipo categórico— usando el color. Esta no es la única manera de distinguir la información que se produce como consecuencia de la introducción de una tercera variable. A continuación, se presentan otras formas de incorporar terceras variables en una gráfica.

10.5.2.1 Color

La proyección estética de color no solo permite clasificar las observaciones (los puntos del diagrama de dispersión) cuando la tercera variable es categórica. También es posible hacerlo cuando esta tercera variable es cuantitativa continua. Por ejemplo, si la gráfica tiene que representar la relación entre innovación y satisfacción con el gobierno sobre la base de la latitud de las regiones —¿estas regiones se sitúan más al norte o más al sur?—, se puede pedir una gráfica donde el color sea un gradiente. En esta escala de colores, los más oscuros indicarían regiones que se sitúan más al sur y los colores más claros, las regiones nórdicas⁴.

⁴ Se excluyen de la gráfica los territorios de ultramar de Francia.

nuts |> 
  filter(lat > 20) |> # Excluyendo los territorios de ultramar
  ggplot(mapping = aes(x = innov, y = stfgov, color = lat)) + 
  geom_point()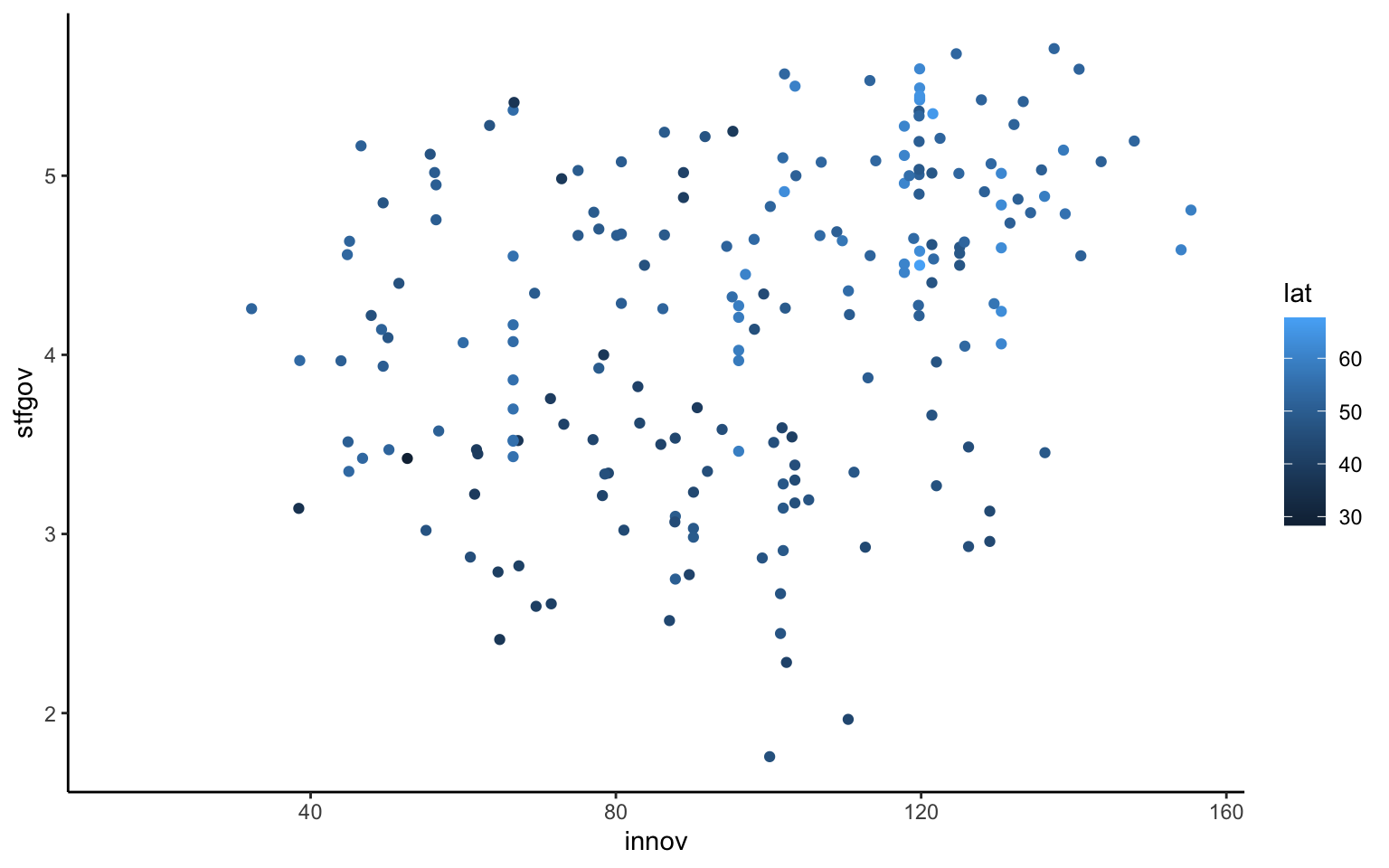

Figura 10.15: Tercera variable como proyección estética (gradiente de color)

El resultado de la figura 10.15 muestra que la mayoría de las regiones nórdicas tienen niveles más elevados de innovación y de satisfacción con el gobierno. En este caso, no existe un color específico para cada categoría, sino que, como la variable para definir la proyección estética es continua, ggplot2 interpreta automáticamente que tiene que implementar un gradiente de color. Esta escala de colores da una información adicional a la hora de representar gráficamente la información.

10.5.2.2 Tamaño (size)

Una forma equivalente de incluir terceras variables ordenables en una gráfica es a partir del tamaño de la geometría. Por ejemplo, en el caso del diagrama de dispersión empleado hasta el momento, si se quisiera evaluar si el vínculo emocional con Europa incide en la relación entre innovación y satisfacción con el gobierno, se podría representar modificando el tamaño de los puntos de la gráfica en función de si el vínculo con Europa es bajo (punto pequeño) o es elevado (punto grande) en cada una de las regiones. El resultado sería el siguiente (figura 10.16):

nuts |> 
  ggplot(mapping = aes(x = innov, y = stfgov, size = atcherp)) + 
  geom_point()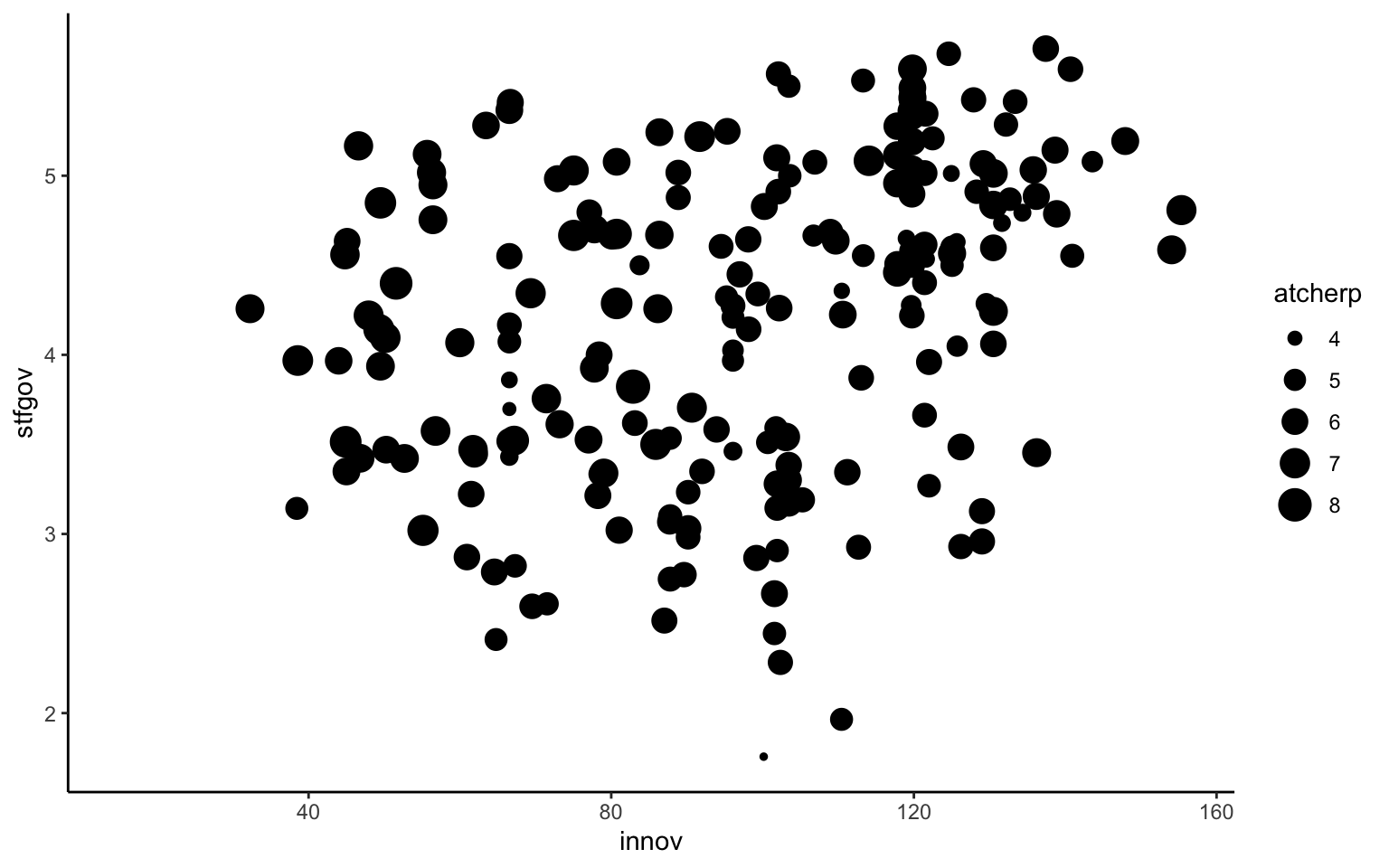

Figura 10.16: Tercera variable como proyección estética (size)

10.5.2.3 Forma (shape)

Dejando de lado el uso de terceras variables de tipo cuantitativo y volviendo a emplear variables de tipo categórico, otra opción para distinguir las observaciones es usando las diferentes formas disponibles para representar un punto en las coordenadas de la gráfica. Así, y volviendo al ejemplo anterior en que la tercera variable correspondía a los países, se podría representar la gráfica de la forma siguiente:

nuts |> 
  filter(ccode %in% c("ES", "FR", "IT", "PT")) |> 
  ggplot(mapping = aes(x = innov, y = stfgov, shape = country)) + 
  geom_point()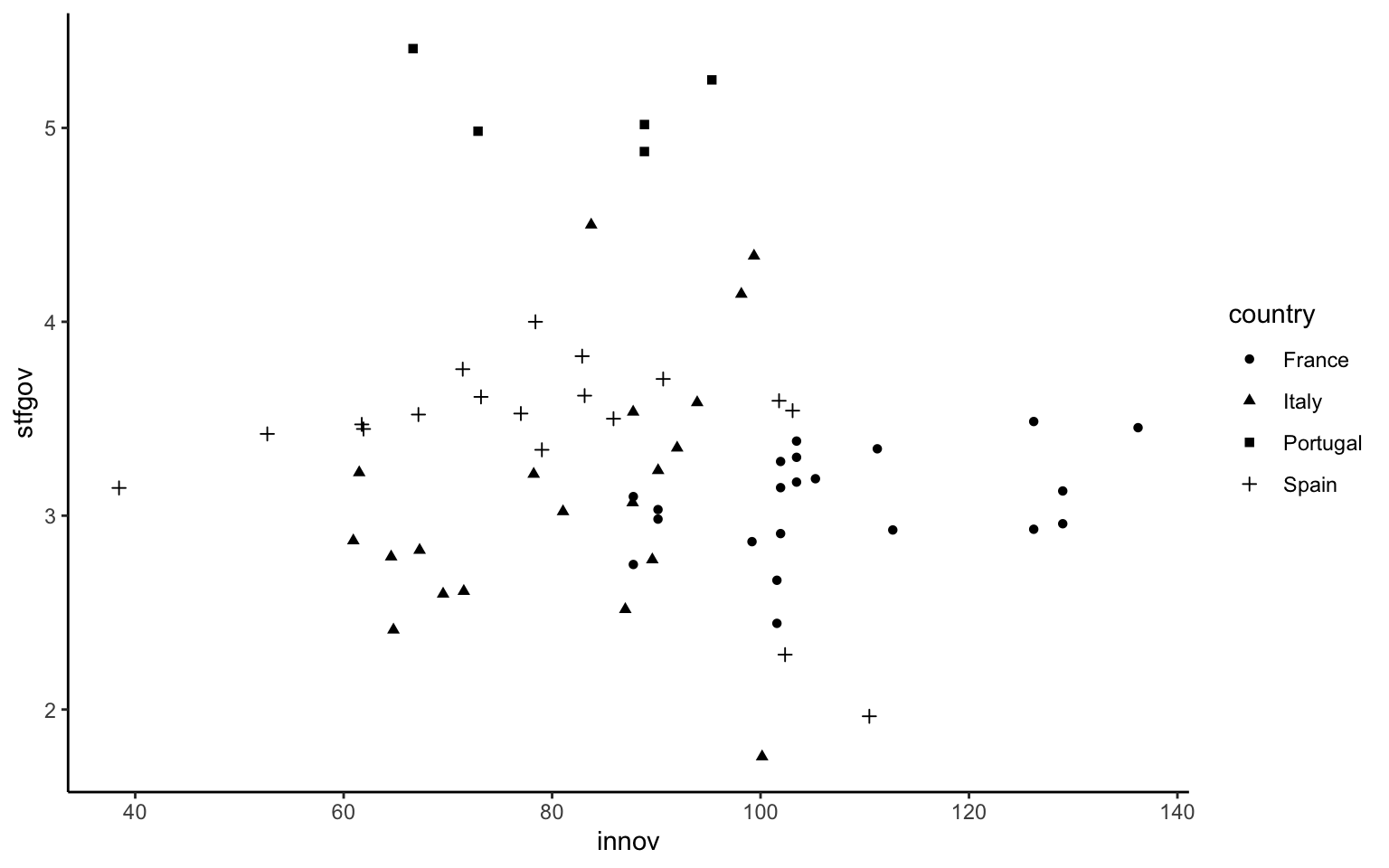

Figura 10.17: Tercera variable como proyección estética (shape)

En esta representación de la figura 10.17, cada observación tiene una forma diferente en función de si la región pertenece a un país u otro. A la hora de definir esta proyección estética a partir de la forma, es importante tener presente que, por defecto, ggplot2 solo representa como máximo seis categorías diferentes, puesto que considera que cuando existen más de seis formas diferentes es más difícil de interpretar adecuadamente la gráfica. Por lo tanto, esta solución es solo válida para casos en que la tercera variable es de tipo categórico y, lo que es importante, tiene pocas categorías. Si bien es cierto que se puede definir de manera manual qué formas se asocien a cada categoría —se podría hacer si hay más de seis categorías—, el modo de hacerlo se escapa del alcance de este curso y no sería muy recomendable.

10.5.2.4 Texto

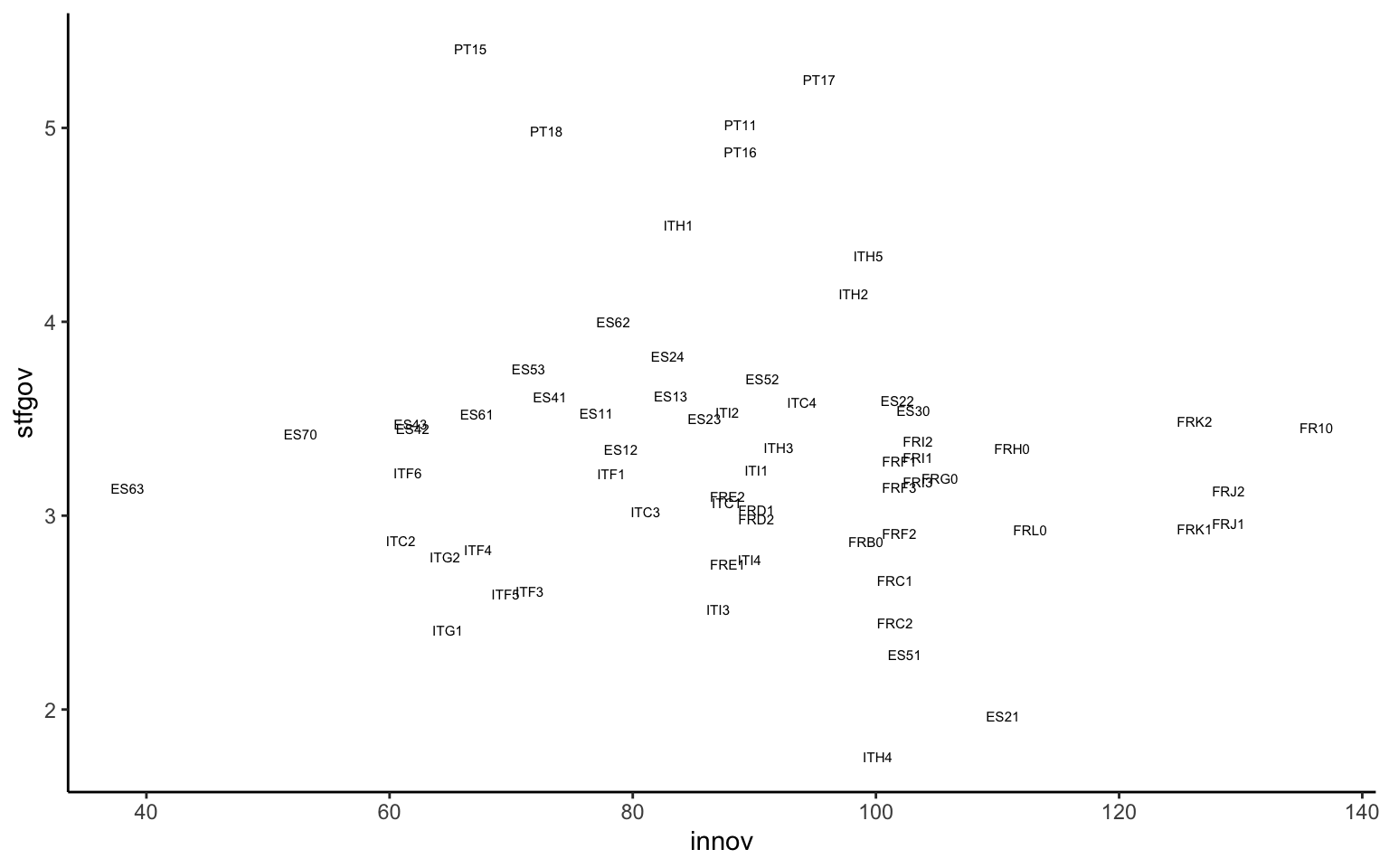
Otra forma interesante de representar las variables es a partir de texto. En algunas ocasiones puede ser interesante representar las diferentes observaciones de alguna manera que nos permita identificar alguna característica única de cada observación. Por ejemplo, se podría pensar en poner una etiqueta con el nombre de cada una de las regiones. Para poderlo hacer, hay que añadir a la gráfica una proyección geométrica específica que permita la adición de texto: geom_text(). Si se replica la gráfica de la relación entre innovación y satisfacción con el gobierno en los cuatro países seleccionados anteriormente y se añade el texto que se quiere, se obtiene una gráfica como la de la figura 10.18:

nuts |> 
  filter(ccode %in% c("ES", "FR", "IT", "PT")) |> 
  ggplot(mapping = aes(x = innov, y = stfgov, label = name)) + 
  geom_point() +
  geom_text()

Figura 10.18: Tercera variable como proyección estética (texto 1)

La adición estética de la etiqueta no afecta a la función geom_point() porque no tiene asociado ningún argumento de label, pero sí que afecta a la función geom_text(). A pesar de que muestra lo que se buscaba, esta gráfica es problemática por dos razones. Por un lado, el texto de los nombres de las regiones es demasiado grande e impide la lectura de los nombres de las regiones. Por otro lado, el texto se sobrepone al punto. Ambos problemas dificultan la comprensión e interpretación de la gráfica, pero no suframos, tienen solución. Para el primer problema, simplemente se puede reducir el tamaño del texto con el argumento size. Para el segundo problema, se puede pensar en dos soluciones: o bien se elimina de la gráfica la capa de puntos, puesto que el texto del nombre de las regiones se centrará justo en la ubicación del punto, o bien se indica que el texto se tiene que situar a una distancia determinada del punto. Si se opta por esta segunda opción, se puede usar el argumento nudge_y, que permite definir una distancia vertical respecto a la ubicación original del texto (figura 10.19).

nuts |> 
  filter(ccode %in% c("ES", "FR", "IT", "PT")) |> 
  ggplot(mapping = aes(x = innov, y = stfgov, label = name)) + 
  geom_point() +
  geom_text(size = 2, nudge_y = 0.07)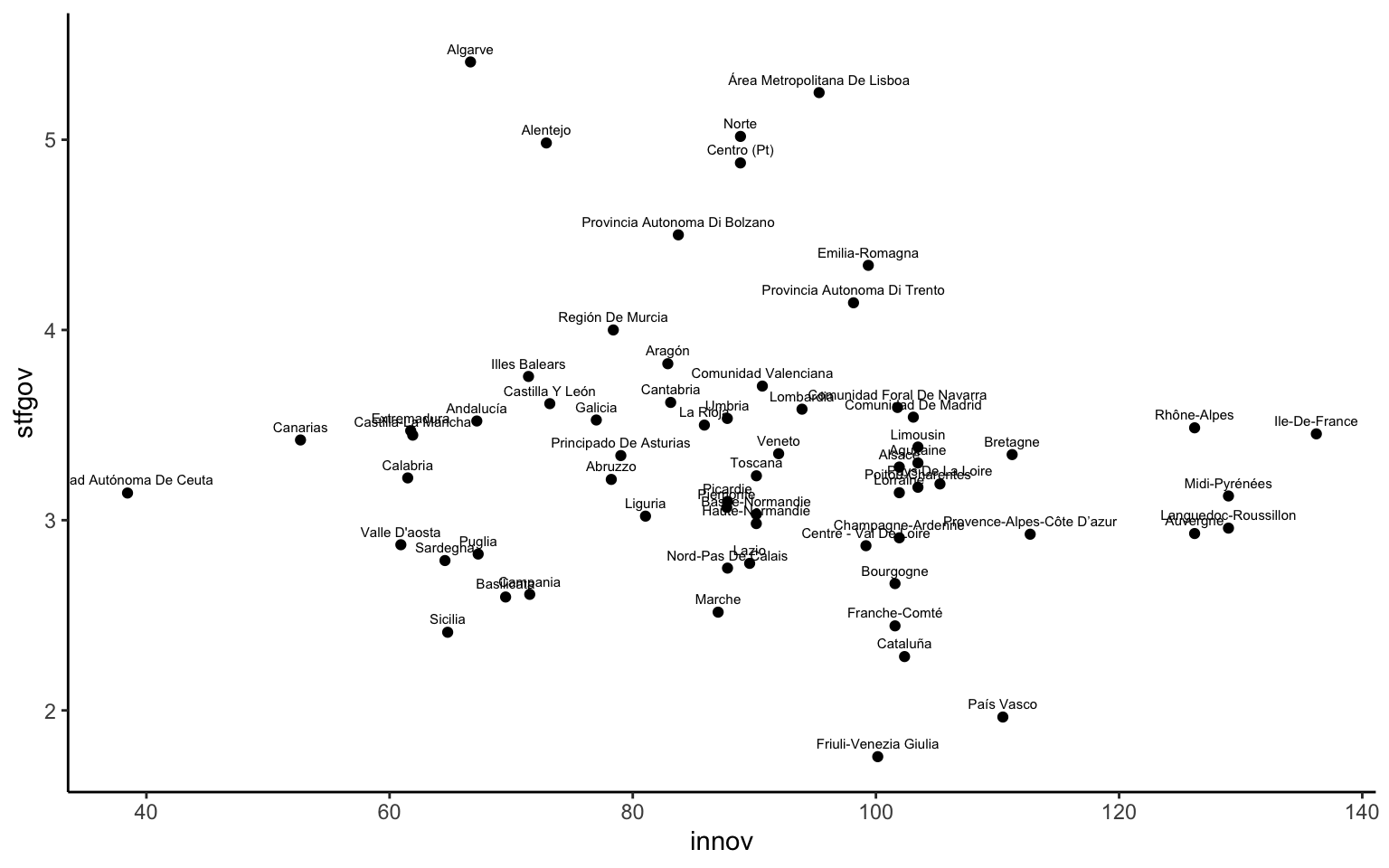

Figura 10.19: Tercera variable como proyección estética (texto 2)

A pesar de que en las zonas donde hay más acumulación de observaciones sigue siendo difícil leer el texto, para las observaciones más extremas sí que es posible identificarlas. Una de las recomendaciones cuando se usa texto es intentar usar identificadores textuales que sean breves, como las siglas. Por ejemplo, una opción sería elaborar la misma gráfica pero usando la variable geo que indica el código NUTS de cada región. Además, como se ha mencionado antes, y para simplificar, también se podría eliminar la capa de la geometría de puntos (figura 10.20).

nuts |> 
  filter(ccode %in% c("ES", "FR", "IT", "PT") ) |> 
  ggplot(mapping = aes(x = innov, y = stfgov, label = geo)) +
  geom_text(size = 2)

Figura 10.20: Tercera variable como proyección estética (texto 3)