8 Variables numéricas
8.1 Introducción
Cuando tenemos delante una variable numérica, se nos presenta un reto parecido al que nos hemos encontrado en el apartado anterior. Si desplegamos la variable, solo veremos una secuencia de números que se repiten raramente. Y de nuevo, es necesario utilizar varias técnicas que nos permitan extraer información sintetizada. Existen tres categorías principales de medidas cuantitativas que nos proporcionan información sobre cómo están distribuidos los valores de una variable numérica: las medidas de centralidad, las medidas de dispersión y las medidas de localización.
La aplicación de estas técnicas nos permite obtener resúmenes numéricos de una variable. Por ejemplo, gracias a los instrumentos del análisis univariado, podríamos calcular la media de edad de toda la población de Cataluña si dispusiéramos de las edades de todos sus habitantes. Sin embargo, una medida como la media adquiere mucho más sentido cuando se compara con las medias de otros grupos. Por este motivo, para interpretar si la media de edad de Cataluña es elevada o baja, es útil disponer de información de otras poblaciones como punto de referencia. Así pues, cuando hacemos un análisis univariado en este ejemplo, recogemos información por edades de toda la población en España. A continuación, calcularemos las medias agrupadas por comunidad autónoma. La comparación entre grupos siempre nos dará más contexto para los datos que estamos analizando. En este apartado aprenderemos qué técnicas tenemos al alcance, y en el próximo apartado (Resumir y agrupar) aprenderemos a usar estas técnicas para comparar entre subgrupos.
8.2 Medidas de centralidad
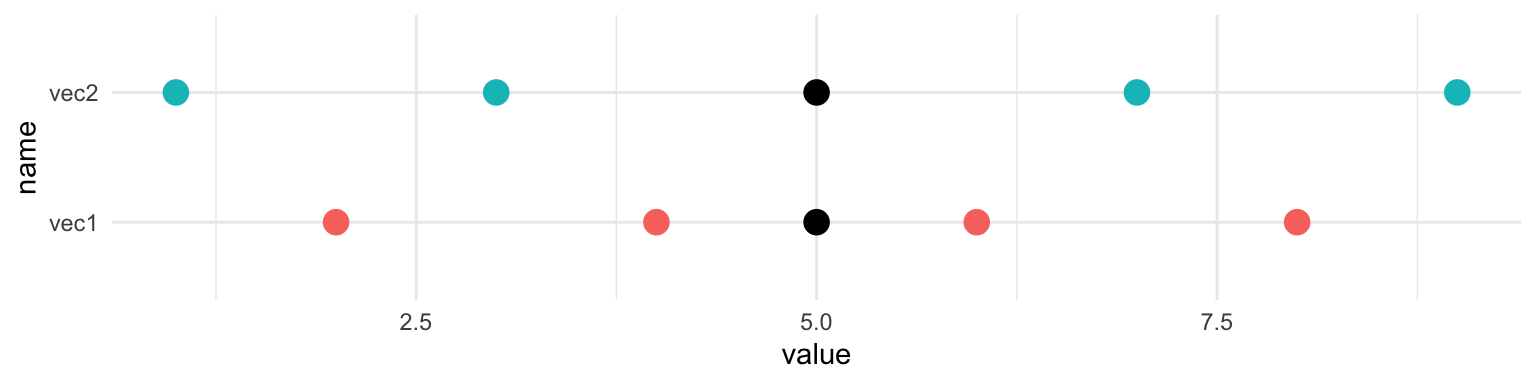
Las medidas de centralidad nos proporcionan un punto de referencia o un valor central que representa típicamente la distribución de los datos. Encontrar “el centro” de una distribución no es tan fácil como puede parecer. Fijémonos en el equipo de baloncesto que tenemos en el margen de la derecha (figura 8.1). Al primer golpe de vista, vemos que es una distribución formada por cinco observaciones, que varían en la altura. En orden de izquierda a derecha, las observaciones miden respectivamente 170, 185, 162, 190 y 183 centímetros de altura.
Esta variable la representaremos en el vector bsk siguiente:
bsk <- c(170, 185, 162, 190, 183)¿Cuál es el centro de esta distribución? Para encontrar la respuesta a la pregunta, tendríamos que definir algún procedimiento que nos permita cuantificar y resumir la información de esta variable en un solo número. Y, de hecho, la pregunta no tiene una sola respuesta, puesto que no hay una sola manera de sintetizar esta distribución en un valor que sea representativo de todos los casos. Como siempre, la respuesta depende de la pregunta. Y hay tres preguntas que nos podemos hacer:
¿Cuál es el valor que se repite más veces? Como ya hemos visto en el apartado anterior, esto se denomina moda. Y, como veremos, la moda es un poco más complicada de encontrar en variables numéricas.
¿Cuál es el valor de media que asigna de forma equitativa la suma de los valores de la distribución entre el total de casos? Este valor es la media, seguramente el estadístico descriptivo por excelencia.
¿Cuál es el valor que se encuentra en medio de la distribución cuando ordenamos todos los casos de menos a más? Esto se denomina mediana.
8.2.1 La moda
La moda es el valor o valores que aparecen con más frecuencia en una distribución. Como hemos visto anteriormente, la moda es relativamente sencilla de encontrar en una variable categórica, puesto que la obtendremos simplemente buscando cuál es la categoría con más frecuencias. En cambio, encontrar la moda en una variable numérica no es un ejercicio tan evidente. Tenemos que pensar que estas variables pueden adoptar un número infinito de valores y, por lo tanto, es poco probable encontrar algún número repetido, y, si se da el caso, no nos aportará información muy relevante.
Fijémonos en qué pasa si pedimos una tabla de frecuencias para encontrar la moda de la variable bsk. Vemos que todos los valores se repiten una vez. Por lo tanto, no hay moda. Y esto será lo habitual en variables numéricas, donde, si se repite algún valor, será fruto más de la coincidencia que no de algún factor relevante.
A veces sí que puede tener sentido pedir las frecuencias de una variable numérica siempre que tengan un número de valores reducido: por ejemplo, las variables de intervalo como Polity (tiene 21 valores) o la variable edad (raramente tendrá más de 90 valores).
table(bsk)
## bsk
## 162 170 183 185 190
## 1 1 1 1 1En variables con más valores nos encontramos con el mismo problema. A continuación, hemos pedido las frecuencias de la variable freehms del marco de datos nuts. Esta variable mide el grado de intolerancia de la población de la región respecto a los gais y las lesbianas1. Un valor próximo a 1 significa que la población es de media muy tolerante, mientras que un valor próximo a 5 significa que la población es de media muy intolerante. Si realizamos un recuento con count(), vemos que algunos valores se repiten dos veces. Pero el hecho de que se repitan es principalmente fruto de la casualidad, y esto no nos aporta ninguna información sobre los datos.
1 Específicamente, se pregunta hasta qué punto se está de acuerdo con que los gais y las lesbianas vivan su propia vida como quieran.
Así pues, no tiene mucho sentido buscar el valor más repetido en las variables numéricas. En cambio, sí que tendrá más sentido observar visualmente dónde se encuentran concentrados los valores de la variable. Este ejercicio lo podemos hacer fácilmente con un histograma, que nos permitirá visualizar cuál es el punto más alto de la distribución. El histograma representa, en el eje horizontal, un conjunto de barras verticales con diferentes intervalos. En el eje vertical, la altura de cada barra representa la frecuencia o la cantidad de observaciones que recaen dentro de este intervalo.
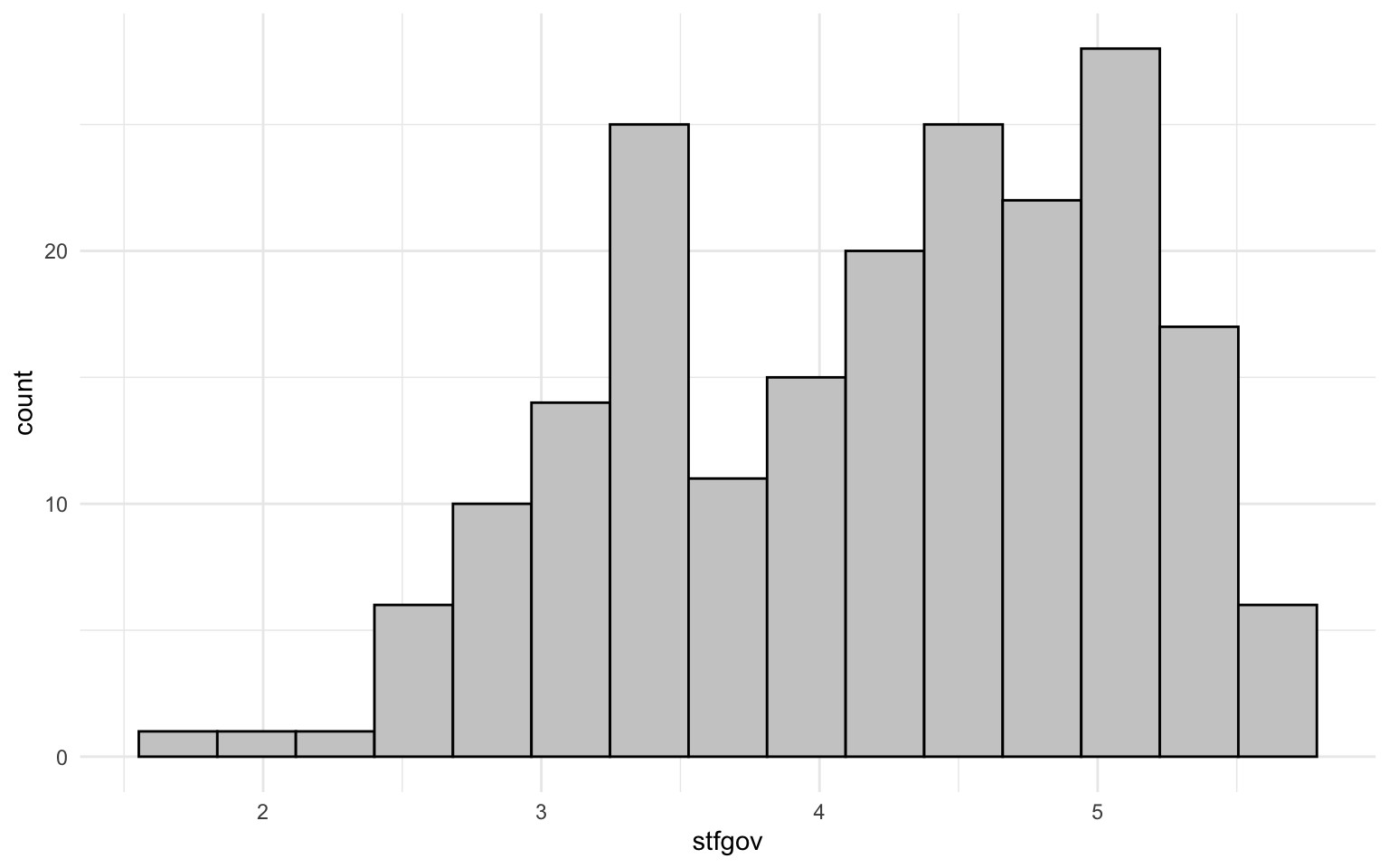
La forma más rápida para crear un histograma es con la función hist(). Con el primer argumento, indicaremos la variable que queremos representar en formato dólar y, opcionalmente, con el segundo argumento (breaks), el número de intervalos en que quedará cortada la variable. Si lo aplicamos a la variable freehms e indicamos que queremos visualizar siete intervalos, observamos que hay aproximadamente 30 regiones que se sitúan en el intervalo de 1 a 1.5, que indica las regiones que de media tienen un nivel muy alto de tolerancia respecto a los gais y las lesbianas. Aquí la moda, entendida como el intervalo en el que se encuentra la mayor concentración de valores, se situaría entre 1.5 y 2, donde encontramos más de 80 observaciones.
hist(nuts$freehms, breaks = 7)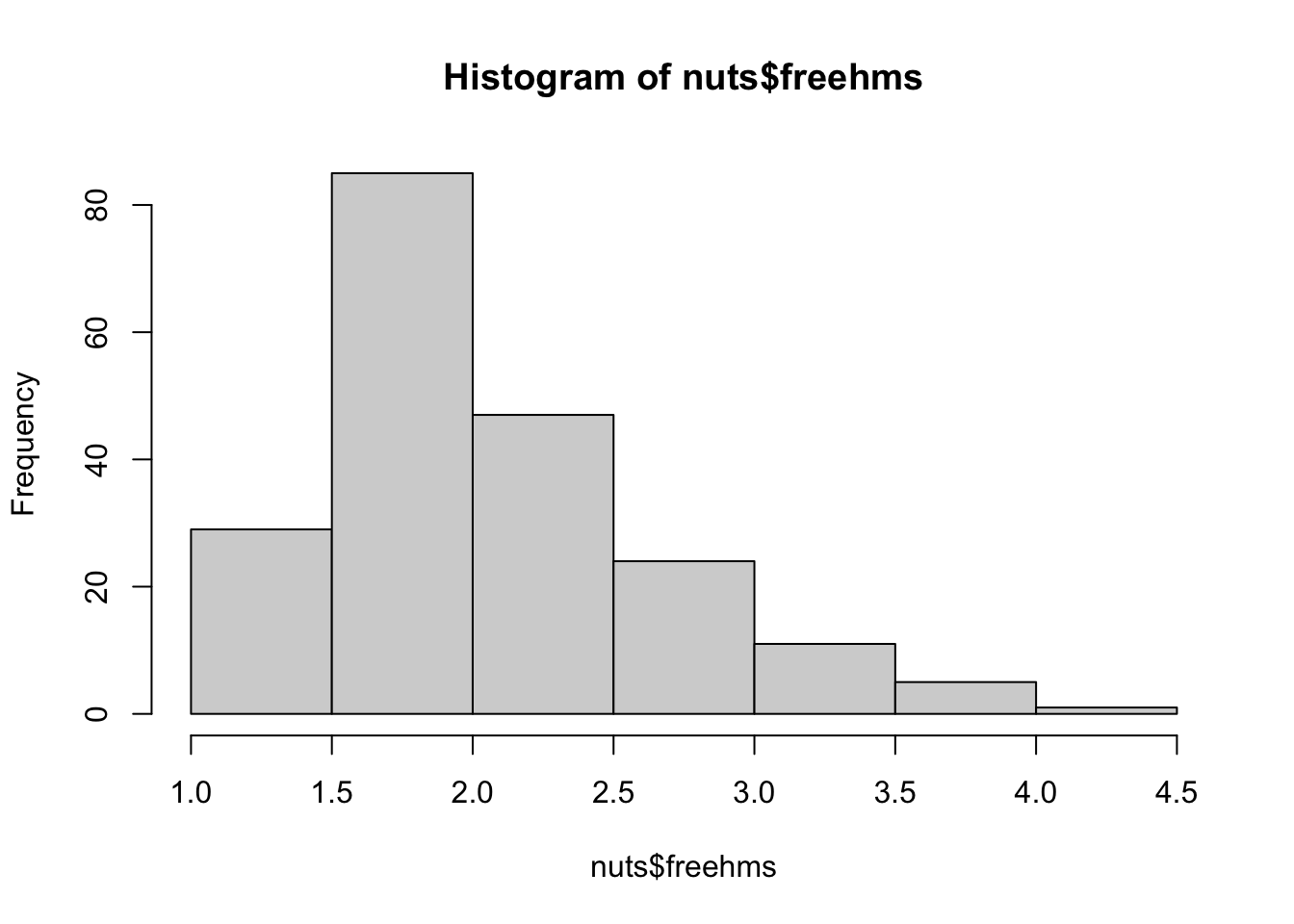
Existen dos diferencias principales entre el histograma y el diagrama de barras. En primer lugar, en el histograma las etiquetas del eje horizontal están situadas entre las barras porque representan la división entre intervalos; en cambio, en el diagrama de barras las etiquetas están situadas dentro de las barras del diagrama de barras porque representan la categoría. En segundo lugar, en el histograma las barras no están separadas, mientras que sí lo están en el diagrama de barras.
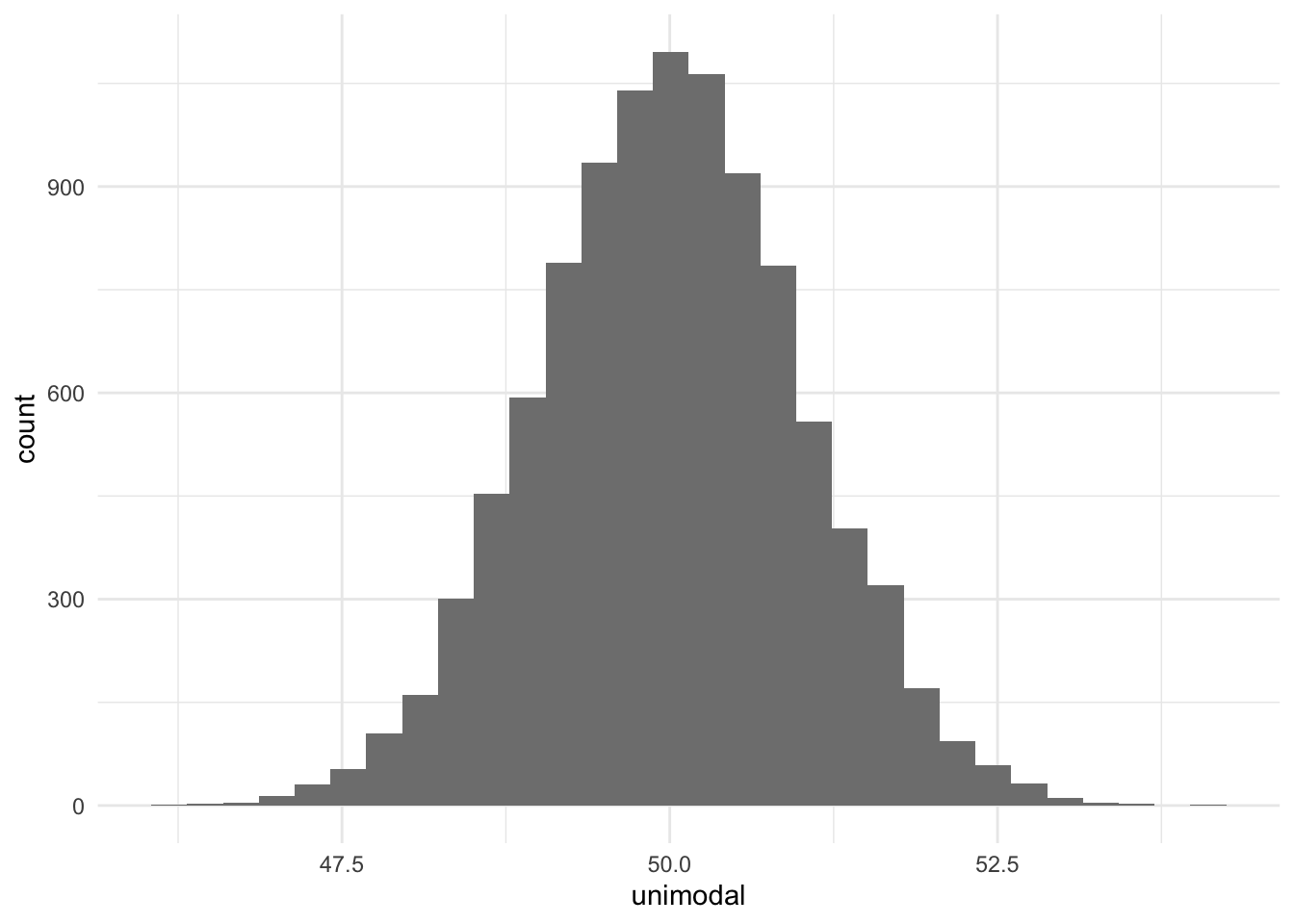
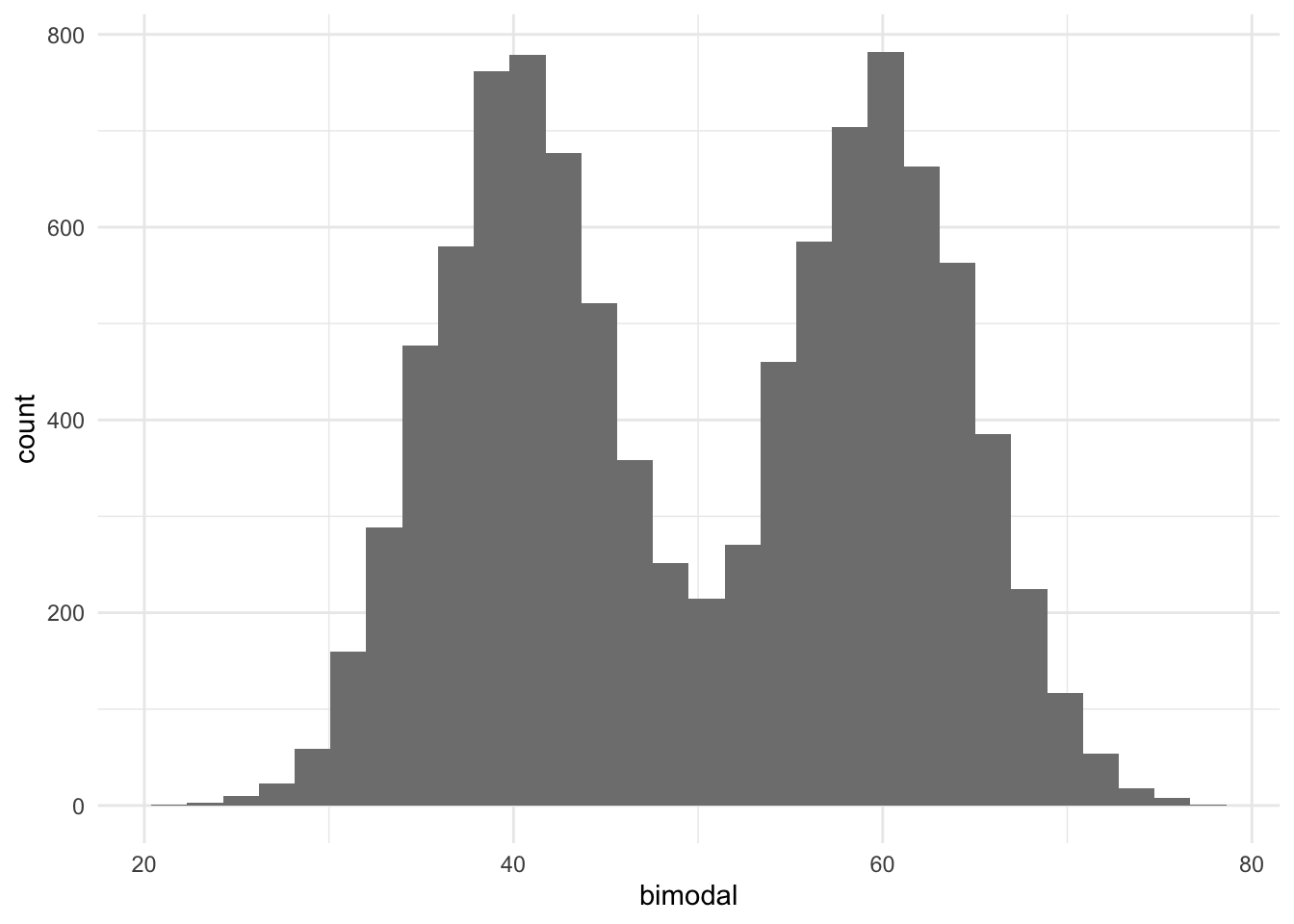
El histograma, pues, nos da una visión general de cómo están distribuidas las observaciones de una variable numérica y nos indica dónde se encuentra la concentración de casos mayor. Sin embargo, nos podemos encontrar en varias situaciones en las que no hay claramente una moda. En la figura 8.2 podemos observar los diferentes tipos de distribuciones que pueden dar lugar a diferentes tipos de modas. Cuando solo observamos una punta, es decir, una concentración clara de casos en el gráfico, lo llamaremos distribución unimodal (a). Cuando observamos dos modas, lo llamaremos bimodal (b). La distribución será multimodal (c) cuando hay más de dos puntas identificables, y será uniforme (d) cuando no se aprecie ninguna punta relevante concreta.
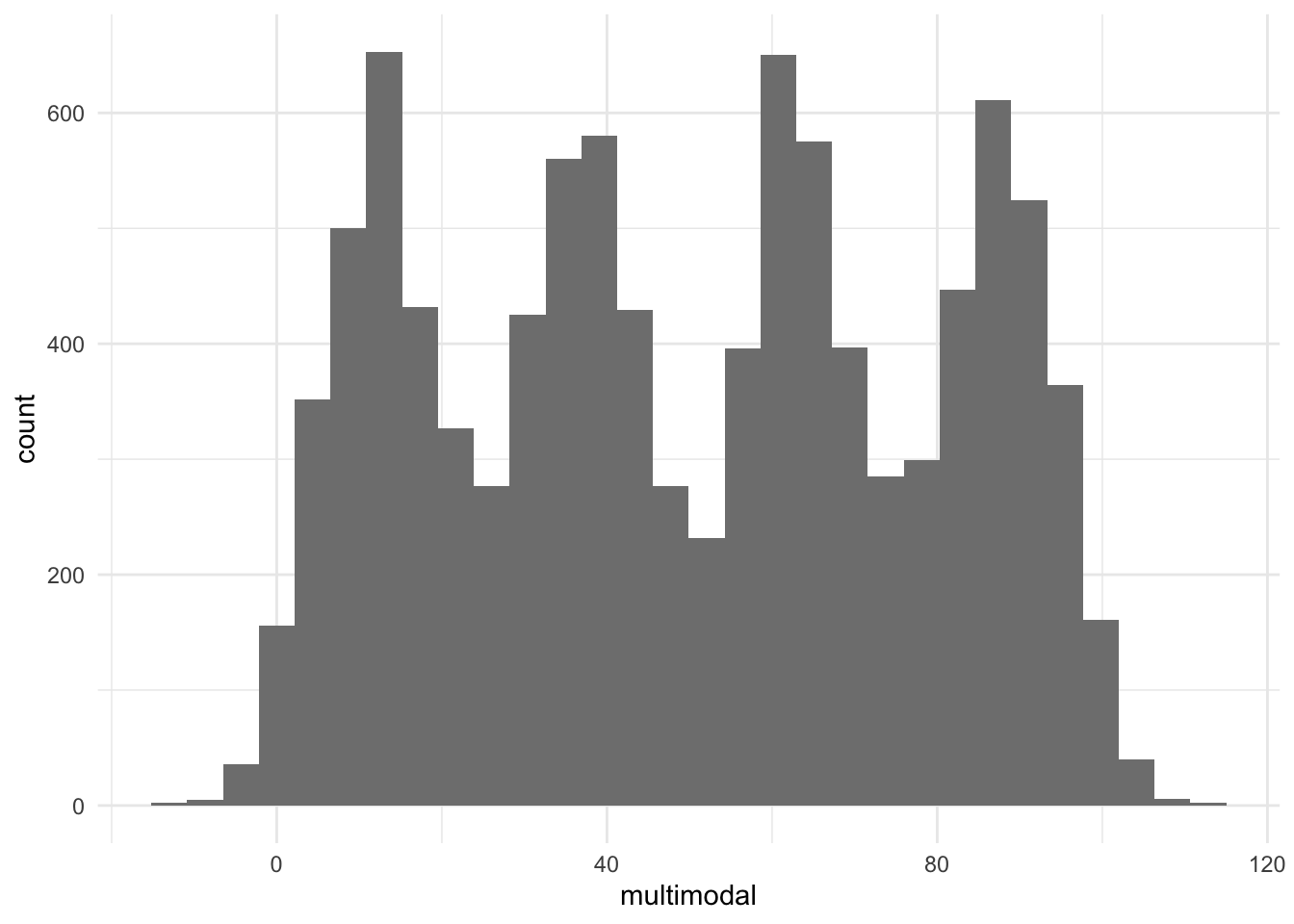
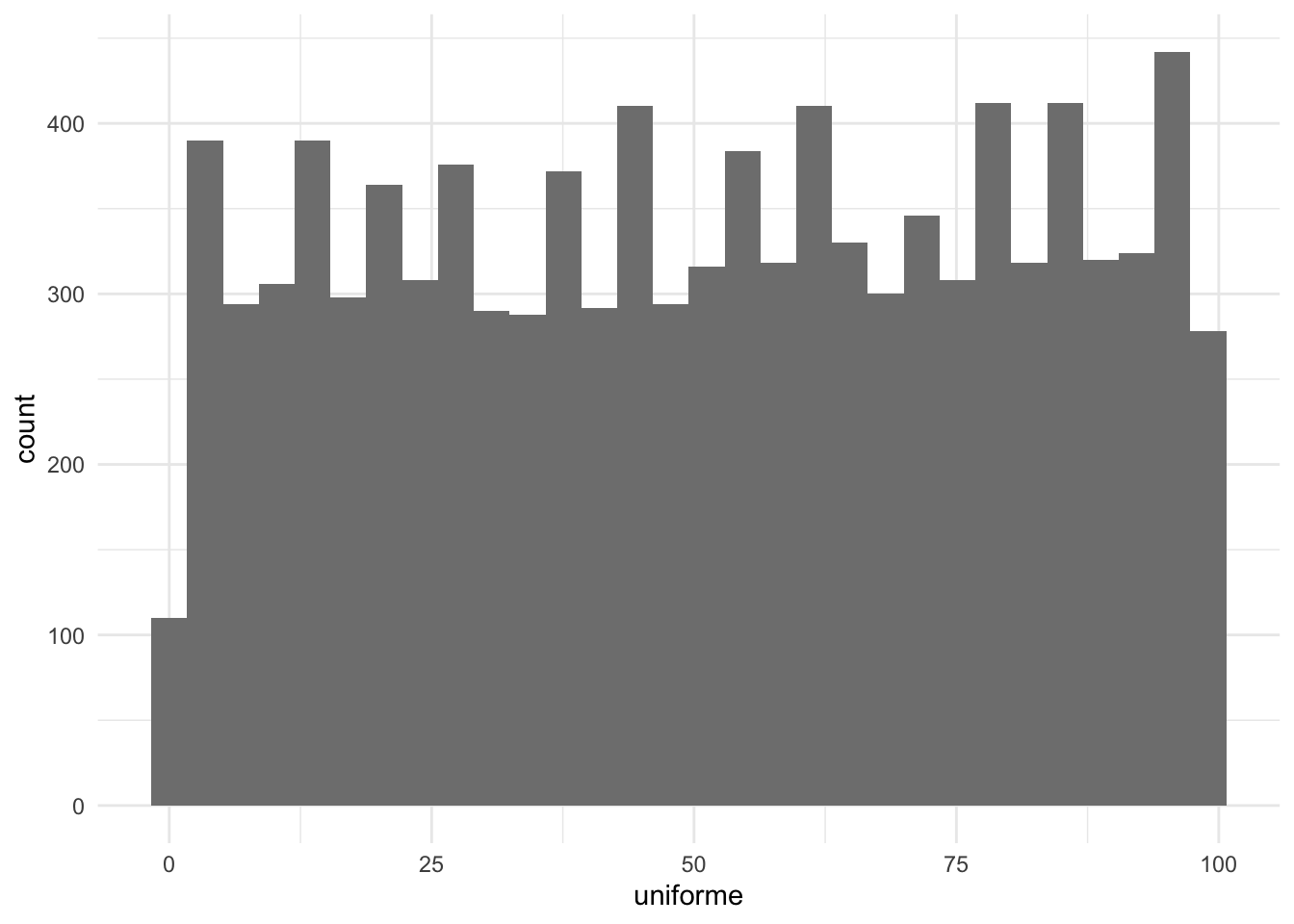
Por ejemplo, en la figura 8.3 observamos la distribución de la satisfacción respecto al gobierno por regiones de la Unión Europea. Cada observación es la media de satisfacción respecto al gobierno en una región concreta. Podríamos decir que esta distribución es bimodal (o incluso multimodal si consideramos que hay tres puntas). En escala de 0 a 10, el intervalo de valores más repetido se sitúa cerca de 5. Pero también hay otro grupo de países en el que el intervalo de casos se repite con frecuencia, que se sitúa cerca de 3.5.
8.2.2 La media
La media es una de las medidas de tendencia central más utilizadas para resumir distribuciones. La media nos dice cuál sería el valor que obtendríamos si niveláramos el peso de cada valor de la distribución entre sus casos. Una forma muy ilustrativa de entender qué representa la media es mediante la distribución de la riqueza de un país. En cualquier país, la riqueza acostumbra a estar distribuida de manera desigual. Hay individuos que tienen más dinero y hay otros que tienen menos. Lo que nos dice la media es cuánto dinero le tocaría a cada habitante si cogiéramos el dinero de toda la población y lo repartiéramos a partes iguales. En todas las distribuciones, la media hace exactamente esto: suma todos los valores y los divide entre el total de frecuencias.
Si cogemos las alturas del equipo de baloncesto y las repartimos entre los cinco miembros del equipo (figura 8.4), de forma que los jugadores más altos cedan una parte de su altura a los jugadores más bajos hasta distribuir equitativamente la altura entre todos los jugadores, la altura media del equipo sería 178 centímetros. Esta cifra se calcula sumando todos los valores de la variable y dividiéndolos por el número total de casos.
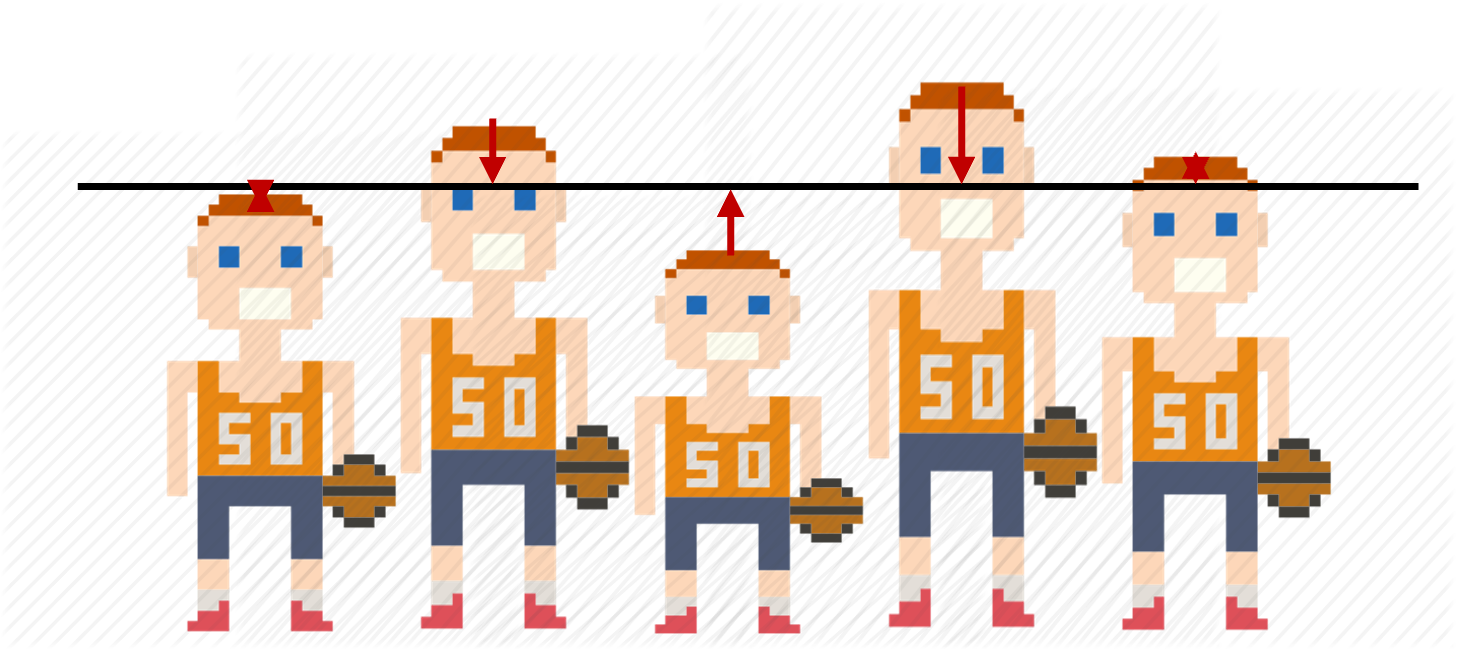
Una forma más sencilla y directa de hacer este cálculo es con la función mean(). A continuación, hemos aplicado la función al objeto bsk que habíamos creado anteriormente, y esto nos permite obtener también la cifra de 178 centímetros.
mean(bsk)
## [1] 178Cuando calculamos medias en marcos de datos relativamente grandes, como los que estamos trabajando, es muy probable que haya observaciones con valores perdidos (también denominados NA). Es por eso que siempre será preferible introducir un segundo argumento, na.rm = T, para eliminar los valores perdidos a la hora de hacer el cálculo de la media. Contrariamente, el resultado será NA, como observamos en el código siguiente, que calcula la media del PIB per cápita de las observaciones del marco de datos nuts.
8.2.3 Mediana
La mediana indica qué valor tiene la observación que se encuentra exactamente en medio de una distribución ordenada. Lo veremos claramente si nos volvemos a fijar en el ejemplo del equipo de baloncesto. Esta vez, hemos ordenado la distribución de menos a más altura (figura 8.5). La mediana es la altura del individuo que se encuentra en medio de la distribución cuando la ordenamos. Por lo tanto, si nos fijamos en el vector bsk ordenado, la mediana se encontraría en el valor 183.
sort(bsk)
## [1] 162 170 183 185 190
Ordenar largos vectores de datos y encontrar el valor que se encuentra en la mitad puede ser un trabajo pesado. Por eso tenemos la función median(), que nos ayuda a calcular la mediana más rápidamente.
median(bsk)
## [1] 183Si la longitud del vector es par, nos encontramos con el problema que no hay un único valor central en una distribución ordenada, sino dos. No obstante, debemos tener presente que la diferencia entre estos dos valores será mínima. Un procedimiento habitual es calcular la media de estas dos medianas.
Con median(), podemos calcular la mediana del vector nuts$gdpcap_nuts. Fijaos que, en este caso, el valor central de la distribución es muy diferente si lo calculamos a través de la media (21.640 €) que si lo calculamos con la mediana (17.300 €).
median(nuts$gdpcap_nuts, na.rm = T)
## [1] 17300¿Cuál es mejor, pues, la mediana o la media? La respuesta es que depende de la pregunta que nos formulemos. Habitualmente, nosotros estamos acostumbrados a pensar en términos de medias cuando pensamos en una medida sintética de una variable numérica. No obstante, la mediana también es una medida muy importante en varios ámbitos. En algunos países, por ejemplo, el salario mínimo interprofesional o el umbral de pobreza se calculan a partir de la mediana2.
2 Más adelante, en la sección Las desigualdades: la media y mediana, veremos algunas cuestiones prácticas importantes sobre estas diferencias.
La mediana también es un concepto fundamental en uno de los teoremas clásicos de la ciencia política. El teorema del votante mediano (median voter) se refiere a la persona que se encuentra en medio de la distribución ideológica, típicamente en el eje izquierda-derecha. Dicho de otro modo, si ordenamos toda la población por ideología, el votante mediano es la persona que tiene tanta gente ideológicamente a la derecha como a la izquierda. En un sistema político bipartidista, el partido que consiga convencer al votante mediano será el que ganará las elecciones, dando por sentado que todos los votantes que estén a la izquierda del votante mediano votarán al partido progresista y todos los votantes que estén a su derecha votarán al partido conservador. Aquí radica la importancia del votante mediano, puesto que es el que decantará las elecciones y, por lo tanto, el objetivo principal de los partidos durante la campaña electoral.
8.2.4 Forma de la distribución y valores extremos
Hasta aquí ya hemos aprendido que en una distribución numérica la media no coincide necesariamente con la mediana. Y, de rebote, también podemos pensar que la mediana y la media no coinciden necesariamente con la moda. Es decir, tenemos tres maneras de calcular el centro de una distribución, y, por lo tanto, nos podemos encontrar con distribuciones que tienen tres centros diferentes. ¿De qué depende, pues, que la moda, la media y la mediana estén o no alineadas?
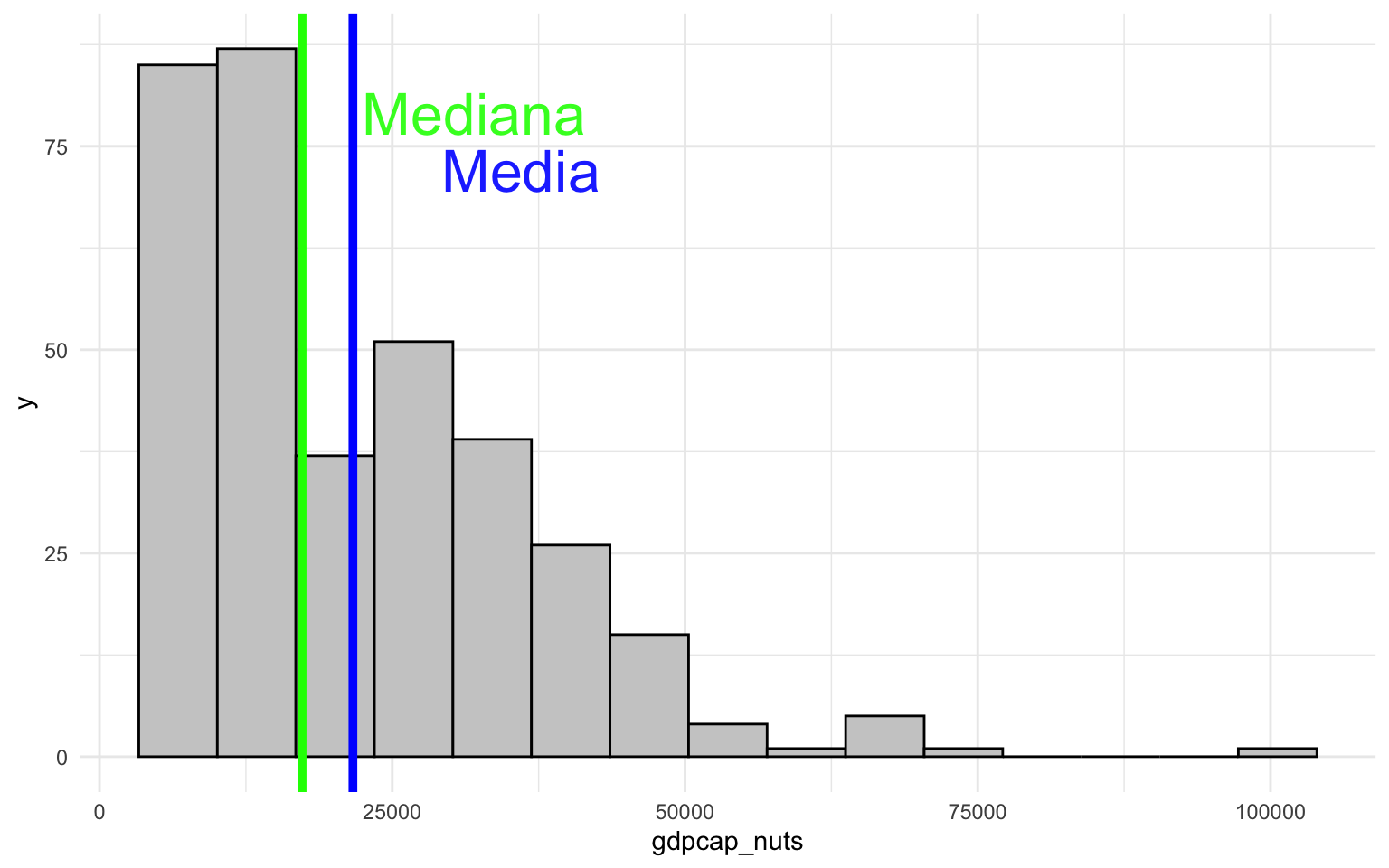
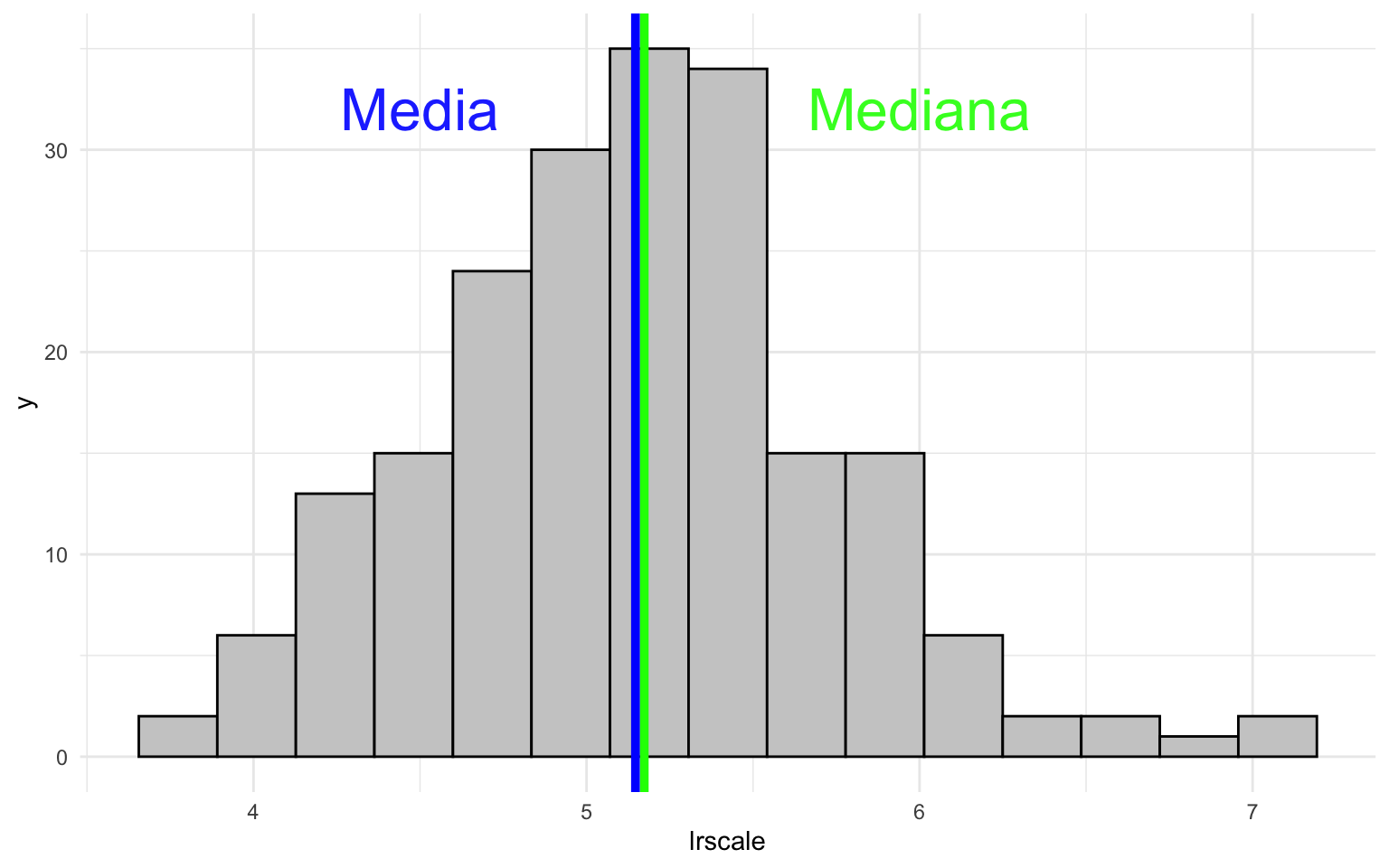
El principal motivo por el que la moda, la media y la mediana pueden divergir es por una mayor presencia de casos en un extremo de la distribución. Fijémonos en la figura 1, donde observamos el histograma de tres variables del marco de datos nuts, con la media marcada en azul y la mediana en verde. En el gráfico del medio (b) se representa la variable lrscale y observamos lo que se denomina una distribución simétrica. Esta distribución tiene la característica que las observaciones están distribuidas igualmente alrededor de un punto central, de forma que los valores a un lado y otro del centro son parecidos. Una distribución simétrica tiene la característica que la media y la mediana coinciden, y es probable que la moda también coincida.
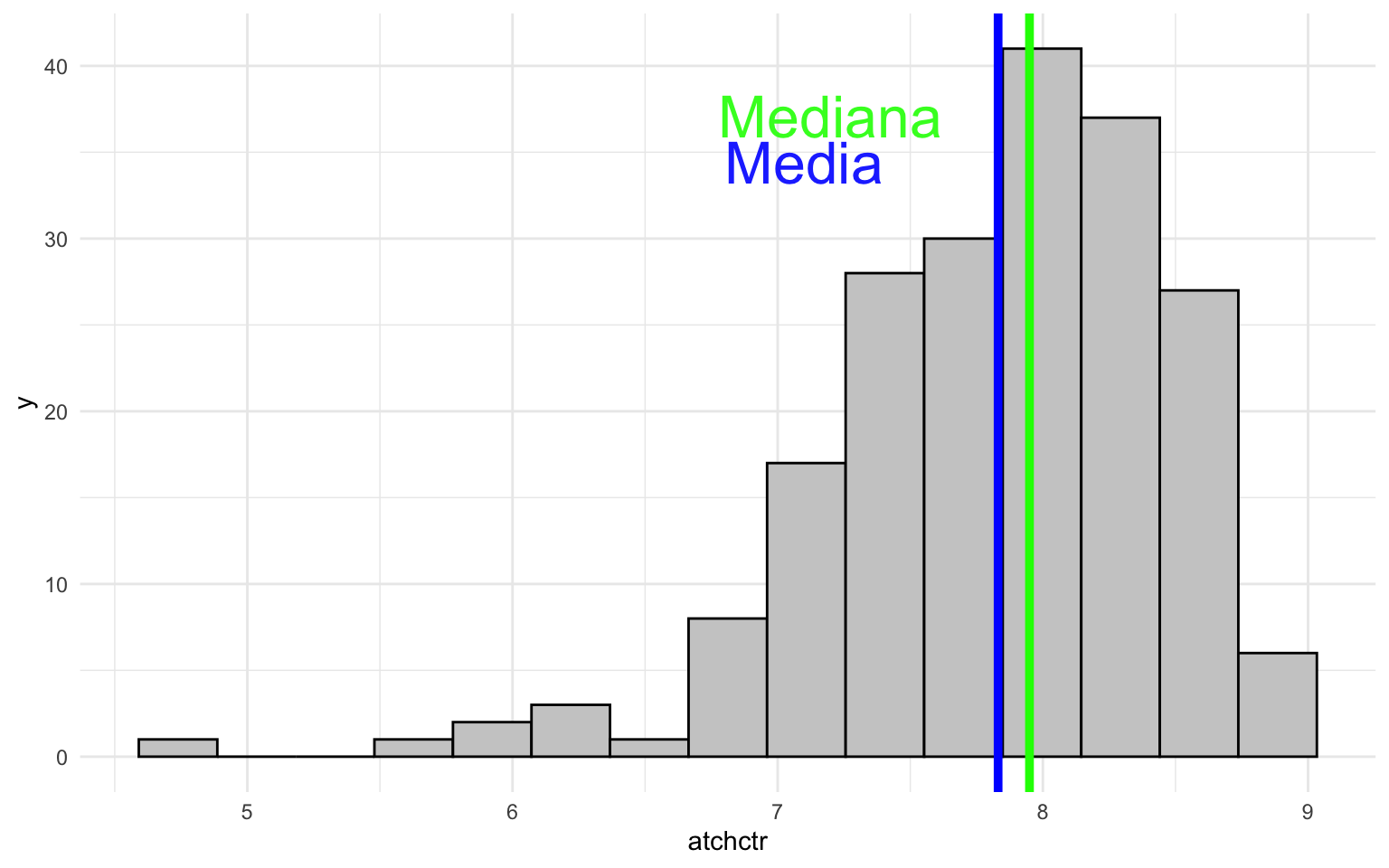
En el gráfico de la izquierda (a) (gdpcap_nuts) observamos lo que se denomina una distribución con asimetría negativa. En este caso, la mayoría de los casos se encuentra concentrada en la parte izquierda del gráfico, mientras que en la parte derecha podemos observar algunos valores extremos. Fijémonos, por ejemplo, que hay una o varias observaciones situadas cerca de 100.000 euros y que están muy alejadas del centro de la distribución. En este caso, la media tendrá un valor más alto que la mediana. En el gráfico de la derecha, en cambio, pasa justo lo contrario. En esta distribución tiene asimetría positiva, porque la mayoría de las observaciones están situadas a la derecha del gráfico, mientras que en la parte izquierda solo encontramos unos pocos casos. También observamos la presencia de algún valor extremo en regiones que tienen un nivel de adhesión en el estado inferior a 5. En este caso, la mediana tendrá un valor superior a la media3.
3 A menudo, para visualizar mejor estas distribuciones y hacer pruebas de significación estadística, se acostumbra a transformar la variable. En los casos de distribuciones con asimetría negativa, se aplica la escala logarítmica con las funciones log(), log2() o log10(), mientras que en distribuciones con asimetría positiva se puede aplicar el exponencial con la función exp().
¿Y por qué divergen la media y la mediana? El principal motivo es que la media es sensible a valores extremos y la mediana no. Para entenderlo fácilmente, observamos la figura 8.7, donde hemos sustituido el jugador más alto de nuestro equipo de baloncesto por uno de extremadamente alto. Para calcular la mediana, solo hay que ordenar la distribución y medir la altura del jugador del medio. Como el jugador del medio es el mismo que el de la figura 8.5, la mediana continúa siendo exactamente la misma. La presencia de un caso extremo no modifica el valor de la mediana. En cambio, la media sí que se ve afectada por valores extremos, porque esta medida de centralidad reparte a partes iguales entre las observaciones la suma de valores de la distribución. Esto hace que la presencia de un caso extremo en el extremo superior arrastre la media hacia valores más altos y mantenga inalterada la mediana. Es famoso el chiste entre la comunidad estadística que, cuando Bill Gates entra en un pub, todo el mundo que está dentro se convierte, de media, en millonario.
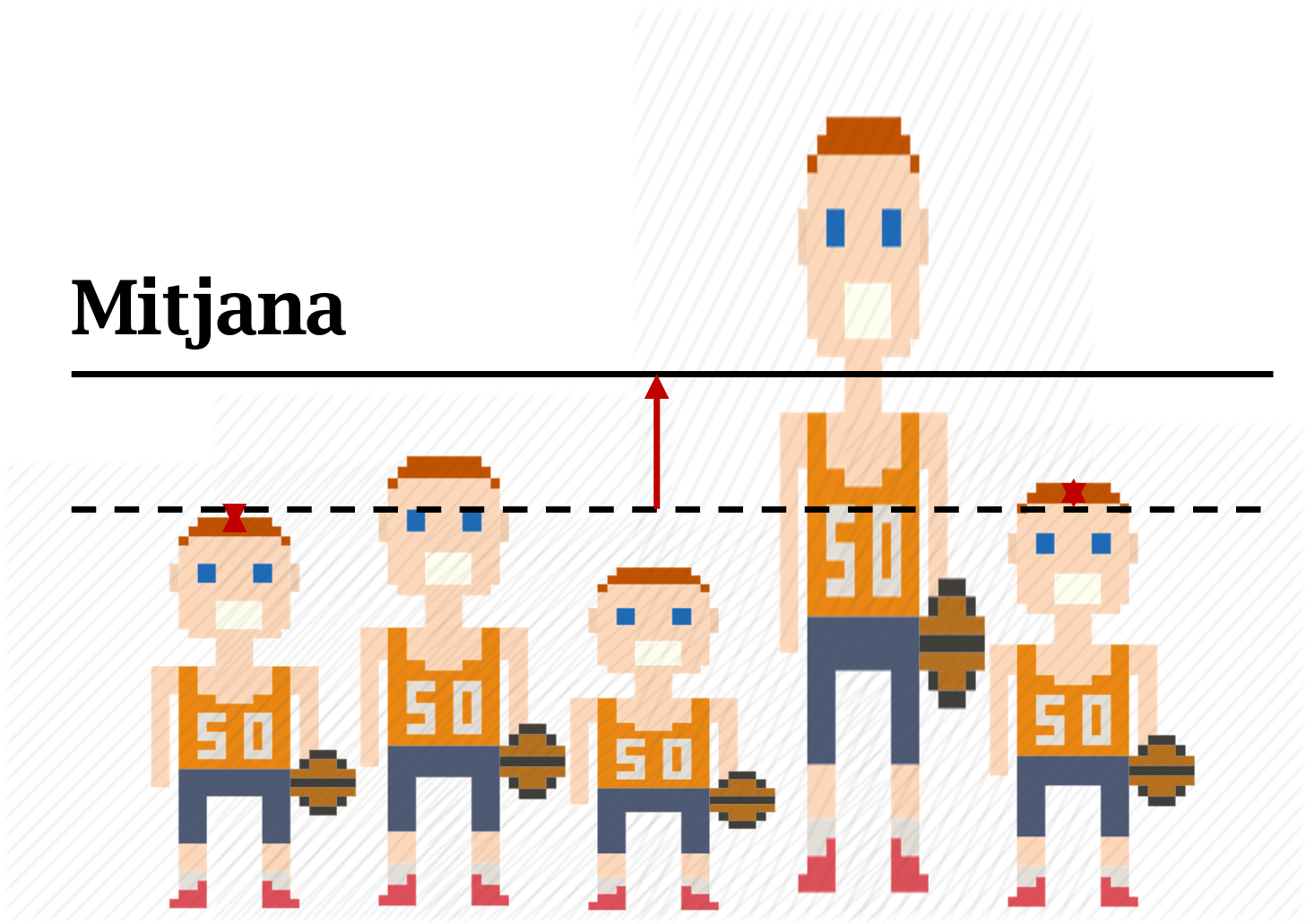
Como resumen de esta parte, es importante recordar que a menudo puede haber discrepancias sobre cuál es el “centro” de la distribución entre la moda, la media y la mediana. Esto nos indica que lo más importante será observar una distribución desde todos los puntos de vista para no quedarnos con una única impresión equivocada. Un ejemplo clásico de impresiones equivocadas lo encontramos en el recuadro siguiente (Las desigualdades: la media y la mediana).
En el periodo 1993-2013 el PIB per cápita de Estados Unidos creció un 40 %. Esta cifra se calcula a partir de la media de la renta. Esto significa que en 2013, si repartiéramos este crecimiento a partes iguales entre toda la ciudadanía norteamericana, todo el mundo habría ganado un 40 % más en relación con el dinero que ganaba en 1993. Sin embargo, la media puede ser que no refleje adecuadamente la forma en la que este crecimiento se ha trasladado a la mayoría de los hogares. Tenemos que pensar que la distribución de la renta acostumbra a tener una asimetría negativa, en la que hay una presencia de casos extremos (los superricos) en la parte superior de la distribución. Fijémonos en la imagen de la figura 8.8, publicada en 2013 por el New York Times con el título You Can’t Feed a Family With G.D.P, donde se observa la diferencia de crecimiento calculado con la media (PIB per cápita) y con la mediana.
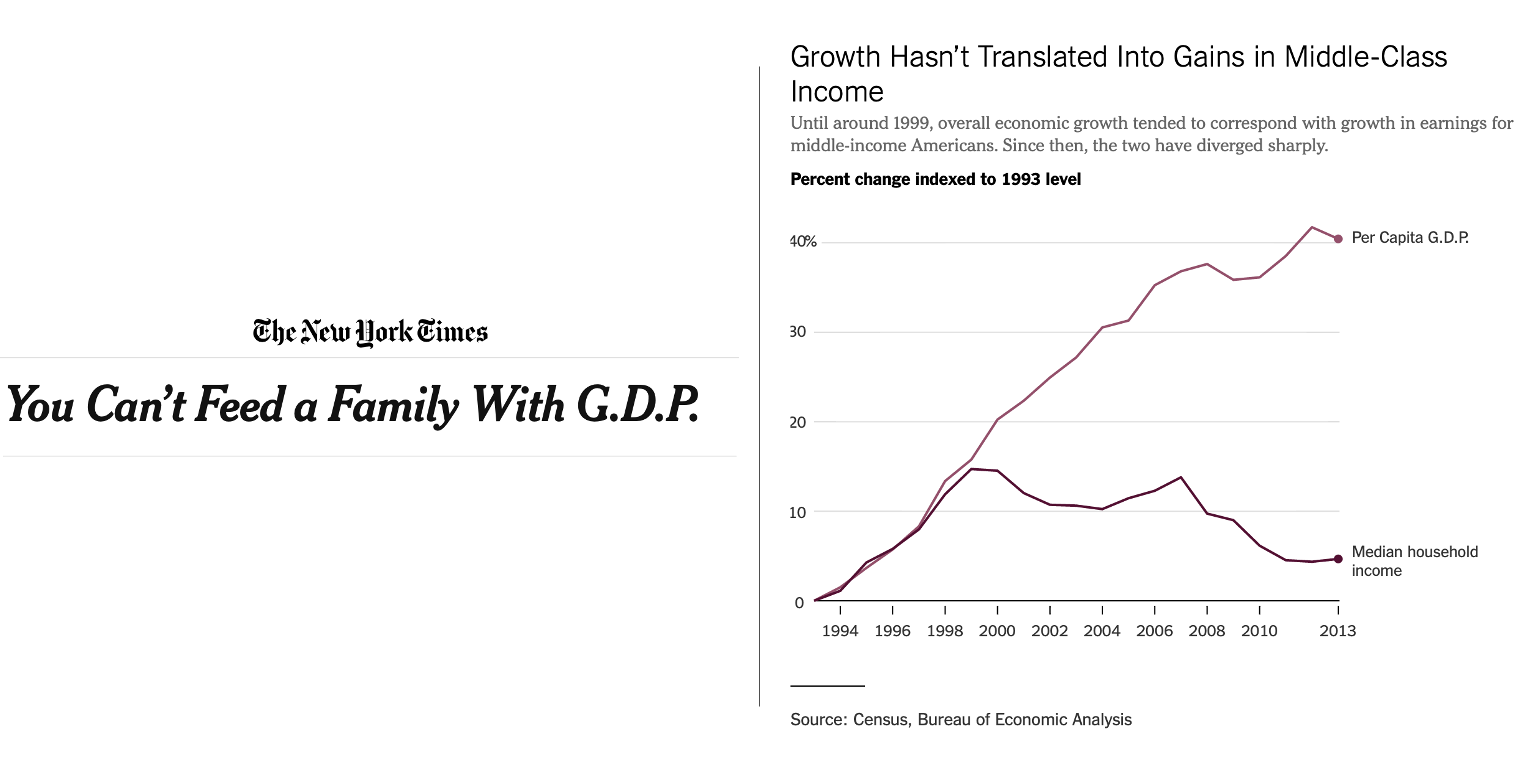
El gráfico nos muestra que las cosas no han ido todo lo bien que parece para el ciudadano americano mediano. Esta persona, que tiene la característica de ser más rica que el 50 % de la población y más pobre que el otro 50 %, ha visto como sus ingresos han crecido vagamente un 5 % a lo largo de dos décadas, descontando la inflación. Esto significa que el crecimiento económico de Estados Unidos ha sido sensible a casos extremos: grandes fortunas que han ganado mucho dinero, que han hecho subir la media de ingresos del país pero han mantenido casi inalterado el ingreso mediano.
8.3 Medidas de dispersión
Si hasta ahora nos hemos preocupado por buscar el centro, en este apartado nos dedicaremos a responder otra pregunta: ¿cuán dispersos están los números de una distribución? De nuevo, tendremos que encontrar algún procedimiento que nos permita resumir de forma cuantitativa o visual esta inquietud que tenemos. Las medidas de dispersión indican la variabilidad o la extensión de la distribución de los datos. Una dispersión alta indica que los datos están más extendidos, mientras que una dispersión baja indica que los datos están más concentrados. Hay tres preguntas principales que nos podemos hacer:
- ¿Cuál es la amplitud o el rango de los datos? Es decir, ¿cuál es la diferencia entre el valor mínimo y el valor máximo?
- Si ordenamos los valores de una distribución de más a menos, ¿cuál es la diferencia entre la observación situada en el 25 % y la observación situada en el 75 % de la distribución? El resultado se denomina rango intercuartílico.
- ¿Cuán dispersas están las observaciones en relación con el centro? El resultado es la desviación típica.
8.3.1 Amplitud
La amplitud o rango de la distribución es la diferencia entre el valor máximo y el valor mínimo de la variable (figura 8.9). Como ya sabéis, el valor máximo se calcula con la función max() y el valor mínimo con min(). Si buscamos qué amplitud tienen las alturas del equipo de baloncesto, la respuesta es 28.
Otra forma de calcular la amplitud de una variable es con la combinación de las funciones range() y diff(). La función range() nos devuelve un vector numérico con el mínimo y el máximo de la distribución, mientras que diff() nos calcula la diferencia entre estos dos valores.
8.3.2 Rango intercuartílico
Uno de los problemas de calcular la amplitud es que la cifra obtenida puede variar mucho o poco en función de si hay presencia de valores extremos. Podemos pensar que una distribución tiene mucha amplitud cuando la mayor parte de los valores están concentrados en un espacio muy pequeño y, en cambio, solo un valor está situado muy lejos del resto. Y con esto también nos podemos llevar una impresión equivocada de los datos.
Para evitar los casos extremos y obtener así una referencia aproximada de los datos entre sus valores más centrales, podemos calcular el rango intercuartílico, que mide la diferencia entre el primero y el tercer cuartil de la distribución. En otras palabras, mide la diferencia entre los valores que ocupan los lugares 25 y 75 % en una distribución ordenada (figura 8.10). Esta medida de dispersión se puede obtener con la función IQR() o la función quantile().
Veamos primero la función quantile(), que nos es útil para conocer cuál es el valor que ocupa una posición determinada en una distribución. En el código siguiente preguntamos cuál es la altura del jugador de bsk que ocupa el lugar 25 % de la distribución (el segundo más bajo) y cuál es la altura del que ocupa el lugar 75 % (el segundo más alto). Seguidamente, calculamos la diferencia entre estas alturas.
Una forma más rápida es con la función IQR(), que responde a InterQuartilic Range y nos hace el mismo cálculo.
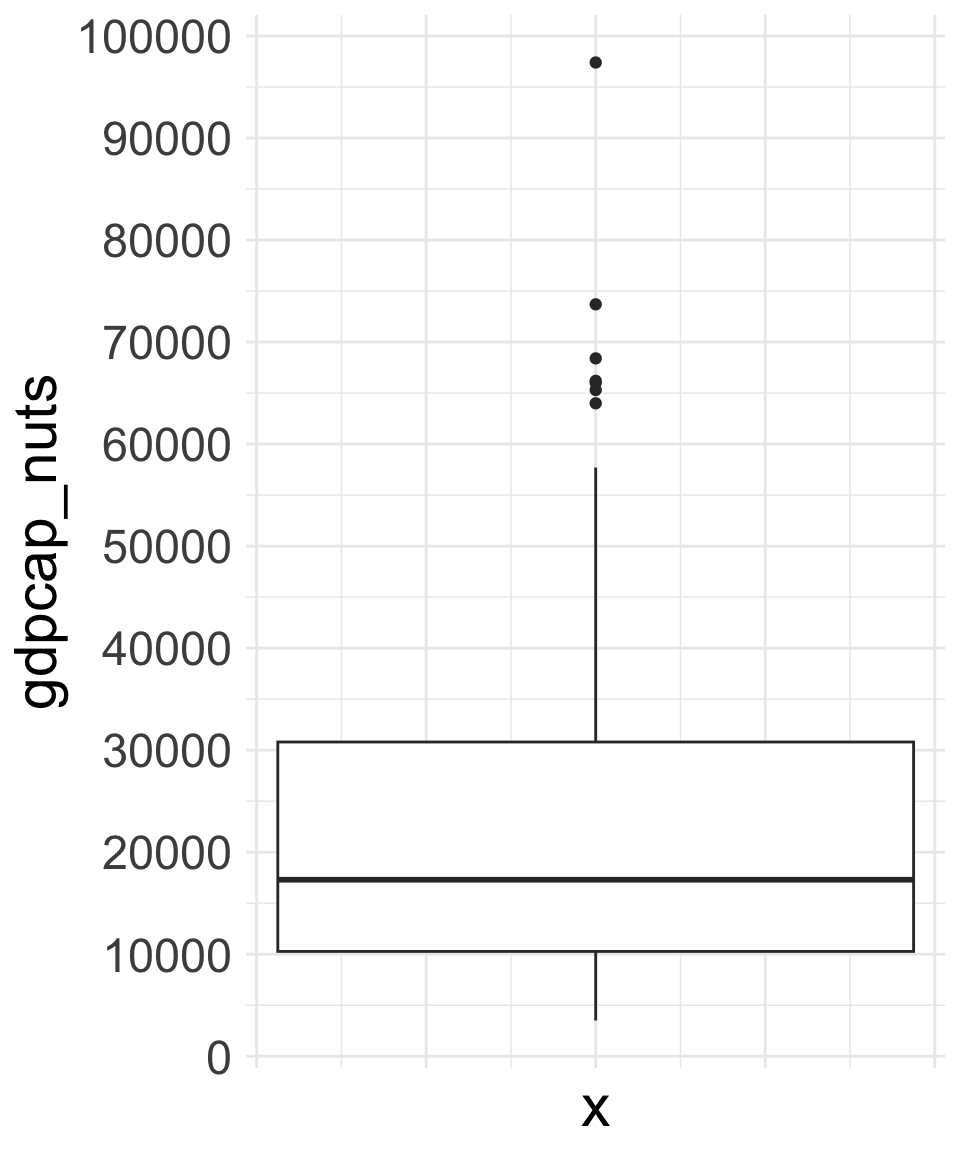
La caja tiene tres puntos de referencia: la línea más gruesa del medio es la mediana, que correspondería a la observación que ocupa el 50 % de la distribución, el extremo superior de la caja es el 75 % y el extremo inferior es el 25 %. La amplitud se encuentra representada por la línea vertical y los puntos. La línea vertical llega hasta el mínimo y el máximo de la distribución, y solo se convierte en un punto para indicar los casos extremos.
IQR(bsk)
## [1] 15Hay una visualización que nos permite ver con mucha claridad el rango intercuartílico de una distribución y su diferencia con la amplitud. Esta visualización es el diagrama de cajas, que observamos en la figura 8.11 del lateral junto con una descripción de cómo interpretar el gráfico. En el diagrama vemos representada la variable gdpcap_nuts. Los extremos superior e inferior de la caja corresponden al rango intercuartílico, por el cual podemos deducir que el valor 25 % se encuentra aproximadamente en el valor 10.000 y el valor 75 % se encuentra cerca de 30.000, y por eso el rango intercuartílico será aproximadamente de 20.000. La amplitud de la variable se encuentra aproximadamente entre los valores 2.000 y 100.000, y por eso podemos pensar que se acercará a 98.000. Fijaos que la presencia de un caso extremo hace que el valor máximo pase de 75.000 a 100.000, lo que ilustra que un solo caso puede hacer variar de forma importante la amplitud de los datos.
quantile(nuts$gdpcap_nuts, na.rm = T, 0.25)
## 25%
## 10275
quantile(nuts$gdpcap_nuts, na.rm = T, 0.75)
## 75%
## 30800
IQR(nuts$gdpcap_nuts, na.rm = T)
## [1] 20525
max(nuts$gdpcap_nuts, na.rm = T)
## [1] 97400
min(nuts$gdpcap_nuts, na.rm = T)
## [1] 3500
diff(range(nuts$gdpcap_nuts, na.rm = T))
## [1] 939008.3.3 Desviación típica o estándar
La desviación típica o desviación estándar es una medida de dispersión que nos ayuda a hacernos una idea de cuán separados están los valores de una variable en relación con una medida central, normalmente la media. Para intentar entender la lógica que sigue el cálculo de la desviación típica, veamos un ejemplo. En la figura 8.12, la imagen de la izquierda (a) muestra una distribución que ya conocemos: la del equipo de baloncesto que ha aparecido varias veces. La única novedad es que hemos incorporado unas flechas de color rojo que marcan la diferencia entre la altura de cada componente del equipo y la media. Ahora fijémonos en la imagen de la derecha. En relación con la primera imagen, en esta tenemos un jugador más bajito y dos jugadores más altos. Esto hace que la distancia de las alturas respecto a la media sea mayor en esta segunda imagen. La desviación típica, pues, será mayor en la imagen b que en la imagen a.
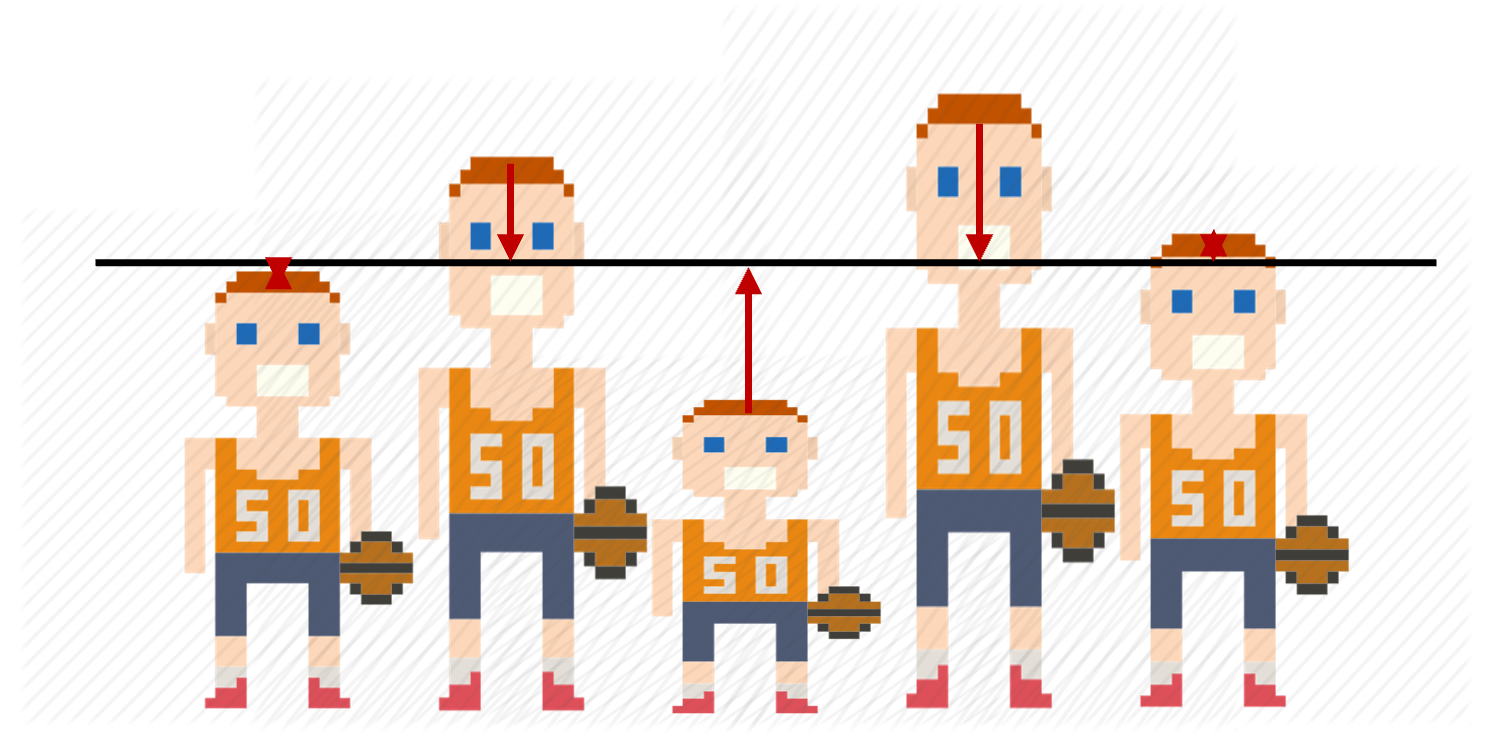
La fórmula de la desviación típica es bastante más compleja de lo que acabamos de explicar, pero, para entenderla de forma sencilla, el ejemplo anterior ilustra su lógica. En esencia, la desviación típica mide la dispersión media respecto de la media. Un valor alto querrá decir que los valores están situados lejos de la media, mientras que un valor bajo querrá decir que los valores están concentrados cerca de la media4.
4 Quien quiera saber cómo se calcula, puede seguir el ejercicio Calcular la desviación típica, que se encuentra más abajo en este módulo. Lo que sí es importante, sin embargo, es entender la lógica que hay detrás de esta medida.
Para calcular la desviación típica, utilizaremos la función sd(). Como ejemplo, reproduciremos numéricamente la figura anterior. Las alturas del gráfico a están guardadas en el objeto bsk_a y las del gráfico b en el objeto bsk_b. Fijémonos que la media es la misma en ambos casos, pero, como los valores están más lejos de la media en el segundo, la desviación típica es mayor en bsk_b.
¿Qué significan, sin embargo, las cifras 11.59 y 18.80? La desviación típica está medida con las mismas unidades que los valores originales. Por lo tanto, como los valores de los vectores bsk_a y bsk_b representan centímetros de altura, la desviación típica la podemos interpretar en centímetros. Aproximadamente, podemos interpretar que en el gráfico a los jugadores están 11.59 centímetros lejos de la media y en el gráfico b lo están 18.80. Este aspecto hay que tenerlo en cuenta, porque con la desviación típica solo podremos comparar distribuciones que estén medidas en las mismas unidades5.
5 Por ejemplo, no podríamos comparar ingreso mensual y años de edad. Los valores de ingreso mensual oscilan entre 1.000 y 100.000 euros, mientras que los años de edad lo hacen entre 0 y 80. Obviamente, habrá mucha más dispersión en el primer caso que no en el segundo. Sí que podremos comparar la desviación típica del ingreso mensual en dos poblaciones diferentes.
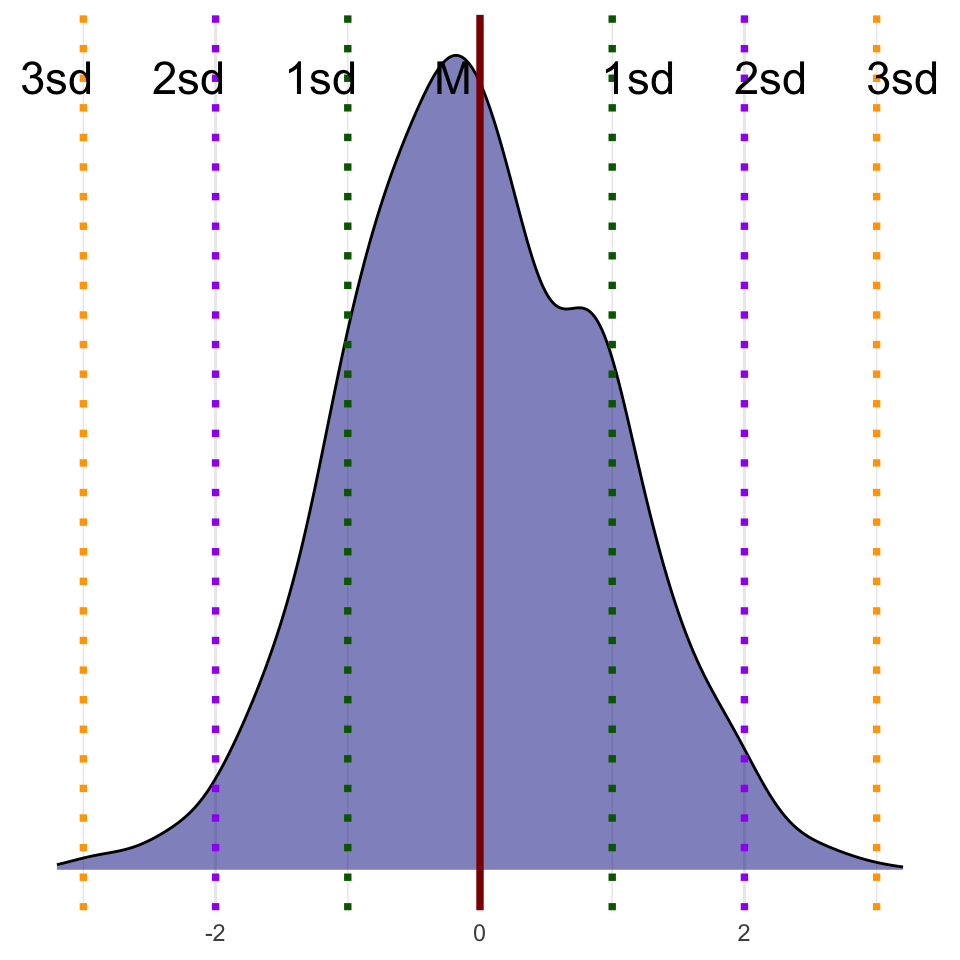
Finalmente, también es importante destacar que la desviación típica nos indica con bastante precisión qué porcentaje de valores están situados alrededor de la media. En una distribución normal (figura 8.13), una desviación típica nos indicará que el 68,2 % de los valores están situados a la izquierda y a la derecha de la media. Dos desviaciones típicas nos indicarán que un 95,4 % de los valores están situados a izquierda y derecha de la media y tres desviaciones típicas nos indicarán que el 99,6 de los valores están situados a izquierda y derecha de la media. Por lo tanto, asumiendo una determinada forma de la distribución, la desviación típica nos puede dar mucha información de cómo están repartidos los valores alrededor de la media.
Ejercicio 8.3 (¿Qué es exactamente la desviación típica?) En este ejercicio, ¿cómo se calcula exactamente la desviación típica? En primer lugar, creamos un marco de datos con dos vectores numéricos. Los dos vectores tienen la misma media.
En el gráfico siguiente podemos observar cuán lejos están los valores respecto de la media. En el vector vec2, los valores están, de media, más lejos de la media que en el vector vec1.
Para calcular la desviación típica, primero calculamos la distancia de cada valor respecto de la media. Utilizamos el vec1.
diff <- devs$vec1 - mean(devs$vec1)
diff
## [1] -3 1 -1 3En segundo lugar, elevamos las diferencias al cuadrado. Esto implica que dejamos de tener números negativos y que los valores que están lejos de la media pesarán más en el cómputo que los valores que están cerca.
sq_diff <- diff^2
sq_diff
## [1] 9 1 1 9A continuación, sumamos los valores del vector. El resultado de la suma lo dividimos por el número de casos menos uno. Este valor se denomina varianza, que es la media de las desviaciones cuadráticas respecto de la media.
La desviación típica es la raíz cuadrada de la varianza.
sqrt(variance)
## [1] 2.581989Ahora comprobamos que el resultado es el mismo que utilizando la función sd().
sd(devs$vec1)
## [1] 2.5819898.4 Medidas de localización
Las medidas de localización nos proporcionan información de la posición de un valor específico de la distribución respecto al resto de datos. Anteriormente, ya hemos visto algunas medidas que son consideradas de localización. La mediana, por ejemplo, nos proporciona el valor que divide la distribución ordenada en dos partes iguales, y este valor es el que se encuentra en su punto medio (50 %) del conjunto de datos. Además, utilizando cuartiles, hemos identificado dos valores clave: el cuartil 1 nos señala el punto en que se localiza el 25 % inferior de los datos, mientras que el cuartil 3 identifica el lugar donde se encuentra el 75 % superior de la distribución. Podemos agrupar las medidas de localización en tres categorías principales:
- Cuartiles. Dividen la distribución en cuatro segmentos de igual tamaño. El primer cuartil incluye los valores que incluyen desde el 0 % hasta el 25 % de la distribución, el segundo cuartil va del 25 % al 50 %, el tercer cuartil se refiere al segmento del 50 % al 75 %, y, finalmente, el cuarto cuartil cubre del 75 % al 100 %.
- Deciles. Dividen la distribución en diez segmentos de igual tamaño. El primer decil incluye los valores que van desde el 0 % hasta el 10 %, el segundo decil va del 10 % al 20 %, y así sucesivamente.
- Percentiles. Dividen la distribución en cien segmentos de igual tamaño. La lógica funciona igual que en los cuartiles y los deciles.
Para localizar la posición que ocupa un valor específico en la distribución, utilizaremos la función quantile(). En esta función indicaremos como primer argumento el vector en cuestión, seguido de la posición que queramos identificar, expresada en escala de 0 a 1. Finalmente, incluiremos como es habitual el argumento na.rm = T. En este ejemplo hemos buscado el percentil 45 % y el percentil 90 %.
El cero nos devolverá el valor más bajo y el 1 nos devolverá el valor más alto de la distribución.
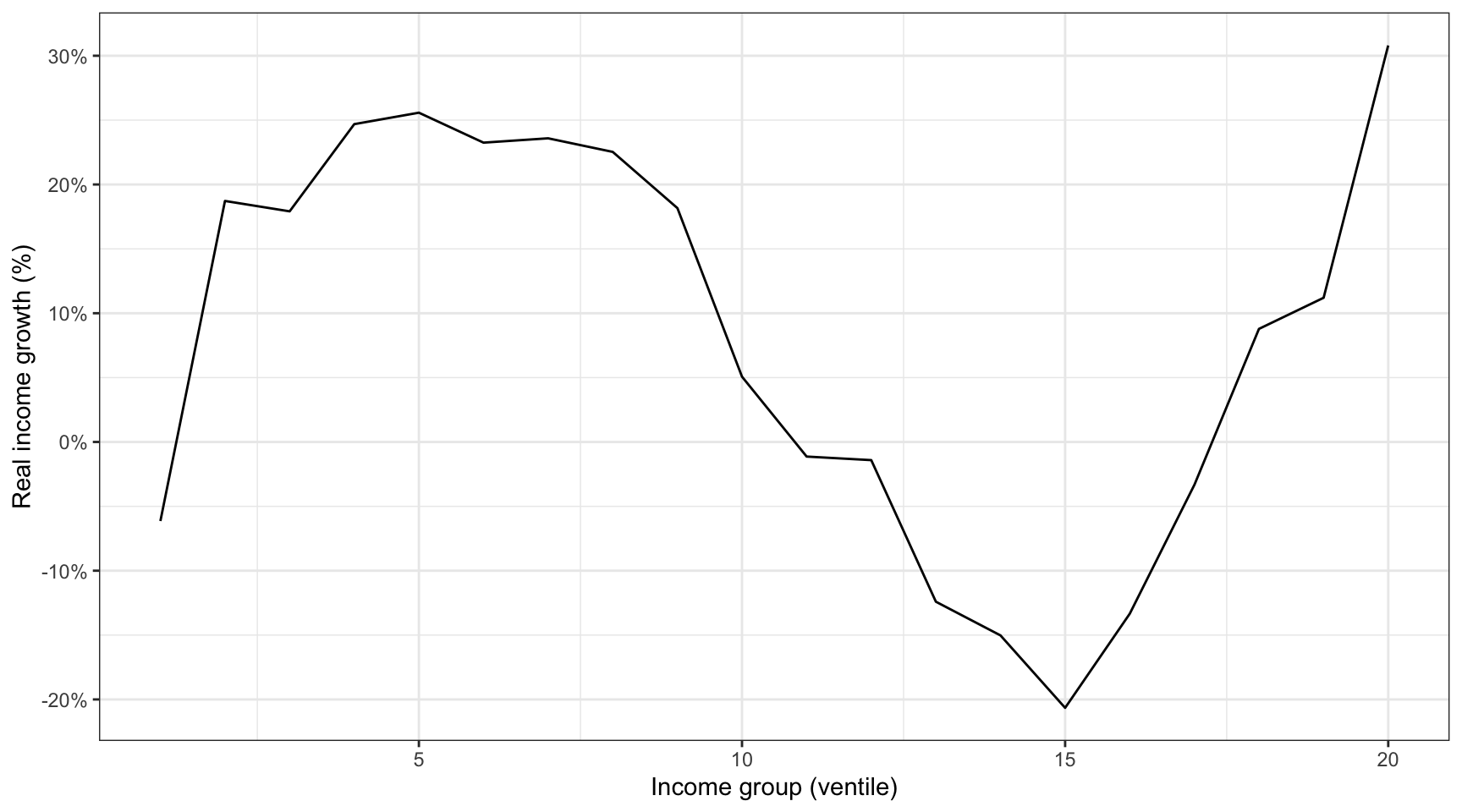
En los últimos años se han realizado muchos esfuerzos para medir la distribución de la renta tanto a escala global como por países. Uno de los estudios más populares en este aspecto lo elaboraron el economista del Banco Mundial Christoph Lakner y el académico Branko Milanovic, que calcularon la distribución de la renta por deciles de población en cada país del mundo en varios años (Lakner & Milanovic, 2013). Una vez tuvieron los datos por país, las agregaron a escala global en ventiles (20 segmentos de igual tamaño), lo que permitió observar la distribución de la renta a escala global.
El resultado más popular de este estudio se conoció como el elefante de Milanovic, que encontramos en la figura 8.14. Este gráfico muestra cómo ha variado la renta real de cada ventil de 1988 a 2008. El ventil más pobre de la población mundial (del 0 % al 5 %) se empobreció durante el periodo 1988-2008. En cambio, la renta real media de los grupos que comprenden del ventil 2 al ventil 10 aumentó considerablemente, cerca de un 20 %. El más beneficiado fue el grupo del ventil más alto, que experimentó un aumento de renta superior al 30 %.
Podéis descargar los datos y reproducir el elefante de Milanovic en este ejercicio.