1 El problema de les projeccions cartogràfiques
1.1 Introducció
Una projecció cartogràfica és qualsevol sistema o mètode utilitzat per transformar la representació cartogràfica de la superfície esferoidal de la Terra en una superfície plana. Quan volem representar l’esfera terrestre de manera plana, sempre ens trobarem amb el mateix problema: haurem d’establir un mètode per transformar la representació de l’esfera terrestre, de tres dimensions, en una superfície plana, de dues dimensions, ja que la representació d’una superfície esfèrica sobre una superfície plana mai no podrà ser totalment acurada (IGN 2020). Per comprendre millor aquesta idea, recomanem mirar el vídeo que trobareu a la dreta.
Així doncs, per representar la superfície de la Terra en dues dimensions haurem de distorsionar algun element de la mateixa. Tota projecció cartogràfica preservarà alguns aspectes a costa de distorsionar-ne d’altres. Els tres aspectes amb els quals podem jugar mitjançant una projecció són:
- La superfície dels elements representats.
- Les distàncies entre dos punts qualssevol.
- Els angles dels elements representats.
En base a aquests tres criteris, distingim principalment tres tipus de projeccions:
- Les projeccions equidistants preserven les proporcions entre les àrees representades. Tanmateix, això implica deformar bastant les formes i els angles.
- Les projeccions equivalents mantenen les distàncies respecte a un o més punts de referència del mapa.
- Les projeccions conformes conserven les formes (els angles).
A continuació, veurem com al llarg de la història s’han establert aquestes projeccions.
1.2 La projecció de Mercator
La projecció de Mercator és probablement la projecció més coneguda avui dia. Va ser calculada l’any 1569 pel matemàtic i cartògraf flamenc, Gerhard Kremer (Rupelmonde 1512 – Duisburg 1594), conegut pel seu nom llatinitzat de Gerardus Mercator. Si bé el propòsit de la projecció Mercator no era representar el nostre món, és el què al final ha acabat passant durant segles. Els motius pels quals aquesta projecció és tant coneguda els hem de buscar en la història i en la creixent importància del comerç marítim i dels països d’Occident.
1.2.1 El comerç marítim i nord global
Durant el segle XVI, la conquesta d’Àfrica i Amèrica per part de les potències colonials europees va donar lloc a una expansió sense precedents del comerç internacional. Aquesta expansió va ser impulsada principalment pel sistema de comerç triangular a través de l’oceà Atlàntic, que implicava el transport de mercaderies, passatgers i esclaus. A mesura que aquest sistema es desenvolupava, es va fer cada vegada més evident la necessitat de millorar les eines de navegació.
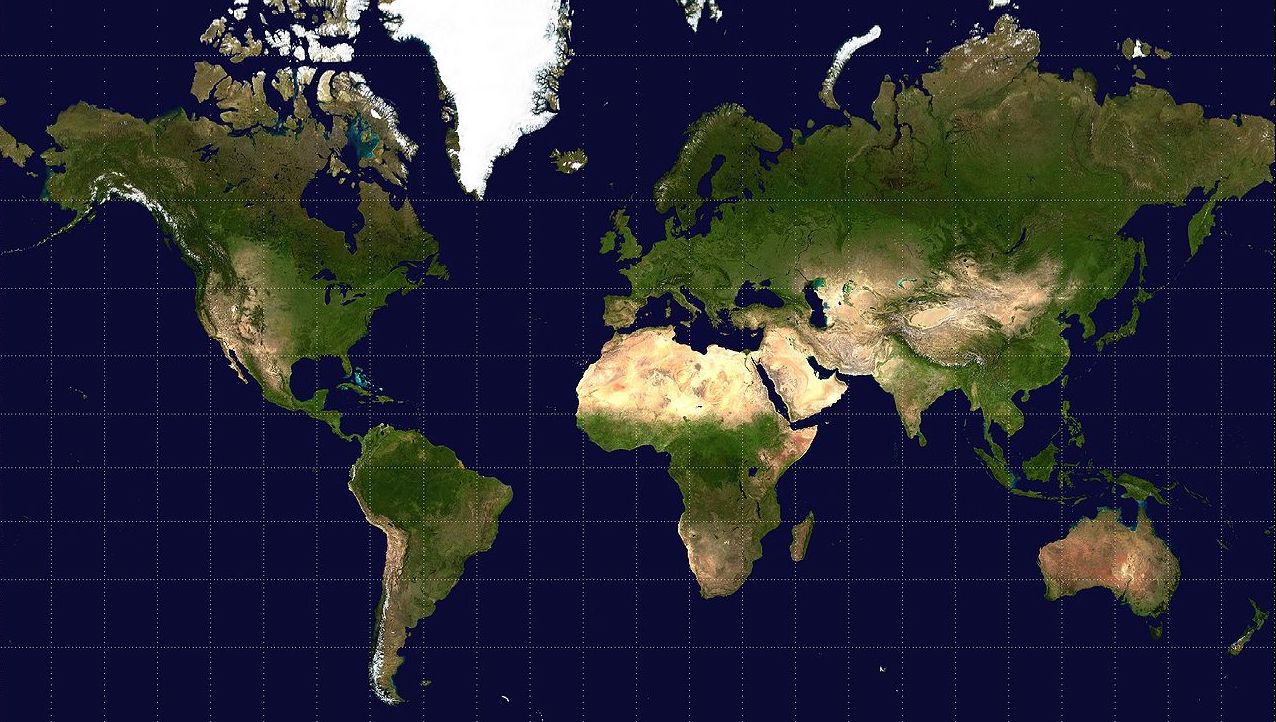
Una eina de navegació bàsica va ser l’anomenada projecció de Mercator. L’objectiu principal d’aquesta projecció era facilitar la navegació marítima, pel qual Mercator va representar el globus terrestre sobre una superfície cilíndrica, conservant els angles i les formes, però distorsionant l’àrea. Amb aquesta distorsió, Mercator aconseguia que les línies de rumb constant (línies que formen un angle constant amb els meridians) fossin representades amb segments rectes. És a dir, es pot traçar correctament el rumb de navegació com una recta, cosa que no succeeix sobre una superfície esfèrica.
Així, la projecció Mercator representa els meridians com a línies paral·leles entre si uniformement espaiades (equidistants), però té paral·lels desigualment espaiats, que estan més junts com més a prop estan de l’equador i són perpendiculars als meridians. Els pols Nord i Sud no es poden mostrar, l’escala és veritable al llarg de l’equador o al llarg de dos paral·lels equidistants de l’equador i es produeix una distorsió significativa de la grandària en les latituds més altes, i és per això que no es recomana utilitzar-la per a mapamundis.
Tal i com hem dit, la projecció Mercator, un estàndard per a cartes marítimes, es va definir per a les cartes de navegació i és en la navegació on més i millor s’utilitza (Lapaine and Usery 2015).
En resum, el gran inconvenient de la projecció de Mercator és que les àrees queden distorsionades a mesura que ens allunyem de l’equador. Hem de pensar que la línia de l’equador mesura en la realitat 40.000 km, mentre que els pols -nord i sud- són només un petit punt en una visió 3D de la Terra. Per tant, en la projecció Mercator tant els pols com l’equador estan representats amb la mateixa longitud. Per tant, a mesura que ens allunyem de l’equador estirem la Terra horitzontalment i, al mateix temps, també l’estirem verticalment per tal de mantenir la forma dels continents i els rumbs de navegació en línies rectes. En conseqüència, el que abans eren quadrats són ara rectangles, cada vegada més estirats, tal com podem observar a la figura 4.1.
Així doncs, a la projecció de Mercator els països o territoris propers als pols es visualitzaran molts més grans en relació a la seva mida real que no pas els països o territoris propers a l’equador. Per exemple, Àfrica té una superfície 15 vegades superior a Groenlàndia. En canvi, quan observem aquests dos territoris en una projecció de Mercator (figura 4.1), veiem que Groenlàndia i Àfrica tenen unes dimensions similars.
1.2.2 Mercator i el nord global
La manera com representem el món té conseqüències
Una de les implicacions que té i ha tingut la projecció de Mercator per les Relacions Internacionals i la Geopolítica és que l’anomenat nord global –Nord-Amèrica i Europa– està sobredimensionat en relació als territoris propers a l’equador, com l’Àfrica i Sud-Amèrica.
La projecció de Mercator va ser especialment emprada durant molts anys per les potències occidentals, ja que sobredimensionava la seva importància relativa envers altres països. Així, és comú veure episodis històrics com el domini de l’imperi britànic o la guerra freda representats mitjançant el mapa de Mercator. Aquesta projecció ha estat fortament criticada, en especial per països que estaven infrarrepresentats territorialment. Es diu que Mercator va coŀocar Europa al centre de mapa i desplaça la línia de l’equador cap avall, per motius ideològics, polítics, colonialistes o de poder (Aristasur 2020).
Altres versions del mapa de Mercator mostren visions de poder, com ara els que utilitzen la projecció de Mercator, eliminant la part més septentrional del mapa. El motiu estètic és que per sota de la latitud 55ºS no hi ha terra, excepte l’Antàrtida, que apareix deformada en la projecció de Mercator (Aristasur 2020). També en alguns casos s’ha fet servir per consideracions polítiques, ja que els països de l’hemisferi nord queden situats al centre del mapa.
El problema, doncs, no és la projecció, sinó l’ús polític que se’n fa. La política –els mapes són política i poder– sorgeix quan una projecció és assumida com a universal i unívoca, amb objectius que van molt més enllà per als quals havia estat creada. Els usos polítics de les projeccions cartogràfiques i els mapes són infinits.
El geògraf francès Yves Lacoste en parla àmpliament en el seu llibre La geografia: una arma per a la guerra (1976).
1.2.3 Universal Transversal Mercator
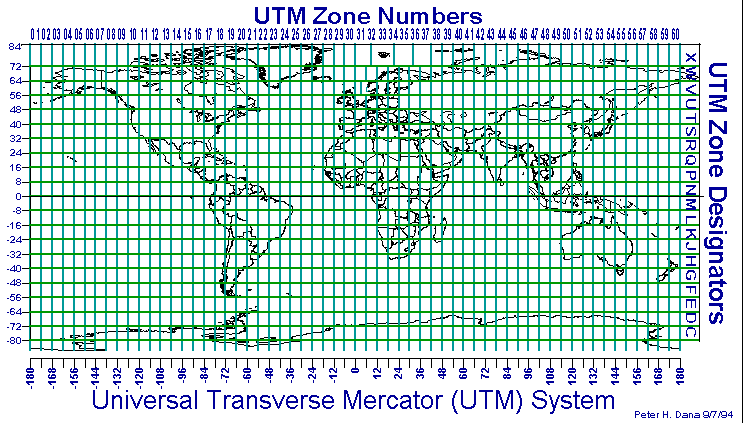
De la projecció Mercator en deriva la Universal Transversal Mercator (UTM), que es tracta d’una projecció cilíndrica millorada, àmpliament utilitzada als sistemes de coordenades de referència actuals (Rabella 2013).
La projecció transversa de Mercator, també coneguda com a projecció de Gauss-Krüger, és una projecció on la línia en que l’escala és constant es tracta d’un meridià, en comptes de la línia equatorial. El meridià central i l’equador són línies rectes. Altres meridians i paral·lels són corbes complexes i són còncaves cap al meridià central. La projecció té escala veritable al llarg del meridià central o al llarg de dues línies equidistants i paral·leles a ell. Generalment s’utilitza per a presentacions de petites àrees a gran escala. A causa de la distribució de la distorsió, s’utilitza generalment dividint la regió a cartografiar en zones de tres o de sis graus, limitades per meridians. Aquesta projecció s’utilitza sovint per a mapes topogràfics a escales 1:25.000 a 1:250.000, i és la base del sistema de coordenades UTM.
1.3 Mapa de Peters
Altres cartògrafs han desenvolupat projeccions alternatives a la projecció Mercator amb l’objectiu de compensar les crítiques sobre el seu presumpte eurocentrisme. Una d’aquestes projeccions és el mapa de Peters, que apareix en el marc dels primers corrents contestataris de l’ordre internacional durant les dècades de 1960 i 1970.
El mapa de Gall-Peters parteix també d’una projecció cilíndrica equidistant, però amb l’objectiu de mantenir les proporcions en les àrees (Rabella 2013). Així, doncs, Peters augmenta l’escala vertical de les regions properes a l’equador per compensar l’estirament en horitzontal de les regions temperades. Però crea així greus problemes de deformació a l’Àfrica i Sud-Amèrica. No obstant això, aquest mapa no serveix per navegar, ni per calcular distàncies entre dos punts. Per entendre millor el context històric del mapa de Peters, cal comprendre el teló de fons del debat cartogràfic que va existir durant el segle XX. Tradicionalment, la majoria dels mapes mundials utilitzaven la projecció de Mercator, desenvolupada per Gerardus Mercator al segle XVI. Aquesta projecció era útil per a la navegació i la representació de línies rectes de rumb constant, però tenia la desavantatge de distorsionar significativament les àrees de les terres properes als pols.
A mesura que es desenvolupava el moviment per la descolonització i la globalització, van sorgir crítiques a la projecció de Mercator. Es va argumentar que aquesta projecció dóna una visió eurocèntrica del món, ja que afavoreix els països de latituds més altes, com Europa i Amèrica del Nord, en detriment de les regions equatorials i del sud global.
És en aquest context que Arno Peters va presentar el seu mapa el 1974, conegut com la “Projecció de Peters” (figura 4.3), la qual buscava abordar la distorsió de la projecció de Mercator. El mapa de Peters presenta les àrees de manera més precisa, especialment per als països equatorials i del sud, però sacrifica la forma i la continuïtat direccional.
El mapa de Peters va generar controvèrsia i debat, i molts cartògrafs, geògrafs i experts en representació geogràfica han defensat i criticat diverses projeccions cartogràfiques al llarg dels anys. Alguns veuen el mapa de Peters com un intent de corregir la injustícia en la representació del món, mentre que d’altres consideren que hi ha altres projeccions més equitatives. El debat sobre la millor representació cartogràfica continua fins a avui dia, i hi ha una gran varietat de projeccions disponibles que s’ajusten a diferents propòsits i perspectives.
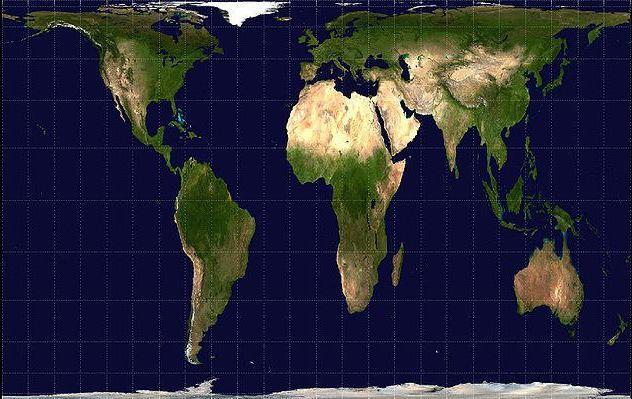
En definitiva, el mapa de Mercator no és perfecte, tampoc ho és el mapa de Peters. Ambdues són projeccions possibles de les moltes possibles que hi ha. Com afirmà Arthur Robinson, una projecció no és ni bona ni dolenta; només poden resultar encertades o desencertades les eleccions que en podem fer en relació amb un determinat tema o propòsit (Rabella 2013).
1.4 Winkel-Tripel
La projecció de Winkel Tripel, presentada per Oswald Winkel a Alemanya el 1921, està entremig d’una projecció conforme i una projecció equivalent.
La projecció s’obté fent una mitjana de les coordenades de les projeccions Equidistant Cilíndrica i Aitoff. Winkel afegeix el nom «Tripel», que normalment significa triple, perquè la projecció Aitoff posseeix un punt de vista equatorial d’un hemisferi de la projecció Equidistant Azimutal, en la qual les coordenades horitzontals s’han duplicat i als meridians se’ls han donat dues vegades les seves longituds originals.
El meridià central és recte. Els altres meridians són corbs, igualment espaiats al llarg de l’equador i còncaus cap al meridià central. L’equador i els pols són rectes. Els altres paral·lels són corbs, igualment espaiats al llarg del meridià central i còncaus cap al Pol més pròxim. Els pols són línies rectes al voltant de 0,4 vegades l’equador, en funció de la latitud dels paral·lels estàndard. L’escala és veritable al llarg del meridià central i constant al llarg de l’equador.
Com s’observa a la figura 4.4, la distorsió és moderada, excepte prop dels meridians exteriors de les regions polars. El Winkel Tripel s’utilitza per als mapes que incloguin a tot el món i és l’acceptada actualment per la National Geographic Society (NGS).
1.5 Cònica conforme de Lambert
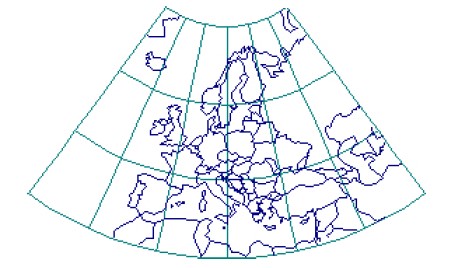
La projecció cònica conforme de Lambert (CCL), presentada per Johann Heinrich Lambert el 1772 (figura 4.5), mostra els meridians com a línies rectes equidistants que convergeixen en un dels pols. Els angles entre els meridians en la projecció són més petits que els angles corresponents al globus. Els paral·lels són arcs circulars concèntrics desigualment espaiats i centrats en el Pol, de tal forma que l’espaiament entre els paral·lels augmenta segons s’allunyen del pol. El pol més pròxim al paral·lel estàndard és un punt i l’altre pol no es pot mostrar. L’escala és veritable al llarg del paral·lel estàndard o al llarg de dos paral·lels estàndard, i és constant al llarg de qualsevol paral·lel determinat. La projecció cònica conforme de Lambert s’utilitza àmpliament per a la cartografia a gran escala de les regions amb un eix Est-Oest pronunciat i en regions de latitud mitjana. És habitual en molts països per a mapes a escala 1:500.000, així com per a les cartes aeronàutiques a una escala similar.
1.5.1 Projecció cilíndrica equivalent de Lambert
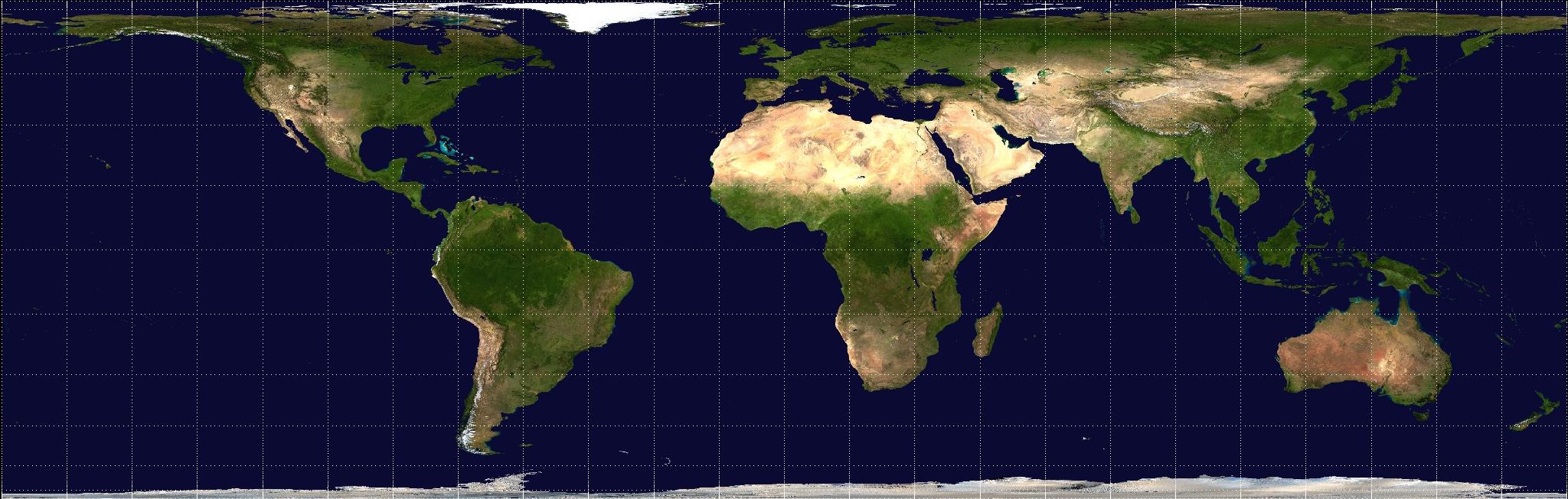
La projecció cilíndrica equivalent (d’àrees equivalents) va ser presentada per primera vegada per Johann Heinrich Lambert el 1772 i es va convertir en la base per a moltes altres projeccions equivalents similars, incloent-hi la Gall, la Behrmann, i les projeccions Trystan-Edwards (figura 4.6). La projecció original de Lambert utilitza una sola línia d’escala constant al llarg de la línia de l’equador. S’elaboren projeccions equivalents similars utilitzant dos paral·lels com les línies d’escala constant. En la projecció cilíndrica equivalent de Lambert, els meridians són línies rectes paral·leles i equidistants, i l’equador és π vegades més llarg que els meridians. Les línies de latitud són línies paral·leles desigualment espaiades, més allunyades com més prop de l’equador, i perpendiculars als meridians. Canviar l’espaiament dels paral·lels és el mètode utilitzat per a preservar àrees iguals. No obstant això, les importants distorsions de distàncies i angles donen lloc a una distorsió major en latituds altes prop dels pols. Aquesta projecció sovint no s’utilitza directament per a l’elaboració de mapes, però suposa un estàndard per a descriure els principis de les projeccions cartogràfiques en llibres de text, i també ha servit com a prototip per a altres projeccions.
Qui vulgui aprofundir aspectes més tècnics de la cartografia, pot consultar el següent llibre: Santamaría Peña, J. (2011). La Cartografía y las proyecciones cartográficas. Ingenierías, 15. Universidad de La Rioja.
1.6 Investigació sobre noves projeccions de mapes
El 2007, inspirats pel mètode de Robinson, B. Jenny, T. Patterson i L. Hurni van produir el programa interactiu Flex Projector, que permet a l’usuari crear noves projeccions de mapes del món amb facilitat. És compatible amb el punt de vista normal de les projeccions cilíndriques. El programa és gratuït, de fonts obertes, i funciona a Linux, Mac US X i Windows. A l’executar el programa, apareix a la pantalla un mapamundi a la projecció de Robinson (vegeu la figura 4.7).
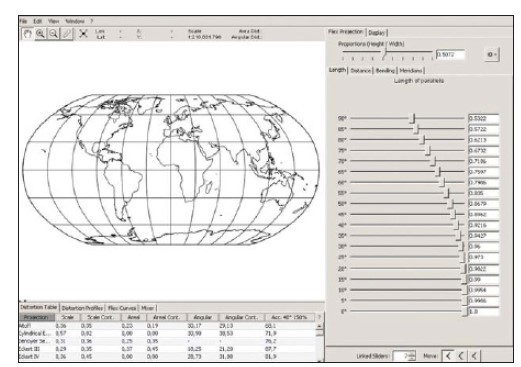
L’objectiu d’aquesta recerca és desenvolupar una alternativa a la projecció Web Mercator per als mapes a la web a petita escala, on els mapes utilitzen automàticament una projecció òptima en funció de l’escala del mapa, la seva relació altura-amplària i la latitud central de l’àrea mostrada.
1.7 Conclusions
La raó per la qual tenim tantes projeccions cartogràfiques és perquè cap funciona perfectament per a tot. La selecció d’una projecció cartogràfica apropiada per a una determinada aplicació depèn de diversos factors, incloent-hi el propòsit del mapa, el tipus de dades que es vol representar, la regió del món on es projecta i l’escala final del mapa. En els SIG, les bases de dades a gran escala (per a àrees petites) s’utilitzen projeccions conformes per a preservar els angles. Per a aquestes aplicacions, la distorsió d’àrees és tan petita sobre l’extensió geogràfica, que és insignificant i no és necessari l’ús d’una projecció que conservi àrees. Habitualment, els arxius de dades a gran escala s’utilitzen en aplicacions SIG d’extensió geogràfica limitada (per exemple, un comtat o un estat). Les dues projeccions més utilitzades per a aquestes escales, són la cònica conforme de Lambert i la transversal de Mercator, que són la base de la UTM i de la major part del sistema de coordenades del «USA State Plane». Per a mapamundis de consulta general, es recomana no utilitzar qualsevol projecció cilíndrica, sinó una pseudocilíndrica (per exemple, la de Robinson o una projecció de compromís com la de Winkel-Tripel).
En resum, les projeccions cartogràfiques i les transformacions de coordenades són la base de la consecució d’un marc comú de referència per a la informació geogràfica. El requisit de tenir un el·lipsoide, dàtum, projecció cartogràfica i finalment d’un sistema de coordenades planes, tots ells comuns, fan possible l’ús de la geometria plana per a tota mena de superposicions i anàlisis espacials. La projecció de les dades geogràfiques de la Terra el·lipsoidal sobre un sistema de coordenades planes, sempre es tradueix en una distorsió de les superfícies, formes, distàncies i altres propietats. Amb la selecció apropiada d’una projecció, l’usuari pot conservar les característiques desitjades a costa d’unes altres i mostrar la projecció geogràfica desitjada amb major precisió.