4 El problema de las proyecciones cartográficas
4.1 Introducción
Una proyección cartográfica es cualquier sistema o método utilizado para transformar la representación cartográfica de la superficie esferoidal de la Tierra en una superficie plana. Cuando queremos representar la esfera terrestre de manera plana, siempre nos encontraremos con el mismo problema: tendremos que establecer un método para transformar la representación de la esfera terrestre, de tres dimensiones (3D), en una superficie plana, de dos dimensiones (2D), puesto que la representación de una superficie esférica sobre una superficie plana nunca podrá ser totalmente fidedigna (IGN 2020). Para comprender mejor esta idea, recomendamos mirar el vídeo que encontraréis a la derecha.
Así pues, para representar la superficie de la Tierra en 2D tendremos que distorsionar algún elemento. Toda proyección cartográfica preservará algunos aspectos a expensas de distorsionar otros. Los tres aspectos con los cuales podemos jugar mediante una proyección son:
- La superficie de los elementos representados.
- Las distancias entre dos puntos cualesquiera.
- Los ángulos de los elementos representados.
Basándonos en estos tres criterios, distinguimos principalmente tres tipos de proyecciones:
- Las proyecciones equidistantes, que preservan las proporciones entre las áreas representadas. Aun así, esto implica deformar bastante las formas y los ángulos.
- Las proyecciones equivalentes, que mantienen las distancias respecto a uno o más puntos de referencia del mapa.
- Las proyecciones conformes, que conservan las formas (los ángulos).
A continuación, veremos cómo se han establecido estas proyecciones a lo largo de la historia.
4.2 La proyección de Mercator
La proyección de Mercator es probablemente la proyección más conocida hoy en día. Fue calculada en 1569 por el matemático y cartógrafo flamenco Gerhard Kremer (Rupelmonde, 1512 - Duisburgo, 1594), conocido por el nombre latinizado de Gerardus Mercator. Si bien el propósito de la proyección de Mercator no era representar nuestro mundo, es lo que al final ha acabado pasando durante siglos. Los motivos por los cuales esta proyección es tan conocida los tenemos que buscar en la historia y en la creciente importancia del comercio marítimo y de los países de Occidente.
4.2.1 El comercio marítimo y norte global
Durante el siglo XVI, la conquista de África y América por parte de las potencias coloniales europeas dio lugar a una expansión sin precedentes del comercio internacional. Esta expansión fue impulsada principalmente por el sistema de comercio triangular a través del océano Atlántico, que implicaba el transporte de mercancías, pasajeros y esclavos. A medida que este sistema se desarrollaba, se hizo cada vez más evidente la necesidad de mejorar las herramientas de navegación.
Una herramienta de navegación básica fue la llamada proyección de Mercator. El objetivo principal de esta proyección era facilitar la navegación marítima y por eso Mercator representó el globo terrestre sobre una superficie cilíndrica, conservando los ángulos y las formas pero distorsionando el área. Con esta distorsión, Mercator conseguía que las líneas de rumbo constante (líneas que forman un ángulo constante con los meridianos) fueran representadas con segmentos rectos. Es decir, se puede trazar correctamente el rumbo de navegación como una recta, cosa que no sucede sobre una superficie esférica.
Así, la proyección de Mercator representa los meridianos como líneas paralelas entre sí espaciadas uniformemente (equidistantes), pero tiene paralelos espaciados desigualmente, que están más juntos cuanto más cerca están del ecuador y son perpendiculares a los meridianos. Los polos Norte y Sur no se pueden mostrar, la escala es verdadera a lo largo del ecuador o a lo largo de dos paralelos equidistantes del ecuador, y se produce una distorsión significativa del tamaño en las latitudes más altas, y es por eso que no se recomienda utilizarla para mapamundis.
Tal como hemos dicho, la proyección de Mercator, un estándar para cartas marítimas, se definió para las cartas de navegación y es en la navegación donde se utiliza más y mejor (Lapaine and Usery 2015).
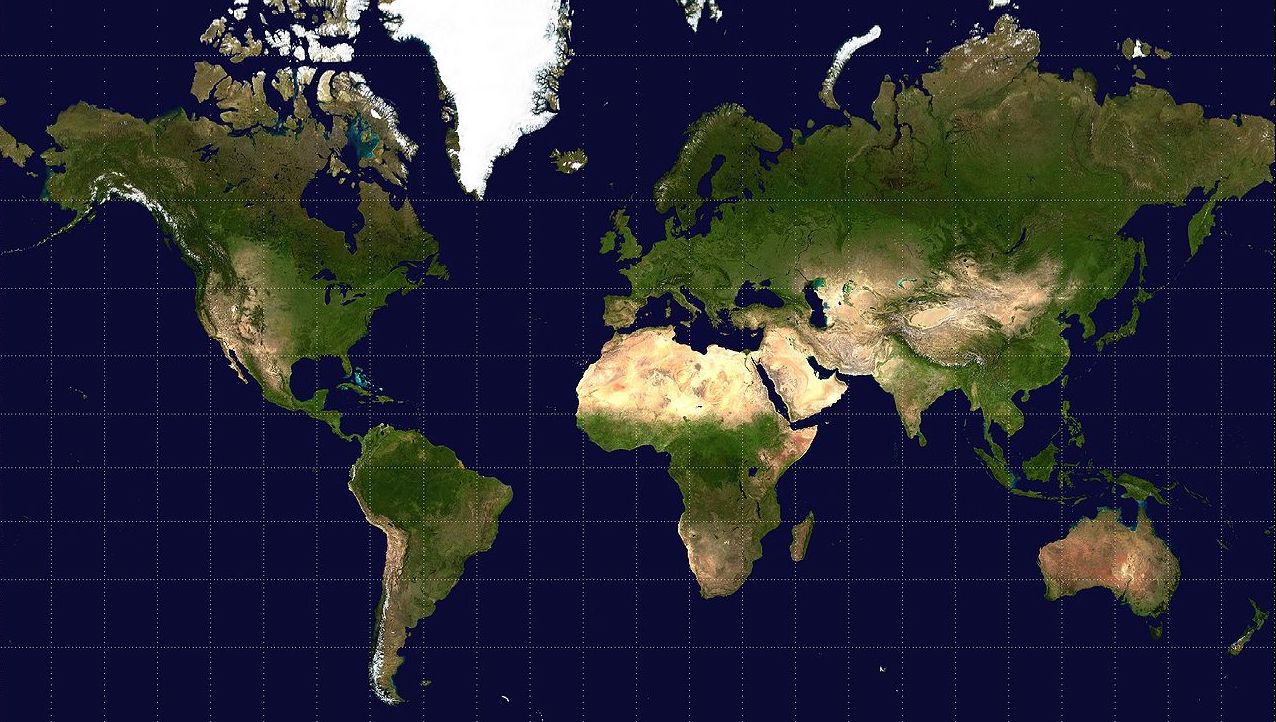
En resumen, el gran inconveniente de la proyección de Mercator es que las áreas quedan distorsionadas a medida que nos alejamos del ecuador. Tenemos que pensar que la línea del ecuador mide en la realidad 40.000 kilómetros, mientras que los polos (Norte y Sur) son solo un pequeño punto en una visión 3D de la Tierra. Por lo tanto, en la proyección de Mercator tanto los polos como el ecuador están representados con la misma longitud. Así pues, a medida que nos alejamos del ecuador, estiramos la Tierra horizontalmente y, al mismo tiempo, también la estiramos verticalmente para mantener la forma de los continentes y los rumbos de navegación en líneas rectas. En consecuencia, lo que antes eran cuadrados ahora son rectángulos cada vez más estirados, tal como podemos observar en la figura 4.1.
Así pues, en la proyección de Mercator los países o territorios próximos a los polos se visualizarán mucho más grandes en relación con su medida real que los países o territorios próximos al ecuador. Por ejemplo, África tiene una superficie quince veces superior a Groenlandia. En cambio, cuando observamos estos dos territorios en una proyección de Mercator (figura 4.1), vemos que Groenlandia y África tienen unas dimensiones similares.
4.2.2 Mercator y el norte global
La manera como representamos el mundo tiene consecuencias
Una de las implicaciones que tiene y ha tenido la proyección de Mercator en las Relaciones Internacionales y la Geopolítica es que el llamado norte global (Norteamérica y Europa) está sobredimensionado en relación con los territorios próximos al ecuador, como África y Sudamérica.
La proyección de Mercator fue empleada especialmente durante muchos años por las potencias occidentales, puesto que sobredimensionaba su importancia relativa respecto a otros países. Así, es común ver episodios históricos como el dominio del Imperio británico o la Guerra Fría representados mediante el mapa de Mercator. Esta proyección ha sido fuertemente criticada, en especial por países que estaban infrarrepresentados territorialmente. Se dice que Mercator colocó Europa en el centro del mapa y desplazó la línea del ecuador hacia abajo por motivos ideológicos, políticos, colonialistas o de poder (Aristasur 2020).
Otras versiones del mapa de Mercator muestran visiones de poder, como por ejemplo las que utilizan la proyección de Mercator eliminando la parte más septentrional del mapa. El motivo estético es que por debajo de la latitud 55° S no hay tierra, excepto la Antártida, que aparece deformada en la proyección de Mercator (Aristasur 2020). También en algunos casos se ha usado por consideraciones políticas, puesto que los países del hemisferio norte quedan situados en el centro del mapa.
El problema, pues, no es la proyección, sino el uso político que se hace. La política —los mapas son política y poder— surge cuando una proyección es asumida como universal y unívoca, con objetivos que van mucho más allá para los cuales había sido creada. Los usos políticos de las proyecciones cartográficas y los mapas son infinitos.
El geógrafo francés Yves Lacoste habla ampliamente en su libro La geografía: un arma para la guerra (1976).
4.2.3 Universal Transversal Mercator
De la proyección de Mercator deriva la Universal Transversal Mercator (UTM), que se trata de una proyección cilíndrica mejorada, utilizada ampliamente en los sistemas de coordenadas de referencia actuales (Rabella 2013).
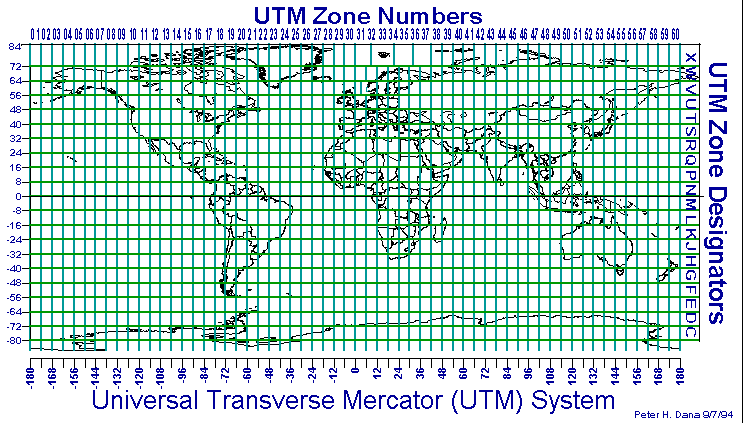
La proyección transversa de Mercator, conocida también como proyección de Gauss-Krüger, es una proyección en que la línea en la que la escala es constante es un meridiano en vez de la línea ecuatorial. El meridiano central y el ecuador son líneas rectas. Otros meridianos y paralelos son curvas complejas y son cóncavas hacia el meridiano central. La proyección tiene escala verdadera a lo largo del meridiano central o a lo largo de dos líneas equidistantes y paralelas a él. Generalmente, se utiliza para presentaciones de pequeñas áreas a gran escala. A causa de la distribución de la distorsión, se utiliza generalmente dividiendo la región a cartografiar en zonas de tres o seis grados limitadas por meridianos. Esta proyección se utiliza a menudo para mapas topográficos a escalas entre 1:25.000 y 1:250.000, y es la base del sistema de coordenadas UTM.
4.3 Mapa de Peters
Otros cartógrafos han desarrollado proyecciones alternativas a la proyección de Mercator con el objetivo de compensar las críticas sobre su presunto eurocentrismo. Una de estas proyecciones es el mapa de Peters, que aparece en el marco de las primeras corrientes contestatarias del orden internacional durante las décadas del 1960 y del 1970.
El mapa de Gall-Peters parte también de una proyección cilíndrica equidistante, pero con el objetivo de mantener las proporciones en las áreas (Rabella 2013). Así pues, Peters aumenta la escala vertical de las regiones próximas al ecuador para compensar el estiramiento en horizontal de las regiones templadas. Pero así crea graves problemas de deformación en África y Sudamérica. Sin embargo, este mapa no sirve para navegar ni para calcular distancias entre dos puntos. Para entender mejor el contexto histórico del mapa de Peters, hay que comprender el telón de fondo del debate cartográfico que existió durante el siglo XX. Tradicionalmente, la mayoría de los mapas mundiales utilizaban la proyección de Mercator desarrollada por Gerardus Mercator en el siglo XVI. Esta proyección era útil para la navegación y la representación de líneas rectas de rumbo constante, pero tenía la desventaja de distorsionar significativamente las áreas de las tierras próximas a los polos.
A medida que se desarrollaba el movimiento por la descolonización y la globalización, surgieron críticas a la proyección de Mercator. Se argumentó que esta proyección da una visión eurocéntrica del mundo, puesto que favorece a los países de latitudes más altas, como Europa y Norteamérica, en detrimento de las regiones ecuatoriales y del sur global.
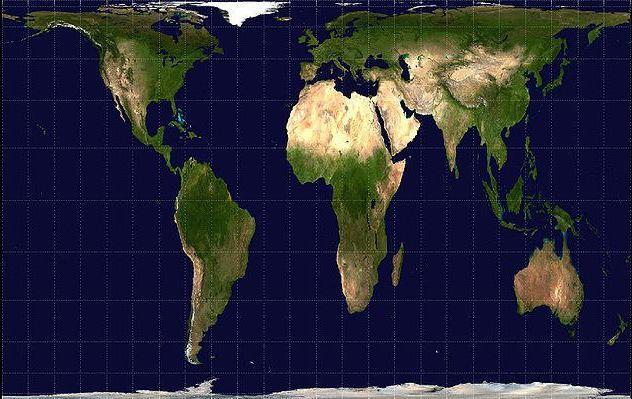
Es en este contexto que en 1974 Arno Peters presentó su mapa, conocido como la “proyección de Peters” (figura 4.3), que buscaba abordar la distorsión de la proyección de Mercator. El mapa de Peters presenta las áreas de manera más precisa, especialmente para los países ecuatoriales y del sur, pero sacrifica la forma y la continuidad direccional.
El mapa de Peters generó controversia y debate, y muchos cartógrafos, geógrafos y expertos en representación geográfica han defendido y criticado varias proyecciones cartográficas a lo largo de los años. Algunos ven el mapa de Peters como un intento de corregir la injusticia en la representación del mundo, mientras que otros consideran que hay otras proyecciones más equitativas. El debate sobre la mejor representación cartográfica continúa hasta hoy día, y hay una gran variedad de proyecciones disponibles que se ajustan a diferentes propósitos y perspectivas.
En definitiva, el mapa de Mercator no es perfecto, y tampoco lo es el mapa de Peters. Ambas son proyecciones posibles de las muchas que hay. Como afirmó Arthur Robinson, una proyección no es ni buena ni mala; solo pueden resultar acertadas o desacertadas las elecciones que podemos hacer en relación con un determinado tema o propósito (Rabella 2013).
4.4 Winkel-Tripel
La proyección de Winkel Tripel, presentada por Oswald Winkel en Alemania en 1921, está entre una proyección conforme y una proyección equivalente.
La proyección se obtiene haciendo una media de las coordenadas de las proyecciones equidistante cilíndrica y de Aitoff. Winkel añade el nombre Tripel, que normalmente significa ‘triple’, porque la proyección de Aitoff tiene un punto de vista ecuatorial de un hemisferio de la proyección equidistante acimutal, en la cual las coordenadas horizontales se han duplicado y a los meridianos se los ha dado dos veces sus longitudes originales.
El meridiano central es recto. Los otros meridianos son curvos, igualmente espaciados a lo largo del ecuador y cóncavos hacia el meridiano central. El ecuador y los polos son rectos. Los otros paralelos son curvos, igualmente espaciados a lo largo del meridiano central y cóncavos hacia el polo más próximo. Los polos son líneas rectas alrededor de 0,4 veces el ecuador en función de la latitud de los paralelos estándares. La escala es verdadera a lo largo del meridiano central y constante a lo largo del ecuador.
Como se observa en la figura 4.4, la distorsión es moderada, excepto cerca de los meridianos exteriores de las regiones polares. La Winkel Tripel se utiliza para los mapas que incluyan todo el mundo y es la aceptada actualmente por la National Geographic Society (NGS).
4.5 Cónica conforme de Lambert
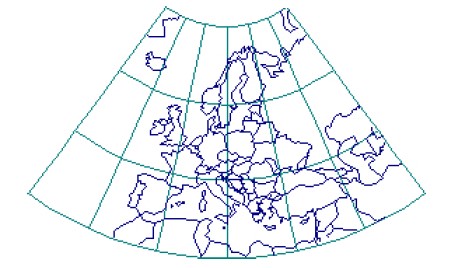
La proyección cónica conforme de Lambert (CCL), presentada por Johann Heinrich Lambert en 1772 (figura 4.5), muestra los meridianos como líneas rectas equidistantes que convergen en uno de los polos. Los ángulos entre los meridianos en la proyección son más pequeños que los ángulos correspondientes al globo. Los paralelos son arcos circulares concéntricos espaciados desigualmente y centrados en el polo, de tal manera que el espaciamiento entre los paralelos aumenta según se alejan del polo. El polo más próximo al paralelo estándar es un punto, y el otro polo no se puede mostrar. La escala es verdadera a lo largo del paralelo estándar o a lo largo de dos paralelos estándares, y es constante a lo largo de cualquier paralelo determinado. La proyección cónica conforme de Lambert se utiliza ampliamente para la cartografía a gran escala de las regiones con un eje este-oeste pronunciado y en regiones de latitud mediana. Es habitual en muchos países para mapas a escala 1:500.000, y para las cartas aeronáuticas a una escala similar.
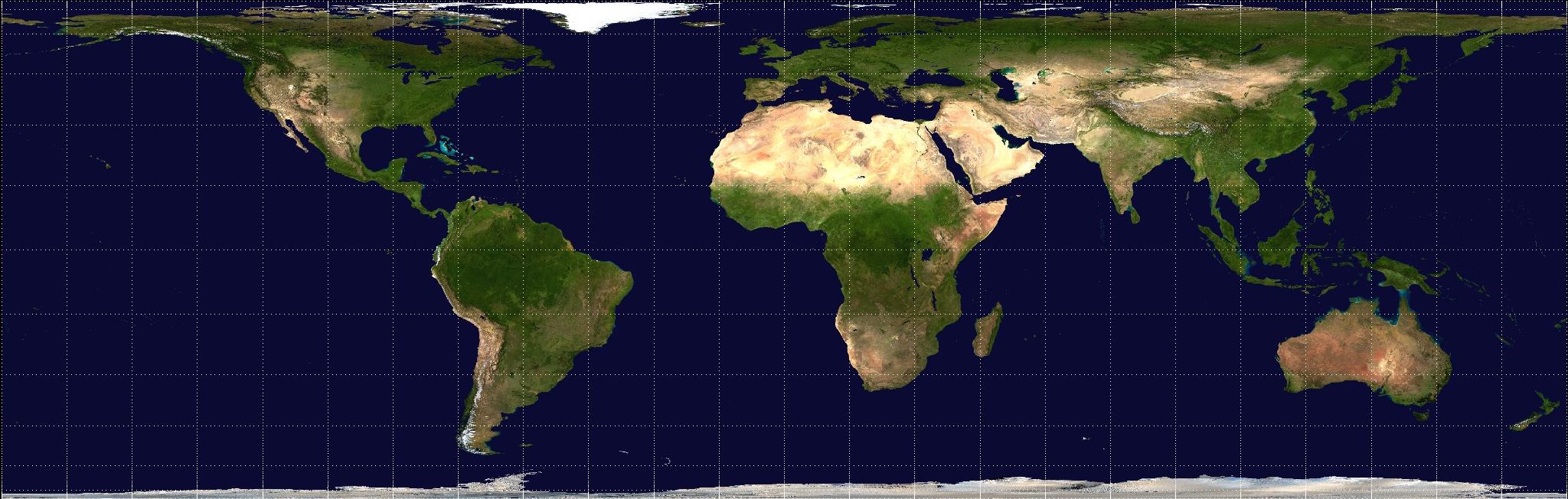
4.5.1 Proyección cilíndrica equivalente de Lambert
La proyección cilíndrica equivalente de Lambert (de áreas equivalentes) fue presentada por primera vez por Johann Heinrich Lambert en 1772 y se convirtió en la base para otras muchas proyecciones equivalentes similares, incluida la de Gall, la de Behrmann y las proyecciones de Trystan Edwards (figura 4.6). La proyección original de Lambert utiliza una sola línea de escala constante a lo largo de la línea del ecuador. Se elaboran proyecciones equivalentes similares utilizando dos paralelos, como las líneas de escala constante. En la proyección cilíndrica equivalente de Lambert, los meridianos son líneas rectas paralelas y equidistantes, y el ecuador es π veces más largo que los meridianos. Las líneas de latitud son líneas paralelas espaciadas desigualmente, más alejadas cuanto más cerca del ecuador, y perpendiculares a los meridianos. Cambiar el espaciamiento de los paralelos es el método utilizado para preservar áreas iguales. Sin embargo, las importantes distorsiones de distancias y ángulos dan lugar a una distorsión más grande en latitudes altas cerca de los polos. Esta proyección a menudo no se utiliza directamente para la elaboración de mapas, pero representa un estándar para describir los principios de las proyecciones cartográficas en libros de texto, y también ha servido como prototipo para otras proyecciones.
Quien quiera profundizar en aspectos más técnicos de la cartografía, puede consultar el libro siguiente: Santamaría Peña, J. (2011). La Cartografía y las proyecciones cartográficas. Ingenierías, 15. Universidad de La Rioja.
4.6 Investigación sobre nuevas proyecciones de mapas
En 2007 B. Jenny, T. Patterson y L. Hurni produjeron, inspirados por el método de Robinson, el programa interactivo Flex Proyector, que permite al usuario crear nuevas proyecciones de mapas del mundo con facilidad. Es compatible con el punto de vista normal de las proyecciones cilíndricas. El programa es gratuito, de código abierto, y funciona en Linux, Mac OS X y Windows. Al ejecutar el programa, aparece en la pantalla un mapamundi en la proyección de Robinson (ved la figura 4.7).
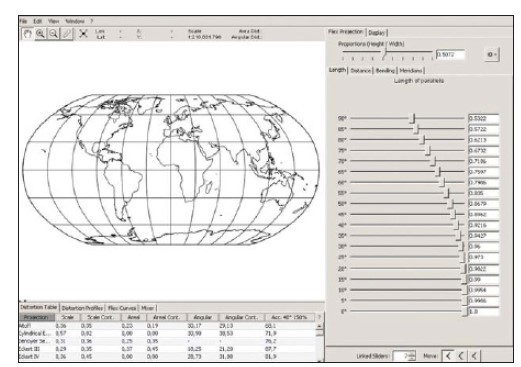
El objetivo de esta investigación es desarrollar una alternativa a la proyección de Web Mercator para los mapas a escala pequeña de la web, donde los mapas utilizan automáticamente una proyección óptima en función de la escala del mapa, su relación altura-anchura y la latitud central del área mostrada.
4.7 Conclusiones
La razón por la cual tenemos tantas proyecciones cartográficas es porque ninguna funciona perfectamente para todo. La elección de una proyección cartográfica apropiada para una determinada aplicación depende de varios factores, incluidos el propósito del mapa, el tipo de datos que se quiere representar, la región del mundo donde se proyecta y la escala final del mapa. En los sistemas de información geográfica (SIG) con bases de datos a gran escala (para áreas pequeñas), se utilizan proyecciones conformes para preservar los ángulos. Para estas aplicaciones, la distorsión de áreas es tan pequeña sobre la extensión geográfica que es insignificante y no es necesario el uso de una proyección que conserve áreas. Habitualmente, los archivos de datos a gran escala se utilizan en aplicaciones SIG de extensión geográfica limitada (por ejemplo, un condado o un estado). Las dos proyecciones más utilizadas para estas escalas son la cónica conforme de Lambert y la transversal de Mercator, que son la base de la UTM y de la mayor parte del sistema de coordenadas del USA State Plane. Para mapamundis de consulta general, se recomienda no utilizar cualquier proyección cilíndrica, sino una de pseudocilíndrica (por ejemplo, la de Robinson, o una proyección de compromiso como la de Winkel-Tripel).
En resumen, las proyecciones cartográficas y las transformaciones de coordenadas son la base de la consecución de un marco común de referencia para la información geográfica. El requisito de tener un elipsoide, un datum, una proyección cartográfica y finalmente un sistema de coordenadas planas, todos comunes, hacen posible el uso de la geometría plana para todo tipo de superposiciones y análisis espaciales. La proyección de los datos geográficos de la Tierra elipsoidal sobre un sistema de coordenadas planas siempre se traduce en una distorsión de las superficies, formas, distancias y otras propiedades. Con la elección apropiada de una proyección, el usuario puede conservar las características que quiere a costa de otras y mostrar la proyección geográfica que quiere con más precisión.