11 Variables
11.1 Introducció
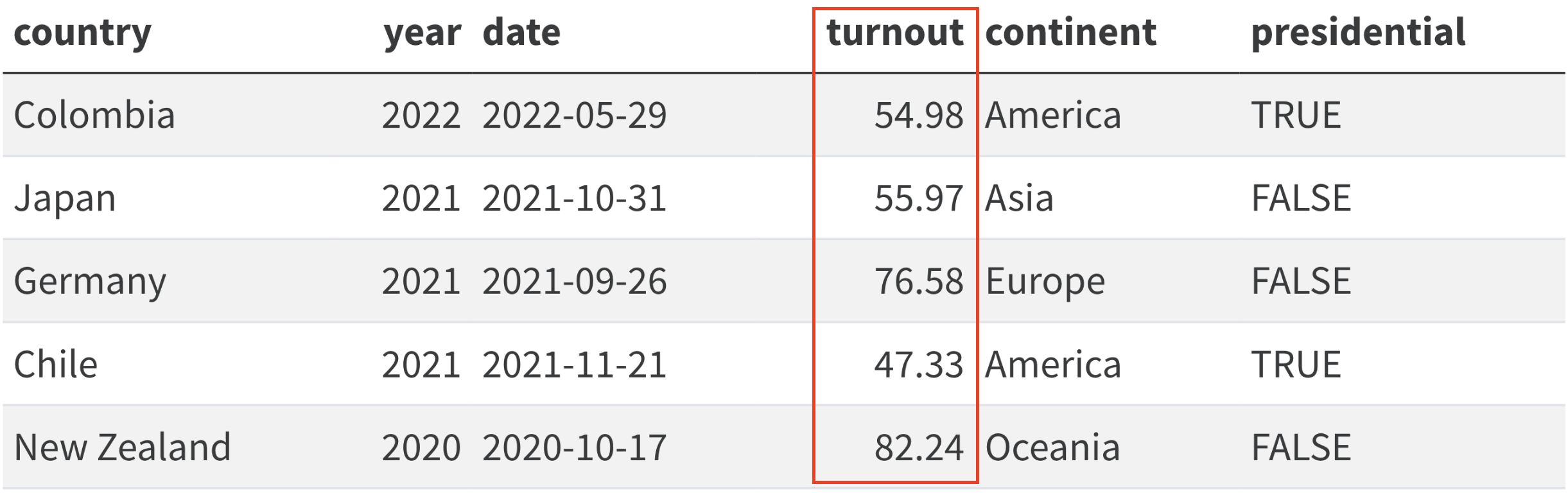
Una variable és una característica del fenomen que volem estudiar que varia entre observacions i que, per tant, pren diversos valors. Si una determinada característica pren el mateix valor a totes les observacions del marc de dades, llavors no és una variable, simplement, perquè no varia. Tornem a explorar el marc de dades d’eleccions, però aquesta vegada veiem assenyalada en vermell una de les seves variables a la figura 11.1. La columna turnout és una característica del fenomen que estem estudiant, que són les eleccions. I és per tant una variable perquè adopta diferents valors: 54.98, 55.97, etc. El nom del país també és una característica de cada unitat, ja que ens indica el nom del país on s’han produït les eleccions. Totes elles, si ens hi fixem, són variables. En canvi, no seria una variable el planeta on s’han produït les eleccions, perquè totes s’han produït a la Terra. La gravetat també seria la mateixa i a cada observació també hi ha la mateixa presència d’oxigen, per la qual cosa aquestes dues característiques, si estiguessin en aquest conjunt de dades, no les podríem considerar variables.
Com podem veure, les variables acostumen a estar formades per nombres (com els valors de turnout o de year), o bé per categories (com els valors de country o de continent). Però al marge d’aquesta primera distinció, l’important és distingir-les per les operacions que permeten fer amb els seus valors. A la taula 11.1 observem els quatre tipus principals de variables. Amb les variables nominals, només podem saber si els seus valors són iguals o diferents. En canvi, amb les variables ordinals també podem ordenar els seus valors. A diferència de les ordinals, les variables d’interval tenen valors amb significat, per la qual cosa en algunes ocasions podrem fer operacions com sumes i restes. I finalment, amb les variables de ràtio podrem fer tot tipus d’operacions, com sumar, restar, multiplicar o dividir.
| Tipus | Característiques | Vector | Operacions |
|---|---|---|---|
| Categòrica nominal | Categories no ordenables | Caràcter o factor |
==, !=
|
| Categòrica ordinal | Categories ordenables | Factor |
==, !=, <=, <, >, >=
|
| Numèrica d’interval | Nombres, zero sense significat | Numèric o enter |
==, !=, <=, <, >, >=, +, -
|
| Numèrica de ràtio | Nombres, zero amb significat | Numèric |
==, !=, <=, <, >, >=, +, -, *, / … |
Fins ara hem estudiat la columna, la variable i el vector com tres conceptes que semblen idèntics. Però són el mateix? La resposta és que no, encara que és fàcil confondre’ls l’un per l’altre perquè sovint serveixen per al mateix propòsit. Per distingir-los, direm que:
- La columna es refereix a la distribució vertical dels valors en una taula.
- La variable és un constructe abstracte, una propietat del fenomen que estem estudiant que varia entre observacions.
- El vector és una eina d’R que ens permet emmagatzemar dades en forma de concatenat.
Malgrat aquestes diferències, és ben cert que moltes vegades la columna, la variable i el vector se solapen. Per analitzar fenòmens, a R acostumem a guardar les variables en forma de vectors. I cada vector forma una columna d’un marc de dades. Més endavant veurem, però, que no sempre hi ha coincidència (vegeu per exemple el marc de dades tidyr::world_bank_pop, en què les variables són valors de la columna indicator i els anys són noms de variables en lloc de valors).
11.2 Variables nominals
Les variables categòriques nominals (també en podem dir simplement variables nominals) agrupen els seus valors en categories diferents assumint que no segueixen cap ordre concret. L’únic que podem fer és classificar-les. Podem, per exemple, classificar pel seu nom els estats que hi ha al món, els colors, les religions, la nacionalitat d’una persona, el lloc de naixement o el sexe. Però no podem ni ordenar ni quantificar aquestes característiques numèricament: no té sentit dir que el nom «groc» és superior a «blau» o multiplicar «Brasil» per «Hondures». L’únic que podem fer és dir si un valor de la variable és igual o diferent d’un altre.
A R, emmagatzemarem les variables nominals com a vectors de caràcter o com a factors. En essència, no hi ha cap diferència en guardar una variable nominal en un vector de caràcter o en un factor.
11.2.1 Operacions amb variables nominals
Per fer algunes operacions amb variables nominals, hem creat el marc de dades strings a partir d’una adaptació de les dades del paquet countrycode (Arel-Bundock, 2022). En l’argot d’R, la paraula string s’utilitza per denominar els vectors de caràcter:
strings <- tribble(~iso3c, ~country, ~currency, ~continent, ~region,
"CMR", "Cameroon", "CFA Franc BEAC", "Africa", "Sub-Saharan Africa",
"COL", "Colombia", "Colombian Peso", "Americas", "Latin America & Caribbean",
"CUB", "Cuba", "Cuban Peso", "Americas", "Latin America & Caribbean",
"FRA", "France", "Euro", "Europe", "Europe & Central Asia",
"LSO", "Lesotho", "Loti", "Africa", "Sub-Saharan Africa",
"QAT", "Qatar", "Qatari Rial", "Asia", "Middle East & North Africa",
"TWN", "Taiwan", "New Taiwan Dollar", "Asia", "East Asia & Pacific",
"TTO", "Trinidad & Tobago", "Trinidad & Tobago Dollar", "Americas", "Latin America & Caribbean")
strings
## # A tibble: 8 × 5
## iso3c country currency continent region
## <chr> <chr> <chr> <chr> <chr>
## 1 CMR Cameroon CFA Franc BEAC Africa Sub-Saharan Africa
## 2 COL Colombia Colombian Peso Americas Latin America & Ca…
## 3 CUB Cuba Cuban Peso Americas Latin America & Ca…
## 4 FRA France Euro Europe Europe & Central A…
## 5 LSO Lesotho Loti Africa Sub-Saharan Africa
## 6 QAT Qatar Qatari Rial Asia Middle East & Nort…
## 7 TWN Taiwan New Taiwan Dollar Asia East Asia & Pacific
## 8 TTO Trinidad & Tobago Trinidad & Tobago Dollar Americas Latin America & Ca…Amb les operacions que veiem al requadre de la dreta, podem respondre preguntes com les que fem a continuació:
En tenir poques propietats matemàtiques, amb les variables nominals només podem fer operacions de:
- Igualtat (
==,%in%) - No igualtat (
!=)
%in%
Amb operacions amb més d’un valor categòric, utilitzarem %in%. Per exemple, si del vector var volem que ens retorni v1, v2 i v3, utilitzarem el codi següent:
var %in% c("v1","v2","v3") Quina observació és Cameroon? Del marc de dades strings, seleccionem les observacions en què la variable country sigui igual a "Cameroon".
strings[strings$country == "Cameroon",]
## # A tibble: 1 × 5
## iso3c country currency continent region
## <chr> <chr> <chr> <chr> <chr>
## 1 CMR Cameroon CFA Franc BEAC Africa Sub-Saharan AfricaQuins països estan a l’Àfrica o a Europa? Del marc de dades strings, seleccionem les observacions en què la variable continent sigui igual a "Africa" o "Europe".
strings[strings$continent %in% c("Africa", "Europe"),]
## # A tibble: 3 × 5
## iso3c country currency continent region
## <chr> <chr> <chr> <chr> <chr>
## 1 CMR Cameroon CFA Franc BEAC Africa Sub-Saharan Africa
## 2 FRA France Euro Europe Europe & Central Asia
## 3 LSO Lesotho Loti Africa Sub-Saharan AfricaQuins països no estan a la regió d’Amèrica Llatina i el Carib? Del marc de dades strings, seleccionem les observacions en què la variable region sigui no igual a "Latin America & Caribbean".
strings[strings$region != "Latin America & Caribbean",]
## # A tibble: 5 × 5
## iso3c country currency continent region
## <chr> <chr> <chr> <chr> <chr>
## 1 CMR Cameroon CFA Franc BEAC Africa Sub-Saharan Africa
## 2 FRA France Euro Europe Europe & Central Asia
## 3 LSO Lesotho Loti Africa Sub-Saharan Africa
## 4 QAT Qatar Qatari Rial Asia Middle East & North Africa
## 5 TWN Taiwan New Taiwan Dollar Asia East Asia & PacificMés endavant, veurem com amb altres variables podrem fer operacions més complexes. Com que les categories de les variables nominals no són ordenables, no permeten saber si una categoria és més gran que l’altra o sumar i restar categories. No obstant això, hem de saber que els vectors de caràcter i els factors tenen associada una ordenabilitat alfabètica1.
1 Els vectors de caràcter, i també els factors, estan ordenats alfabèticament, on «A» és el valor més petit i «Z» el valor més gran. Aquesta ordenació ens pot convenir puntualment, però no haurem de concebre les variables nominals com a ordenables.
11.2.2 Altres exemples de variables nominals
A la base de dades següent veiem un fragment de la Global Terrorism Database (START, 2022), que té recomptats més de 200.000 atacs terroristes des de 1970 fins a l’actualitat, incloent-hi bombardejos, assassinats i segrestos. Com podem veure a la taula 11.2, les variables country_txt, provstate, city, attacktype1_txt, targtype1_txt i weapdetail són nominals2.
2 Podríem pressuposar certa ordinalitat a attacktype1_txt i weapdetail.
| iyear | country_txt | provstate | city | latitude | longitude | attacktype1 | attacktype1_txt | targtype1 | targtype1_txt | weapdetail |
|---|---|---|---|---|---|---|---|---|---|---|
| 1970 | Dominican Republic | National | Santo Domingo | 18.45679 | -69.95116 | 1 | Assassination | 14 | Private Citizens & Property | NA |
| 1970 | Mexico | Federal | Mexico city | 19.37189 | -99.08662 | 6 | Hostage Taking (Kidnapping) | 7 | Government (Diplomatic) | NA |
| 1970 | Philippines | Tarlac | Unknown | 15.47860 | 120.59974 | 1 | Assassination | 10 | Journalists & Media | NA |
| 1970 | Greece | Attica | Athens | 37.99749 | 23.76273 | 3 | Bombing/Explosion | 7 | Government (Diplomatic) | Explosive |
| 1970 | Japan | Fukouka | Fukouka | 33.58041 | 130.39636 | 7 | Facility/Infrastructure Attack | 7 | Government (Diplomatic) | Incendiary |
| 1970 | United States | Illinois | Cairo | 37.00511 | -89.17627 | 2 | Armed Assault | 3 | Police | Several gunshots were fired. |
| 1970 | Uruguay | Montevideo | Montevideo | -34.89115 | -56.18721 | 1 | Assassination | 3 | Police | Automatic firearm |
| 1970 | United States | California | Oakland | 37.79193 | -122.22591 | 3 | Bombing/Explosion | 21 | Utilities | NA |
També hem vist anteriorment en bases de dades d’aquest capítol exemples de variables nominals:
- El nom del país (
ctryname) a la taula 10.5. - El nom del líder polític (
leader) a la taula 10.8. - El nom del grup ètnic (
group) a la taula 10.6.
Altres variables nominals poden ser el municipi (Barcelona, Sant Cugat, Granollers…), la religió (musulmana, catòlica, sintoista…), la llengua (rus, català, suec…), la ideologia (conservadora, progressista, liberal…), l’organització internacional (Unió Europea, Mercosur, ASEAN…) o el tipus de mercaderia (transport, maquinària, tèxtil…).
11.2.3 Variables binàries
Les variables binàries (també dites dicotòmiques o dummy) són conceptualment un subtipus de variable categòrica nominal en què la característica de l’objecte que estem estudiant només pot adoptar dos valors: absència o presència (Goertz, 2020, pàg. 137–138). Operativament, però, podem tractar aquestes variables com a vector de caràcter, com a factor, com a vector numèric i fins i tot com a vector lògic. No hi ha cap norma clara de com guardar-les inicialment. El més normal és que més endavant les transformem d’un tipus de vector a un altre en funció del nostre propòsit3.
3 Per exemple, si volem visualitzar dades, les acabarem transformant en vectors de caràcter o factors, mentre que si volem realitzar una anàlisi bivariant les acabarem transformant a vectors numèrics. Passar-la a vector lògic és factible, però poc habitual.
Quan importem dades a R, el més freqüent serà trobar-nos les variables binàries codificades en un vector numèric amb 1 i 0. El valor 1 indicarà la presència del concepte i el 0 l’absència. En la següent taula 11.3, observem un fragment de la Formal Alliances dataset (Gibler, 2009; Singer & Small, 1966), formada principalment per variables binàries. Cada unitat d’observació és l’aliança entre dos països. Entre les seves característiques, s’hi troba l’any de creació (dyad_st_year), l’any de finalització (dyad_end_year), si és una aliança de defensa (defense), de neutralitat (neutrality), un pacte de no-agressió (nonaggression) o una entente (entente).
| version4id | state_name1 | state_name2 | dyad_st_year | dyad_end_year | defense | neutrality | nonaggression | entente |
|---|---|---|---|---|---|---|---|---|
| 1 | United Kingdom | Portugal | 1816 | NA | 1 | 0 | 1 | 0 |
| 2 | United Kingdom | Sweden | 1816 | 1911 | 0 | 0 | 0 | 1 |
| 3 | Hanover | Bavaria | 1838 | 1848 | 1 | 0 | 1 | 1 |
| 3 | Hanover | Bavaria | 1850 | 1866 | 1 | 0 | 1 | 1 |
| 3 | Hanover | Germany | 1850 | 1866 | 1 | 0 | 1 | 1 |
| 3 | Hanover | Germany | 1838 | 1848 | 1 | 0 | 1 | 1 |
| 3 | Hanover | Baden | 1838 | 1848 | 1 | 0 | 1 | 1 |
| 3 | Hanover | Baden | 1850 | 1866 | 1 | 0 | 1 | 1 |
Quan ens trobem alguna variable binària en un marc de dades, el més recomanable és deixar-la com està. Normalment, això significarà deixar-la com a vector numèric i, en tot cas, ja recodificarem la variable més endavant si ho necessitem. En el cas que volguéssim passar la variable a categòrica, recomanem emmagatzemar-la en forma de factor. Si suposem que el marc de dades té com a nom ally, utilitzaríem el procediment següent per convertir la variable defense a factor4.
4 El mateix podríem fer amb neutrality, nonaggression i entente.
En aquest capítol hem vist diversos exemples de variables binàries. Per exemple:
- Si el líder polític va ser o no elegit (
elected) a la taula 10.8. - Si un cop d’estat va ser exitós o no (
successful) a la taula 10.7. - Si el grup ètnic té autonomia regional o no (
reg_aut) a la taula 10.6.
El que és important és que el nom del vector numèric permeti identificar clarament quin sentit pren la variable en cas de presència. El vector male no tindria sentit posar-lo com a sex si està codificat amb 1 i 0, perquè no sabríem quin sexe és 1 i quin és 0. En canvi, si la recodifiquéssim com a factor, sí que tindria més sentit posar sex i que tingués com a possibles valors «Male» i «Female» o bé «Other».
11.2.4 El paquet stringr
Per manipular els vectors de caràcter, la millor eina que podem utilitzar és el paquet stringr (Wickham, 2023b). En aquest apartat no explicarem totes les funcions del paquet. El més adequat és consultar el seu Cheatsheet corresponent a la pàgina d’RStudio. Però a continuació veurem algunes funcions amb el mateix marc de dades strings que hem creat anteriorment:
Amb str_remove() podem eliminar una sèrie de caràcters dels valors d’una variable. A continuació, eliminem "Latin " (pareu atenció a l’espai) de la variable region.
str_remove(strings$region, "Latin ")
## [1] "Sub-Saharan Africa" "America & Caribbean"
## [3] "America & Caribbean" "Europe & Central Asia"
## [5] "Sub-Saharan Africa" "Middle East & North Africa"
## [7] "East Asia & Pacific" "America & Caribbean"Amb str_replace() podem substituir uns caràcters per uns altres. A continuació, substituïm «&» de la variable country per «and».
str_replace(strings$country, "&", "and")
## [1] "Cameroon" "Colombia" "Cuba"
## [4] "France" "Lesotho" "Qatar"
## [7] "Taiwan" "Trinidad and Tobago"Amb str_to_upper() posem tots els caràcters en majúscules. A continuació, posem el nom de la moneda de la variable currency en majúscules.
str_to_upper(strings$currency)
## [1] "CFA FRANC BEAC" "COLOMBIAN PESO"
## [3] "CUBAN PESO" "EURO"
## [5] "LOTI" "QATARI RIAL"
## [7] "NEW TAIWAN DOLLAR" "TRINIDAD & TOBAGO DOLLAR"D’una manera molt semblant, str_to_sentence() posa la primera lletra de la frase en majúscula, str_to_lower() totes les lletres en minúscules, str_to_title() la primera lletra de cada paraula en majúscules.
Amb str_sub() traiem l’últim caràcter de la variable iso3c, de manera que ens queda un codi de país de dos caràcters.
str_sub(strings$iso3c, end = 2)
## [1] "CM" "CO" "CU" "FR" "LS" "QA" "TW" "TT"11.3 Variables ordinals
Les variables categòriques ordinals (o, simplement, variables ordinals) agrupen les observacions en categories diferents que segueixen un ordre lògic concret. Per exemple, podem ordenar les persones en funció de si són «infants», «joves» o «adults» o bé el seu nivell educatiu en «sense estudis», «estudis primaris», «estudis secundaris» o «estudis superiors». Així, podem saber si una categoria és superior o inferior a l’altra. El que no podem saber amb aquesta variable és la distància que hi ha entre categories. No sabem, per exemple, si hi ha la mateixa distància entre «sense estudis» i «estudis primaris» que entre «estudis primaris» i «estudis secundaris», simplement pel fet que no hi ha cap interval numèric associat a cada variable. L’únic que podem fer és comparar les categories entre elles en termes de ser més, menys, igual que o diferent a una altra.
A R, emmagatzemarem les variables ordinals com a factors ordenables.
11.3.1 Operacions amb variables ordinals
Per fer algunes operacions amb variables ordinals hem creat el marc de dades ords, que conté una classificació d’agències donants d’ajuda al desenvolupament i la seva puntuació ordinal en el rànquing Aid Transparency Index (ATI) de 2022 que publica per l’ONG Publish What You Fund. Aquesta classificació ordinal estableix fins a quin punt l’agència donant publica de forma transparent què es gasta, qui ho gasta i a on es gasta. El marc de dades també inclou a quin tipus de règim pertany l’agència donant segons la classificació ordinal de democràcia de l’Economist Intelligence Unit de 2022.
ords <- tibble(donor = c("US-MCC", "Canada-GAC", "Germany-BMZ-GIZ", "Korea-KOICA", "Australia-DFAT", "Spain-AECID",
"Saudi Arabia-KSRelief", "Norway-MFA", "China-MOFCOM", "Turkey-TIKA"),
ati = factor(c("Very Good", "Good", "Good", "Good", "Good", "Fair",
"Poor", "Poor", "Very Poor", "Very Poor"),
ordered = TRUE,
levels = c("Very Poor", "Poor", "Fair", "Good", "Very Good")),
regime_type = factor(c("Flawed Democracy", "Full Democracy", "Full Democracy", "Full Democracy", "Full Democracy",
"Flawed Democracy", "Authoritarian", "Full Democracy", "Authoritarian", "Hybrid Regime"),
ordered = TRUE,
levels = c("Authoritarian", "Hybrid Regime", "Flawed Democracy", "Full Democracy")))
ords
## # A tibble: 10 × 3
## donor ati regime_type
## <chr> <ord> <ord>
## 1 US-MCC Very Good Flawed Democracy
## 2 Canada-GAC Good Full Democracy
## 3 Germany-BMZ-GIZ Good Full Democracy
## 4 Korea-KOICA Good Full Democracy
## 5 Australia-DFAT Good Full Democracy
## 6 Spain-AECID Fair Flawed Democracy
## 7 Saudi Arabia-KSRelief Poor Authoritarian
## 8 Norway-MFA Poor Full Democracy
## 9 China-MOFCOM Very Poor Authoritarian
## 10 Turkey-TIKA Very Poor Hybrid RegimeAmb les operacions que veiem al requadre de la dreta, podem respondre preguntes com les que fem a continuació:
Amb les variables ordinals podem fer operacions de:
- Igualtat (
==,%in%) - No igualtat (
!=) - Més gran que (
>) - Més gran o igual que (
>=) - Més petit que (
<) - Més petit o igual que (
<=)
Quines agències pertanyen a democràcies dèbils? Del marc de dades ords, seleccionem les observacions en què la variable regime_type sigui igual a "Flawed Democracy".
ords[ords$regime_type == "Flawed Democracy",]
## # A tibble: 2 × 3
## donor ati regime_type
## <chr> <ord> <ord>
## 1 US-MCC Very Good Flawed Democracy
## 2 Spain-AECID Fair Flawed DemocracyQuines agències tenen un ATI com a mínim bo? Del marc de dades ords, seleccionem les observacions en què la variable ati sigui major o igual que "Good".
ords[ords$ati >= "Good",]
## # A tibble: 5 × 3
## donor ati regime_type
## <chr> <ord> <ord>
## 1 US-MCC Very Good Flawed Democracy
## 2 Canada-GAC Good Full Democracy
## 3 Germany-BMZ-GIZ Good Full Democracy
## 4 Korea-KOICA Good Full Democracy
## 5 Australia-DFAT Good Full DemocracyQuines agències tenen un ATI inferior a correcte? Del marc de dades ords, seleccionem les observacions en què la variable ati sigui menor que "Fair".
ords[ords$ati < "Fair",]
## # A tibble: 4 × 3
## donor ati regime_type
## <chr> <ord> <ord>
## 1 Saudi Arabia-KSRelief Poor Authoritarian
## 2 Norway-MFA Poor Full Democracy
## 3 China-MOFCOM Very Poor Authoritarian
## 4 Turkey-TIKA Very Poor Hybrid RegimeA part de les operacions d’igualtat, doncs, les variables ordinals permeten saber si una categoria és més gran o més petita que l’altra. Però com que no coneixem la distància entre categories, per exemple entre «Fair» i «Poor», no podem fer operacions més complexes com sumar i restar. Aquestes operacions les podrem fer amb les variables numèriques.
11.3.2 Importar dades ordinals
Quan importem bases de dades a R, rarament ens trobarem les variables ordinals codificades com a factor ordinal. Normalment ens trobarem una de les situacions següents:
| code | income_group |
|---|---|
| AFG | Low income |
| ALB | Upper middle income |
| DZA | Upper middle income |
| ASM | Upper middle income |
| AND | High income |
| AGO | Lower middle income |
| ATG | High income |
| ARG | Upper middle income |
Les variables ordinals estan codificades com a vector de caràcter (1). Aquest és el cas, per exemple, de la variable
income_group, una classificació produïda pel Banc Mundial que ordena grups de països segons nivells de renda per càpita. Observem un fragment d’aquestes dades a la taula 11.4 del lateral.Les variables ordinals ens arriben codificades com a vector numèric (2). Aquest és el cas de moltes dades d’enquesta, en què respostes que porten associades categories com «Molt», «Bastant», «Poc» o «Gens» acostumen a estar codificades numèricament (taula 11.5).
En tots dos casos, les variables hauran de ser recodificades a factor ordinal amb un procediment molt semblant. Per ara, hem de saber que per fer la conversió utilitzarem la funció factor() i a dins hi introduirem tres arguments: el vector, la indicació que és ordinal en el vector ordrered i, en un tercer argument, els nivells (levels) o bé les etiquetes (labels) del factor.
| CCOW | YEAR | Q1 | Q2 | Q3 | Q4 |
|---|---|---|---|---|---|
| AND | 2018 | 1 | 1 | 1 | 3 |
| AND | 2018 | 1 | 1 | 1 | 4 |
| AND | 2018 | 1 | 2 | 2 | 2 |
| AND | 2018 | 1 | 1 | 1 | 4 |
| AND | 2018 | 1 | 1 | 1 | 3 |
| AND | 2018 | 1 | 3 | 1 | 4 |
factor(vector,
ordered = TRUE,
levels = c("Baix", "Mig", "Alt"))A l’apartat Recodificacions de variables tractarem aquests dos casos en detall i veurem també la diferència entre levels i labels.
Un resum dels operadors relacionals que hem vist ara el trobem en aquest vídeo:
11.3.3 El paquet forcats
Per manipular els factors, la millor eina que podem utilitzar és el paquet forcats (Wickham, 2023a). En aquest apartat només veurem algunes de les seves funcions, però per explorar-lo més a fons podeu consultar el seu Cheatsheet corresponent a la pàgina d’RStudio. A continuació aplicarem algunes funcions al marc de dades ords que hem creat anteriorment. La majoria d’aquestes funcions van relacionades amb reordenar factors i són molt útils per a la visualització de gràfics.
Amb fct_relevel() canviem ràpidament l’ordre dels nivells. En el primer argument indiquem el factor i en la resta d’arguments indiquem, en ordre ascendent, els nivells.
fct_relevel(ords$regime_type, "Hybrid Regime", "Full Democracy", "Flawed Democracy", "Authoritarian")
## [1] Flawed Democracy Full Democracy Full Democracy Full Democracy
## [5] Full Democracy Flawed Democracy Authoritarian Full Democracy
## [9] Authoritarian Hybrid Regime
## 4 Levels: Hybrid Regime < Full Democracy < ... < AuthoritarianAmb fct_rev() capgirem l’ordre dels nivells.
fct_rev(ords$ati)
## [1] Very Good Good Good Good Good Fair Poor
## [8] Poor Very Poor Very Poor
## Levels: Very Good < Good < Fair < Poor < Very PoorAmb fct_other() creem un nivell format per diverses categories. En el primer argument indiquem el factor i en el segon indiquem les categories que volem conservar.
fct_other(ords$ati, keep = c("Good", "Very Good"))
## [1] Very Good Good Good Good Good Other Other
## [8] Other Other Other
## Levels: Good < Very Good < OtherAmb fct_infreq() ordenem els nivells en funció del seu nombre de freqüències a la base de dades (és a dir, en funció de les vegades que hi apareixen). Aquesta funció és molt útil quan la combinem amb funcions que reprodueixen gràfics.
plot(fct_infreq(ords$ati))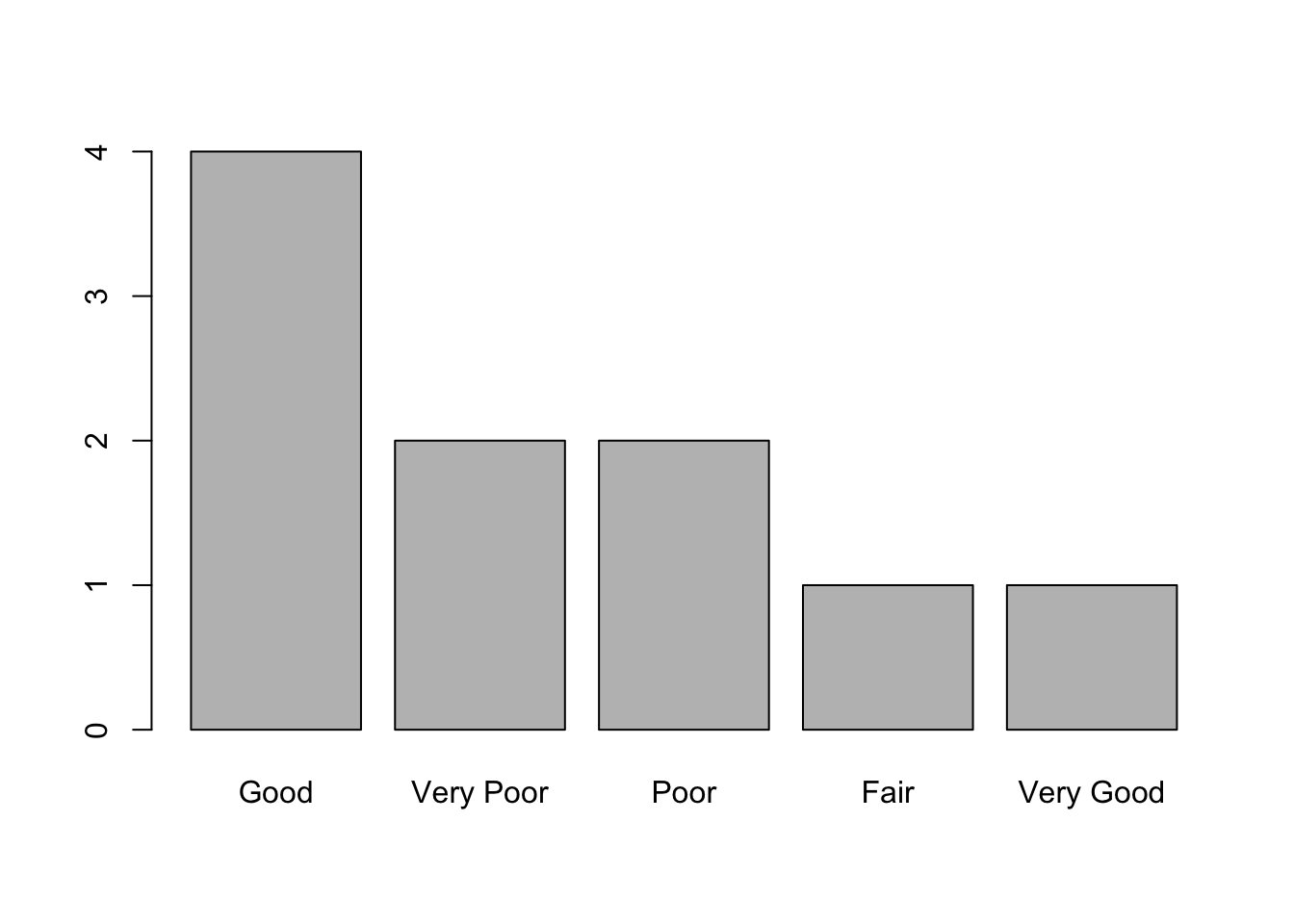
Si combinem fct_infreq() i fct_rev(), obtindrem els nivells en l’ordre contrari.
plot(fct_rev(fct_infreq(ords$ati)))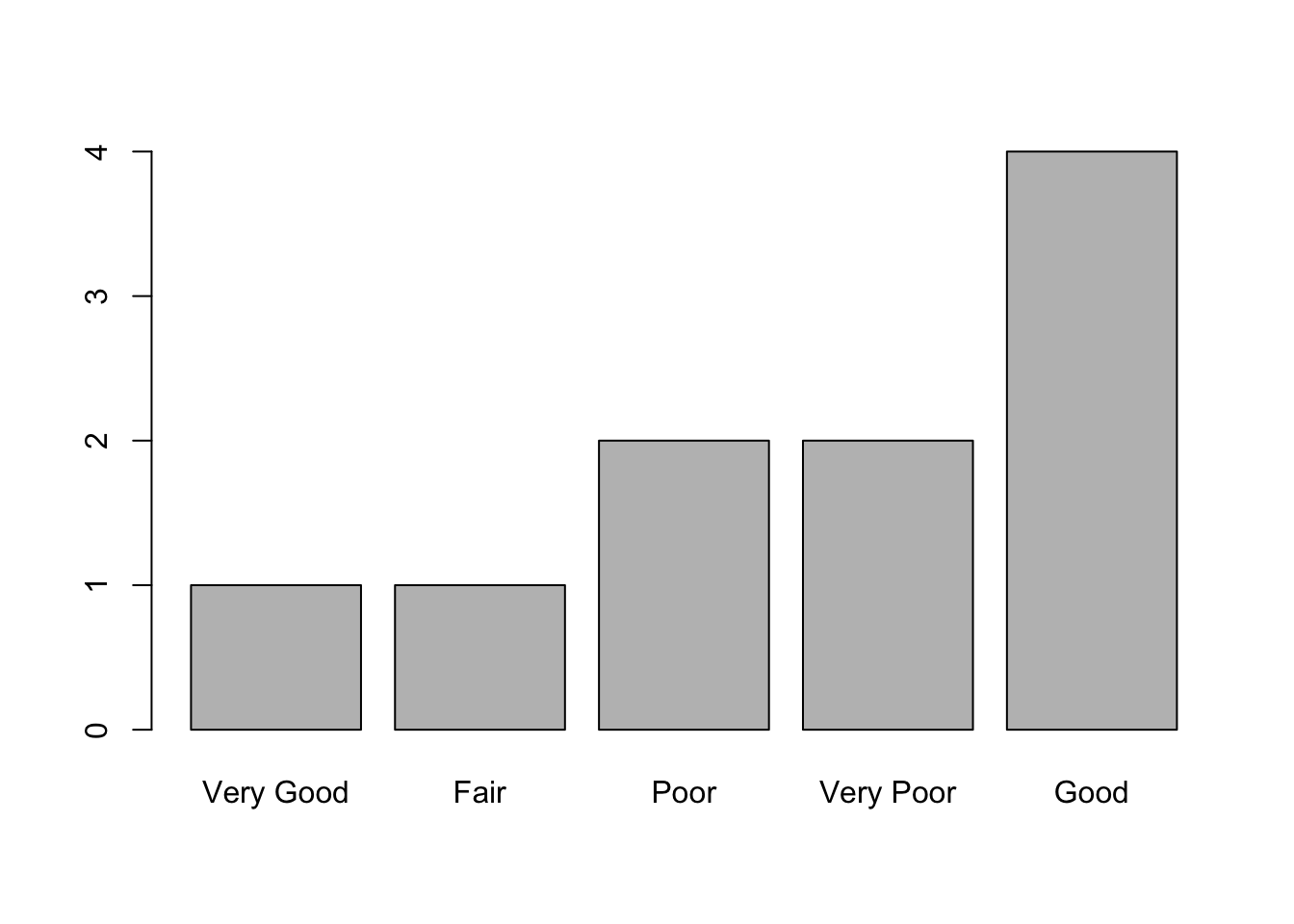
Totes les funcions de forcats són útils per factors, tant per representar variables nominals com per representar variables ordinals.
11.4 Variables d’interval
A diferència de les variables categòriques, les variables numèriques agrupen les observacions en nombres. Les variables numèriques d’interval (o simplement variables d’interval) tenen com a principal propietat que la distància entre els seus valors té significat, però que el valor zero no indica l’absència del valor en concret. Així, amb les variables d’interval podem fer les mateixes operacions que amb les variables ordinals (saber si un valor és més gran o més petit que un altre) i, a més, també podem saber com de gran o com de petit és aquest valor perquè la distància numèrica és coneguda.
Un exemple és la variable any, quan ens referim als anys de calendari5. Posem pel cas que tenim tres valors d’interval: 1919, 1945 i 1989. Podem saber si un any és més petit o més gran que l’altre, però també podem saber quina distància hi ha entre aquests valors. Per exemple, sabem que hi ha una diferència de 26 anys entre 1919 i 1945 i una diferència de 70 anys entre 1919 i 1989. Aquesta és una operació que no podríem fer amb variables ordinals.
5 A diferència de la variable any quan ens referim als anys d’una persona o els anys de durada d’un determinat fenomen. En aquest cas, el zero sí que té significat.
Amb les variables d’interval, però, no podrem calcular la ràtio entre els seus valors, ja que una de les propietats que manca a aquest tipus de variables és que el valor zero no significa «absència de». En l’exemple dels anys del calendari, l’any zero no significa absència de res en concret, com l’absència d’anys o absència de temps. Ho entendrem millor amb un altre exemple: la temperatura en graus Celsius6: els zero graus no representen l’absència de calor ni l’absència de temperatura. Per tant, quan la temperatura puja de 10 a 20 graus, no podrem dir que la calor s’ha duplicat.
6 L’exemple també val per graus Fahrenheit. En canvi, la temperatura en graus Kelvin sí que és una variable de ràtio, ja que el zero indica l’absència de calor i, per tant, passar de 100 a 200 graus Kelvin voldria dir que es duplica la calor.
A R, les variables d’interval s’emmagatzemen preferiblement com a vectors numèrics, encara que en alguns casos les podrem emmagatzemar com a vectors enters o vectors de data.
11.4.1 Operacions amb variables d’interval
Per fer algunes operacions amb variables d’interval hem creat el marc de dades polity, que mostra el nivell de democràcia que tenien diversos països en el seu any de fundació segons la base de dades Polity V (Marshall & Gurr, 2020). Aquesta base de dades assigna un nivell de democràcia als règims polítics entre -10 i 10, on 10 és el nivell màxim de democràcia. El zero, en aquest cas, no significa «absència de», sinó que és un nivell intermedi que adopta un règim polític en aquesta escala7.
7 I encara que l’escala estigués construïda de 0 a 10, el zero tampoc significa «absència de» democràcia.
polity <- tibble(country = c("United States", "Bolivia", "Australia", "Azerbaijan",
"USSR", "Timor Leste", "Eritrea", "Qatar", "Gambia"),
year = c(1776, 1825, 1901, 1991, 1922, 2002, 1993, 1971, 1965),
polity2 = c(0, -3, 10, -3, -7, 6, -6, -10, 8))
polity
## # A tibble: 9 × 3
## country year polity2
## <chr> <dbl> <dbl>
## 1 United States 1776 0
## 2 Bolivia 1825 -3
## 3 Australia 1901 10
## 4 Azerbaijan 1991 -3
## 5 USSR 1922 -7
## 6 Timor Leste 2002 6
## 7 Eritrea 1993 -6
## 8 Qatar 1971 -10
## 9 Gambia 1965 8Amb les operacions que veiem al requadre, podem respondre preguntes com les que fem a continuació:
Quants anys de diferència hi ha entre la fundació dels Estats Units i la fundació de la Unió Soviètica?
polity$year[polity$country == "United States"] - polity$year[polity$country == "USSR"]
## [1] -146En els seus respectius anys de fundació, el nivell de democràcia de Bolívia era més gran que el d’Eritrea?
polity$polity2[polity$country == "Bolivia"] > polity$polity2[polity$country == "Eritrea"]
## [1] TRUEQuins règims polítics tenien nivells de democràcia superiors als Estats Units en el seu any de fundació?
polity$country[polity$polity2[polity$country == "United States"] > polity$polity2]
## [1] "Bolivia" "Azerbaijan" "USSR" "Eritrea" "Qatar"11.4.2 Importar dades d’interval
En la majoria dels casos, les variables d’interval s’importen a R com a vectors numèrics. Ja està bé que s’importin així i no haurem de fer cap transformació addicional. En alguns casos, és fàcil confondre les variables d’interval amb altres tipus de variables, com les ordinals o les de ràtio.
També hem vist anteriorment exemples de bases de dades amb variables d’interval:
- Totes les variables que contenen la variable any, com
yeara les taules taula 10.5, taula 10.4 i taula 10.7. - Variables que mostren una data concreta (
date) a la taula 10.7. - La latitud (
latitude) i la longitud (longitude) de la taula 11.2.
L’eix esquerra-dreta és una de les variables més emprades en Ciència Política. A la taula 11.6, que és un fragment de la Global Party Survey, la veiem a V4_Scale (Norris, 2020). A les enquestes, s’acostuma a preguntar: «Ubiqui’s ideològicament, on 0 és extrema esquerra i 10 extrema dreta». És aquesta una variable d’interval? Òbviament, el zero no té significat, perquè no significa absència d’ideologia, per la qual cosa podem descartar que sigui una variable de ràtio. Fixem-nos que podríem construir una escala on, per exemple, el zero indiqués el centre, -10 l’esquerra i +10 la dreta. O bé que fos 90 dreta i 100 esquerra. Com veiem, una de les propietats de l’escala d’interval és que podem ubicar el principi i el final de l’escala a qualsevol lloc. I això és així perquè el zero no té cap significat i els valors de les escales són completament mòbils i arbitraris.
El que resulta més difícil de dir és si l’autoubicació ideològica és una variable d’interval o ordinal. La principal diferència entre les dues és que a les variables ordinals hi ha una distància coneguda i igual entre els nivells de l’escala. Passar de 4 a 5 a l’eix ideològic hauria de significar el mateix que passar de 5 a 6. I això és qüestionable. Per aquest motiu, alguns autors (veure Johnson et al., 2016, p. 351) defensen que la ideologia és tècnicament una construcció ordinal encara que a la pràctica les escales ordinals construïdes amb nombres es puguin acabar considerant variables d’interval. Una regla no escrita és que si una variable ordinal està formada per set o més valors es pot considerar d’interval (Goertz, 2020 pàg. 139, 144).
| Partyname | Partyabb | V4_Scale | V4_Ord |
|---|---|---|---|
| Brexit Party | BRX | 8.653846 | Strongly economically-right |
| Conservative and Unionist Party | CON | 7.916667 | Strongly economically-right |
| Democratic Unionist Party | DUP | 7.000000 | Center economically-right |
| Green Party | GRN | 2.526316 | Center economically-left |
| Labour Party | Lab | 2.125000 | Strongly economically-left |
| Liberal Democrats | LD | 4.666667 | Center economically-left |
| Plaid Cymru | PC | 3.235294 | Center economically-left |
| Scottish National Party | SNP | 3.162162 | Center economically-left |
| Sinn Féin | SF | 2.708333 | Center economically-left |
| UK Independence Party | UKIP | 8.086956 | Strongly economically-right |
11.4.3 El paquet lubridate
Una de les principals variables d’interval és la de les dates de calendari. Amb això tant ens podem referir a variables com l’any (2013, 2014, 2015…) com a variables més concretes que tinguin com a valors dates exactes (per exemple, «1952-03-10», com hem vist a la variable date de la taula 10.7) o encara més concretes, com seria «1961-01-20 13:00:00». Quan només necessitem l’any com a variable, en tindrem prou amb emmagatzemar-ho com a vector numèric, sense necessitat de fer cap transformació especial. Però a mesura que el temps sigui un factor important del nostre estudi i necessitem jugar amb mesos, setmanes, dies o hores, més important serà utilitzar el paquet lubridate (Spinu et al., 2023).
No entrarem en detall a explicar-lo en aquest mòdul, perquè és un paquet que s’utilitza per necessitats molt concretes. Però hem de saber que ens permet fer operacions com distingir quines dates cauen en cap de setmana, crear nivells ordinals entre dies de la setmana, calcular diferències entre dates o calcular diferències entre franges horàries.
11.5 Variables de ràtio
A diferència de les altres variables que hem vist, les variables numèriques de ràtio (o simplement, variables de ràtio) tenen totes les propietats matemàtiques. Podem dir si els nombres són iguals o diferents, si són més grans o més petits, quina distància hi ha entre ells i també podem saber la quantitat relativa de cada valor. La propietat distintiva de les variables de ràtio és que el zero té significat. Això vol dir que hi ha un punt de referència que marca l’absència del fenomen. El zero en l’edat d’una persona significa absència d’anys, així com el zero en la taxa d’atur significa l’absència d’atur i el zero en població significa que aquell país o territori no té població.
Quan tractem amb variables numèriques, sovint veurem els valors representats amb notació científica:
12000000
## [1] 1.2e+07Interpretar-los és més fàcil del que sembla, ja que simplement hem de moure els decimals tantes vegades a la dreta com ens indiqui l’últim nombre, si és positiu, o tantes vegades a l’esquerra si és negatiu. Per exemple, 2.50+e08 es traduirà com a 250.000.000.
Com que el zero té significat, podem utilitzar-lo per establir relacions entre els valors de la variable a través d’operacions matemàtiques més complexes, com multiplicar, dividir, fer arrels quadrades, etc. Per exemple, podem dir que deu anys són el doble que cinc o que, si l’atur varia del 10 % al 5 %, s’ha reduït a la meitat. Aquestes són operacions que no podem fer amb els altres tipus de variables que hem vist. Per exemple, amb l’escala d’interval de Polity V no podem dir que un país és el doble de democràtic que un altre. Ni tampoc podem dir que un país categoritzat com a «Low Income» sigui la meitat que «Lower Middle Income». Això es deu al fet que el zero, que és un punt real de referència en les variables de ràtio, no existeix ni té significat propi en les altres variables. Des d’un punt de vista de l’anàlisi quantitativa, doncs, les variables de ràtio són preferibles als altres tipus de variables perquè permeten fer més operacions matemàtiques.
A R, emmagatzemarem les variables de ràtio com a vectors numèrics. Algunes d’elles també les podríem emmagatzemar com a vectors enters.
11.5.1 Operacions amb variables de ràtio
Per fer algunes operacions amb variables de ràtio, hem recreat les capacitats materials de les principals potències participants en la Segona Guerra Mundial l’any 1939 a partir de les dades de la National Material Capabilities (NMC) dataset (Singer et al., 1972; Singer, 1987). El marc de dades ratios conté la variable despesa militar (milex, en milers de dòlars), personal militar (milper, en milers), total de població (tpop, en milers), i l’índex CINC (cinc)8, que és una mesura composta que calcula les capacitats materials relatives d’un país en un any determinat.
8 Respon a l’acrònim Composite Index of National Capability. La variable milex respon a la despesa militar, milper a personal militar i tpop a població total. Aquestes i altres variables formen l’índex cinc.
ratio <- tibble(country = c("USA", "UKG", "FRN", "GMY", "ITA", "RUS", "JPN"),
milex = c(980000, 7895671, 1023651, 12000000, 669412, 5984123, 1699970),
milper = c(334, 394, 581, 2750, 581, 1789, 957),
tpop = c(131028, 47762, 41900, 79798, 44020, 170317, 71380),
cinc = c(0.182, 0.0997, 0.0396, 0.178, 0.0270, 0.138, 0.0591))
ratio
## # A tibble: 7 × 5
## country milex milper tpop cinc
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 USA 980000 334 131028 0.182
## 2 UKG 7895671 394 47762 0.0997
## 3 FRN 1023651 581 41900 0.0396
## 4 GMY 12000000 2750 79798 0.178
## 5 ITA 669412 581 44020 0.027
## 6 RUS 5984123 1789 170317 0.138
## 7 JPN 1699970 957 71380 0.0591Amb les operacions que veiem al requadre lateral, podem respondre preguntes com les que fem a continuació:
Amb les variables de ràtio podem fer operacions de:
- Igualtat (
==,%in%) - No igualtat (
!=) - Més gran que (
>) - Més gran o igual que (
>=) - Més petit que (
<) - Més petit o igual que (
<=) - Mínims (
min()) i màxims (max()) - Sumes (
+), restes (-), multiplicacions (*), divisions (/) - Altres tipus d’operacions com arrels quadrades (
sqrt()), logaritmes (log()), màxims (max()), mínims (min()) o mitjanes (mean()).
Quin país té més un personal militar superior al milió de persones?
ratio$country[ratio$milper > 1000]
## [1] "GMY" "RUS"Quantes vegades la despesa militar d’Alemanya és superior cada una de les altres potències?
ratio$milex_gmy <- ratio$milex[ratio$country == "GMY"] / ratio$milexQuin país té un personal militar inferior a l’1 % de la població?
ratio$country[1 > ratio$milper / ratio$tpop * 100]
## [1] "USA" "UKG"Quin és el país amb l’índex CINC més alt?
ratio$country[ratio$cinc == max(ratio$cinc)]
## [1] "USA"Quin és el país amb menys despesa militar?
ratio$country[ratio$milex == min(ratio$milex)]
## [1] "ITA"11.5.2 Importar variables de ràtio
Les variables de ràtio s’acostumen a importar automàticament com a vectors numèrics, que és el que necessitem per poder fer operacions de tot tipus. No obstant això, convé saber distingir entre tres tipus (o ordres) de variables de ràtio: els recomptes, les ràtios i els índexs compostos (Merry, 2016, p. 15; Power, 1999). Aquests tipus de variables els trobem representats a la següent taula 11.7, que inclou dades d’Eurostat i dades de vot a partits regionalistes i independentistes en diverses regions europees (Sanjaume-Calvet et al., n.d.).
| id | country | nuts_name | vote_reg | vote_ind | gdpc | innov | pop | density | area | distance |
|---|---|---|---|---|---|---|---|---|---|---|
| BE1 | Belgium | Région De Bruxelles-Capitale/Brussels Hoofdstedelijk Gewest | 13.81 | 26.31 | 68500 | 135.77406 | 1199095 | 7421.6 | 162 | 0.0384190 |
| BE2 | Belgium | Vlaams Gewest | 0.00 | 43.33 | 39800 | 132.69463 | 6526061 | 487.2 | 13599 | 0.2280460 |
| BE3 | Belgium | Région Wallonne | 4.14 | 0.00 | 28100 | 113.03631 | 3626571 | 215.3 | 16905 | 0.8535276 |
| BG324 | Bulgaria | Разград | 40.08 | 0.00 | 4600 | 34.15538 | 115402 | 47.6 | 2414 | 3.4172388 |
| BG425 | Bulgaria | Кърджали | 63.05 | 0.00 | 3900 | 33.53948 | 150837 | 47.7 | 3212 | 2.4012413 |
| CZ031 | Czech Republic | Jihočeský Kraj | 14.57 | 0.00 | 14800 | 77.76700 | 638782 | 66.5 | 10058 | 0.9911074 |
| CZ032 | Czech Republic | Plzeňský Kraj | 5.80 | 0.00 | 16700 | 77.76700 | 578629 | 77.0 | 7649 | 1.3294820 |
| CZ042 | Czech Republic | Ústecký Kraj | 2.46 | 0.00 | 13100 | 56.43587 | 821377 | 156.9 | 5339 | 0.7669622 |
| CZ071 | Czech Republic | Olomoucký Kraj | 0.75 | 0.00 | 14200 | 75.04677 | 633925 | 121.6 | 5273 | 2.7425572 |
| CZ072 | Czech Republic | Zlínský Kraj | 0.67 | 0.00 | 15600 | 75.04677 | 583698 | 149.2 | 3962 | 3.3911309 |
En aquest capítol, també hem vist anteriorment en bases de dades exemples de variables de ràtio. Per exemple:
- La durada d’una disputa militar militaritzada (duration) a la taula 10.4.
- Els mesos d’un líder polític al càrrec (tenure_months) a la taula 10.8.
- La mida relativa d’un grup ètnic a dins d’un país (size) a la taula 10.6.
Les dades de recompte són dades que compten unitats, com la població (pop) o la superfície del territori (area). Per definició, són dades que les trobarem sense decimals. Les dades de ràtio, en canvi, són les que estan creades a partir de dos nombres. Les més habituals són les dades de percentatge, en què el primer nombre és un recompte i el segon és el total, com les dades de percentatge de vot (vote_reg, que divideix votants a partits regionalistes pel total de votants). Però també ens podem trobar dades de ràtio en la densitat de població (density, compara habitants i àrea) o el PIB per càpita (gdpc, estableix la mitjana d’ingressos per habitant). És molt probable que les dades de ràtio tinguin decimals. Finalment, els índexs són les mesures més complexes, ja que agrupen diverses variables, com per exemple l’Índex d’Innovació Regional (innov).